Практическое
занятие.
ТЕМА:
Интегрирование рациональных дробей.
Внимание! При изучении одного из основных приемов интегрирования: интегрирования рациональных дробей – требуется для проведения строгих доказательств рассматривать многочлены в комплексной области. Поэтому необходимо изучить предварительно некоторые свойства комплексных чисел и операций над ними.
Интегрирование простейших рациональных дробей.
Если P(z) и Q(z) – многочлены в комплексной области, то ![]() - рациональная дробь.
Она называется правильной, если степень P(z) меньше степени Q(z), и неправильной,
если степень Р не меньше степени Q.
- рациональная дробь.
Она называется правильной, если степень P(z) меньше степени Q(z), и неправильной,
если степень Р не меньше степени Q.
Любую
неправильную дробь можно представить в виде:
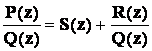 ,
,
где
P(z) = Q(z) S(z)
+ R(z),
a R(z)
– многочлен, степень которого
меньше степени Q(z).
Таким образом, интегрирование рациональных дробей сводится к
интегрированию многочленов, то есть степенных функций, и правильных дробей, так
как ![]() является правильной
дробью.
является правильной
дробью.
Определение 5. Простейшими (или
элементарными) дробями называются дроби следующих видов:
1) ![]() , 2)
, 2) 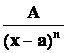 , 3)
, 3) 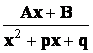 , 4)
, 4) 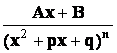
![]() .
.
Выясним, каким образом они интегрируются.
1) ![]()
2) 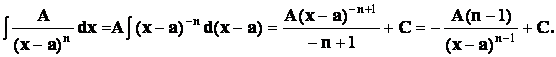
3) 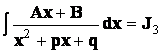 (изучен ранее).
(изучен ранее).
Теорема 5. Всякую правильную дробь
можно представить в виде суммы
простейших дробей (без доказательства).
Следствие 1. Если ![]() - правильная
рациональная дробь, и если среди
корней многочлена
- правильная
рациональная дробь, и если среди
корней многочлена ![]() будут только простые
действительные корни, то в разложении дроби на сумму простейших дробей будет
присутствовать лишь простейшие дроби 1-го типа:
будут только простые
действительные корни, то в разложении дроби на сумму простейших дробей будет
присутствовать лишь простейшие дроби 1-го типа:

Пример
1. 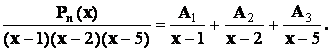
Следствие 2. Если ![]() - правильная
рациональная дробь, и если среди
корней многочлена
- правильная
рациональная дробь, и если среди
корней многочлена ![]() будут только кратные
действительные корни, то в разложении дроби на сумму простейших дробей будет
присутствовать лишь простейшие дроби 1-го и 2-го типов:
будут только кратные
действительные корни, то в разложении дроби на сумму простейших дробей будет
присутствовать лишь простейшие дроби 1-го и 2-го типов:
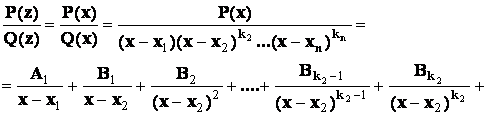
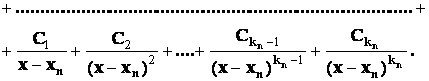
Пример
2. 
Следствие 3. Если ![]() - правильная
рациональная дробь, и если среди
корней многочлена
- правильная
рациональная дробь, и если среди
корней многочлена ![]() будут только простые
комплексно - сопряженные корни, то в разложении дроби на сумму простейших
дробей будет присутствовать лишь простейшие дроби 3-го типа:
будут только простые
комплексно - сопряженные корни, то в разложении дроби на сумму простейших
дробей будет присутствовать лишь простейшие дроби 3-го типа:

Пример
3. 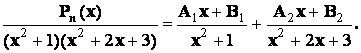
Следствие 4. Если ![]() - правильная
рациональная дробь, и если среди
корней многочлена
- правильная
рациональная дробь, и если среди
корней многочлена ![]() будут только кратные
комплексно - сопряженные корни, то в разложении дроби на сумму простейших
дробей будет присутствовать лишь простейшие дроби 3-го и 4-го типов:
будут только кратные
комплексно - сопряженные корни, то в разложении дроби на сумму простейших
дробей будет присутствовать лишь простейшие дроби 3-го и 4-го типов:
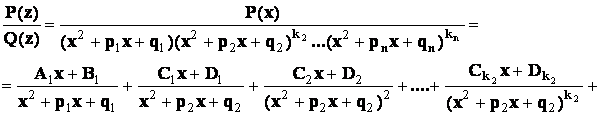
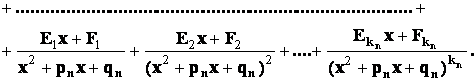
Пример
4.
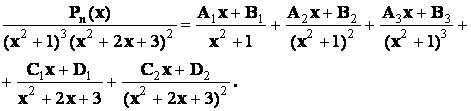
Для определения неизвестных коэффициентов в
приведенных разложениях поступают следующим образом. Левую и правую часть
разложения ![]() , содержащего неизвестные коэффициенты, умножают на
, содержащего неизвестные коэффициенты, умножают на ![]() Получается равенство
двух многочленов. Из него получают уравнения на искомые коэффициенты,
используя, что:
Получается равенство
двух многочленов. Из него получают уравнения на искомые коэффициенты,
используя, что:
1. равенство справедливо при любых значениях Х (метод частных значений). В этом случае получается сколько угодно уравнений, любые m из которых позволяют найти неизвестные коэффициенты.
2. совпадают коэффициенты при одинаковых степенях Х (метод неопределенных коэффициентов). В этом случае получается система m – уравнений с m – неизвестными, из которых находят неизвестные коэффициенты.
3. комбинированный метод.
Пример
5. Разложить дробь 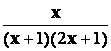 на простейшие.
на простейшие.
Решение: 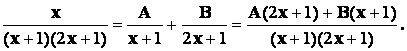
Найдем коэффициенты А и В.
1 способ - метод частных значений:
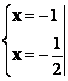
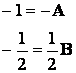
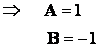
2 способ – метод неопределенных коэффициентов:
![]()
![]()
![]()
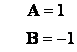
Ответ:
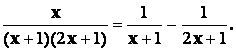
Интегрирование рациональных дробей.
Теорема
6. Неопределенный интеграл от любой рациональной дроби на всяком
промежутке, на котором ее знаменатель не равен нулю, существует и выражается
через элементарные функции, а именно рациональные дроби, логарифмы и
арктангенсы.
Доказательство.
Представим рациональную дробь ![]() в виде:
в виде: 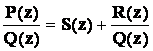 . При этом последнее
слагаемое является правильной дробью, и по теореме 5 ее можно представить в
виде линейной комбинации простейших дробей.
Таким образом, интегрирование рациональной дроби сводится к интегрированию
многочлена S(x) и простейших дробей, первообразные которых, как было
показано, имеют вид, указанный в теореме.
. При этом последнее
слагаемое является правильной дробью, и по теореме 5 ее можно представить в
виде линейной комбинации простейших дробей.
Таким образом, интегрирование рациональной дроби сводится к интегрированию
многочлена S(x) и простейших дробей, первообразные которых, как было
показано, имеют вид, указанный в теореме.
Замечание. Основную трудность при этом
составляет разложение знаменателя на множители, то есть поиск всех его корней.
Пример 1.
Найти интеграл ![]()
Подынтегральная
функция является правильной рациональной дробью. Разложение на неприводимые
сомножители знаменателя имеет вид ![]() Это означает, что
разложение подынтегральной функции в сумму простейших дробей имеет следующий
вид:
Это означает, что
разложение подынтегральной функции в сумму простейших дробей имеет следующий
вид:
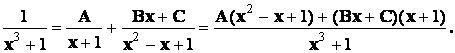
Найдем коэффициенты разложения
комбинированным методом:
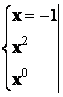
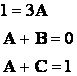
![]()
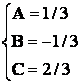
Таким образом,
![]()
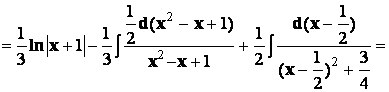
![]()
Пример 2. Найти интеграл 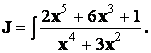
Подынтегральная функция –
неправильная дробь, поэтому выделяем целую часть:

Первый из интегралов – табличный, а второй вычислим
разложением правильной дроби на простейшие:
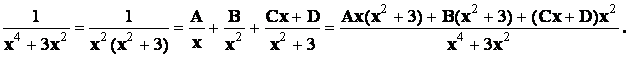
Имеем по методу неопределенных коэффициентов:
![]()
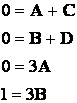
![]()
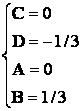
Таким образом,
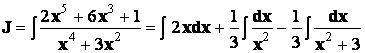
![]()