 |
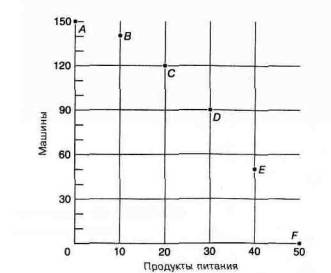
Рис. 1А-1. 6 возможных пар уровней производства «продукты питания-машины»
Перед тем как начать совершенствоваться в экономике, вам понадобится опыт работы с графиками. Они так же необходимы для экономиста, как молоток для плотника. Таким образом, если вы не знакомы с использованием диаграмм, потратьте некоторое время на их изучение, и поверьте, вы не потратите время даром.
Что же такое график Это диаграмма, показывающая, как два или более ряда данных или переменных зависят друг от друга. Графики важны для экономической теории, так как, среди прочего, они позволяют нам анализировать экономические концепции и исследовать исторические тенденции.
В этой книге вы встретитесь со множеством разнообразных графиков. Одни показывают, как переменные меняются во времени, другие показывают зависимость между различными переменными (к рассмотрению этого примера мы сейчас подойдем). Каждый график этой книги поможет вам понять важность экономического закона или тенденции.
Граница производственных возможностей
Первый график, с которым вы встретились в этом тексте, была граница производственных возможностей. Как мы уже упоминали в первой главе, граница производственных возможностей, или PPF, показывает максимальное количество пар товаров или услуг, которое может быть произведено при данных экономических ресурсах, если считать, что все ресурсы полностью задействованы.
Давайте рассмотрим один существенный пример: выбор между производством продуктов питания и машин. В таблице 1А-1 представлены важные для PPF данные, которые близки к примеру, показанному в таблице 1-1. Вспомните, что каждая из возможностей дает один объем производства продуктов питания и один объем производства машин. С увеличением выпуска продуктов питания падает производство машин. Таким образом, если экономическая система производит 10 единиц продуктов питания, то она может сделать максимум 140 машин, но если выпуск пищи равен 20 единицам, то можно произвести только 120 машин.
Таблица 1А-1. Пары возможного выпуска продуктов питания и машин
|
Альтернативные производственные возможности |
||
|
Возможности |
Продукты питания |
Машины |
|
А |
0 |
150 |
|
B |
10 |
140 |
|
C |
20 |
120 |
|
D |
30 |
90 |
|
E |
40 |
50 |
F
|
50 |
0 |
Таблица показывает 6 возможных пар выпуска, которые могут быть получены при данных ресурсах страны. Страна может выбрать одну из 6 возможных комбинаций.
График производственных возможностей
Данные табл. 1А-1 также можно представить в графической форме. Для построения графика мы обозначаем каждую пару данных из табл. 1А-1 точкой на плоскости. Рис. 1А-1 показывает в графической форме отношения между продуктами питания и выпуском машин, представленными в табл. 1А-1. Таким образом, ряд А табл. 1А-1 изображен на рис. 1А-1 как точка А. Аналогичным образом построены точки В, С и т.д.

Рис. 1А-1. 6 возможных пар уровней
производства «продукты питания-машины»
Этот рисунок представляет данные
табл. 1А-1 в графической форме. Данные те же,
но они представлены более наглядно
На рис. 1А-1 вертикальная линяя слева и горизонтальная линяя в нижней части графика соответствуют двум переменным — продуктам питания и машинам. Переменная —это величина, которая может быть определена и измерена, и которая принимает разные значения в зависимости от времени и места. Экономическая теория изучает такие важные переменные как цены, количества, часы работы, акры земли, размер прибыли и т.д.
Горизонтальная прямая графика часто называется горизонтальной осью, или иногда осью X. На рис. 1А-1 выпуск продуктов питания откладывается по горизонтальной оси черного цвета. Вертикальная прямая называется вертикальной осью, или осью Y. На рис. 1А-1 она показывает количество произведенных машин. Точка А вертикальной оси соответствует 150 машинам. Самый нижний левый угол, где встречаются две оси, называется началом координат. Оно соответствует О количеству продуктов питания и 0 количеству машин.
Гладкая кривая. Как показано на рис. 1А-1, для большинства экономических зависимостей характерны как значительные, так и незначительные изменения переменных. Поэтому, обычно мы изображаем экономическую зависимость в виде непрерывной кривой. Рис. 1А-2 показывает PPF как плавную (сглаженную) кривую, в которой соединены точки от А до F.
Сравнивая табл. 1А-1срис. 1А-2, мы
можем понять, почему графики так часто
используются в экономической теории.
Плавная PPF показывает все имеющиеся у
экономики возможности — это наглядный
способ показать, какие виды благ есть в
наличии и в каких количествах. Посмотрев на
рисунок, вы сразу можете увидеть
зависимость между машинами и выпуском продуктов
питания.
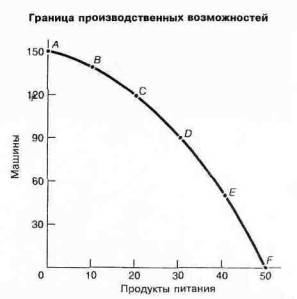
Рис.1А-2
Гладкая кривая проходит через точки, полученные из возможных пар комбинаций, формируя границу производственных возможностей
Рис. 1А-2 показывает зависимость между максимальным объемом производства продуктов питания и производства машин. Один из наиболее важных способ описания зависимостей между двумя переменными — это наклон линии.
Наклон линии показывает изменение одной переменной, происходящее при изменении другой переменной. Точнее — это изменение переменной Y по вертикальной оси на единицу изменения переменной Х по горизонтальной оси. Например, пусть на рис. 1А-2 производство продуктов питания возросло с 25 до 26 единиц. Наклон кривой на рис. 1А-2 точно показывает нам, как изменится производство машин. Наклон — это точный численный критерий зависимости между изменением по Y и по X.
С помощью рис. 1А-3 мы можем показать, как измерять наклон прямой, например, наклон прямой между точками В и D. Представьте себе, что переход от В к D состоит из двух стадий. Первая —это перемещение от В к С, показывающее увеличение на 1 единицу по оси Х (без изменений по Y), а вторая —это компенсирующее перемещение по вертикали вниз или вверх, как показано на рис. 1А-3. (Перемещение по горизонтали на 1 единицу сделано просто для удобства. Формула позволяет перемещаться на любое количество
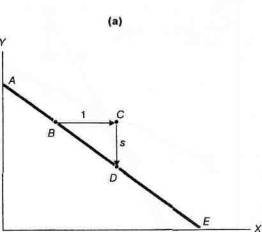
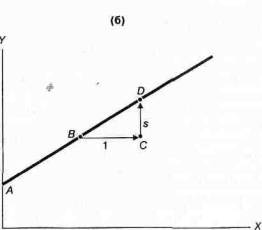
Рис. 1А-3. Расчет наклона прямых
Проще всего вычислять наклон прямых как «подъем при перемещении». Так, и для (а) и для (б) численное значение наклона —это подъем/перемещение=СО/ВС=з/1=з. Отметьте, что в (a) CD отрицательна и соответствует отрицательному наклону или обратной зависимости между Х и Y
единиц). Это двухступенчатое перемещение перенесло нас из одной точки прямой в другую.
Так как перемещение ВС —это увеличение на 1 единицу по X, длина CD (обозначена как s на рис. 1А-3) показывает изменение по Y при изменении на единицу по X. На рисунке это изменение названо наклоном линии ABDE.
Часто наклон определяется как «подъем при перемещении». Подъем — это расстояние по вертикали. На рис. 1 А-3 подъем — это расстояние от С до D. Перемещение—это расстояние по вертикали—ВС на рис. 1А-3. В этом случае подъем при перемещении будет CD над ВС. Таким образом, наклон BD —это CD/BC.
Ниже перечислены наиболее Важные пункты для понимания термина «наклон»:
1. Наклон можно выразить в численном виде. Он показывает изменение по Y при изменении на единицу по Х или «подъем при перемещении».
2. Если линия является прямой, то наклон ее везде постоянен.
3. Наклон линии показывает, какой является зависимость между Х и Y: прямой или обратной. Прямая зависимость имеет место, когда переменные изменяются в одном направлении (т.е. они вместе уменьшаются или увеличиваются). Обратная зависимость существует, если переменные изменя-
|
|
x
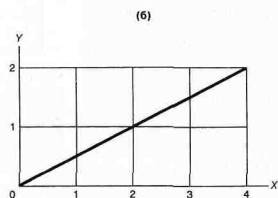
Рис. 1А-4. Крутизна графика отличается от его наклона
Заметьте, что хотя прямая на рис. (а) выглядит более сжатой, чем на рис. (б), они обе показывают одну и ту же зависимость. У обоих графиков наклон равен 1/2, но ось Х графика (б) растянута
ются в противоположных направлениях (т.е. одна возрастает, а другая убывает).
Таким образом, отрицательный наклон показывает, что зависимость между Х и Y обратная, что видно из рис. 1 А -3 (а). Почему же она обратная? Потому, что увеличение по Х вызывает уменьшение по Y.
Люди иногда по внешнему виду путают наклон с крутизной графика. Часто они бывают правы, но не всегда. Крутизна зависит от масштаба графика. Графики (а) и (б) рис. 1А-4 показывают одну и ту же зависимость, но рис. (б) по сравнению с рис. (а) растянут по горизонтальной оси. Если вы сделаете аккуратные подсчеты, то увидите, что наклон прямых одинаков ( и равен 1/2).
Наклон кривой. Кривая или непрямая линия — это линия, у которой меняется наклон. Иногда нам требуется узнать наклон в определенной точке, например в точке В рис. 1А-5. Мы видим, что наклон в точке В положительный, но нам не очень ясно, как его подсчитать.
Для того, чтобы определить наклон плавной кривой в точке, мы должны подсчитать наклон прямой, проходящей по касательной, но не пересекающей кривую в интересующей нас точке. Такая кривая называется касательной к кривой. Иначе говоря, наклон кривой в точке равен наклону прямой, являющейся касательной к данной точке. Если мы изобразим касательную, то мы получим наклон касательной с помощью обычной правоугольной методики измерения, которую мы обсуждали выше.
Для того, чтобы найти наклон в точке В рис. 1А-5, мы должны просто построить прямую FBJ как касательную к кривой в точке В. Затем мы можем подсчитать наклон касательной как NJ/MN. Аналогично, касательная GH дает нам наклон кривой в точке D.
Другой пример наклона кривой показан на рис. 1А-6. Здесь показана типичная микроэкономическая кривая куполообразного вида с максимумом в точке С. Мы можем использовать нашу методику наклонов-как-касательных для того, чтобы увидеть, что наклон всегда положителен в области, где кривая возрастает и отрицателен, где она убывает. На вершине, или на максимуме кривой, наклон равен 0. Нулевой наклон показывает, что небольшой сдвиг переменной по Х относительно максимума не будет влиять на значение переменной по Y*.
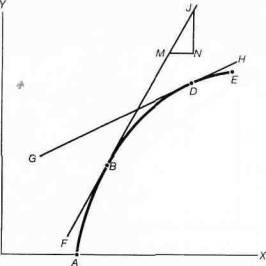
Рис. 1А-5. Касательная как наклон кривой
Построив касательную мы можем подсчитать наклон кривой в данной точке. Таким образом линия FBMJ является касательной к плавной кривой ABD в точке В. Наклон в точке В подсчитывается как наклон касательной, т.е. как NJ/MN
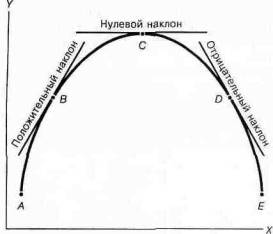
Рис. 1А-6. Различные наклоны кривых
Многие кривые в экономике сначала возрастают, достигают максимума, а затем убывают. От А до С, в области возрастания кривой, наклон ее положителен (см. точку В). В области снижения кривой, от С до Е, наклон ее отрицателен (см. точку D). В точке максимума кривой — точке С, наклон равен 0. (Что же можно сказать об U-об-разной кривой ? Чему равен ее наклон в точке минимума?)
Для тех, кто интересуется алгеброй, мы хотим отметить, что наклон линии можно рассчитать следующим образом: для прямой (или линейной зависимости) — у = а + Ьх наклон кривой равен Ь, который показывает изменение по у, если по х произошло изменение на единицу. Кривая линия или нелинейная зависимость — это зависимость, включающая в себя не только константы и показатель х. Примером нелинейной зависимости может служить квадратное уравнение у=(х-2) .Вы можете быстро удостовериться, что наклон для этого уравнения отрицателен при х<2 и положителен при х>2. Каков же наклон для х=2? .
Сдвиги и движение вдоль кривой
В экономике есть существенное различие между сдвигами кривых и перемещением по ним. Мы можем увидеть их на рис. 1А-7. Лежащая ниже граница производственных возможностей воспроизводит PPF рис. 1А-2. В точке D общество производит 30 единиц продуктов питания и 90 единиц машин. Если общество решит потреблять больше продуктов питания при данной PPF, тогда оно сможет переместиться по кривой к точке Е. Это перемещение показывает, что был сделан выбор в пользу большего производства продуктов питания и меньшего — машин.
Представим себе, что нижняя PPF показывает производственные возможности общества на 1990 год. Если мы вернемся к этой же стране в 2000 году, мы увидим, что PPF сдвинулась от нижней кривой 1990 года к верхней кривой 2000 года. (Этот сдвиг произойдет из-за технического прогресса или из-за того, что ресурсов труда или капитала станет больше.) В последующие годы общество может переместиться на позицию G, где будет производиться больше машин и продуктов питания, по сравнению с D и Е.
Мы привели этот пример с тем, чтобы показать, что в первом случае (переход от D к Е) мы наблюдаем дви-
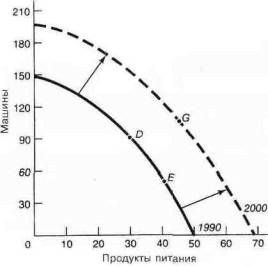
Рис. 1А-7. Сдвиг кривых в сравнении с движением вдоль них.
Используя графики, важно различать движение вдоль кривой (как например от точки с высокими инвестициями D до точки с низкими инвестициями Е) и сдвиг кривой (например от D, точки более ранней по времени, до G — точки, более поздней по времени)
жение вдоль кривой, тогда как во втором случае (от D к G) мы видим сдвиг кривой.
Особые виды графиков
PPF — это пример одного из наиболее важных графиков в экономической теории, который описывает зависимость между двумя экономическими переменными (такими, как продукты питания и машины, или оружие и масло). Ниже вы встретитесь и с другими типами графиков.
Временные ряды. Некоторые графики показывают, как определенные переменные изменяются во времени. На графиках временных рядов по горизонтальной оси откладывается время, по вертикальной оси — интересующие нас переменные (например, коэффициент «государственный долг-ВВП»). Этот график показывает, что процент долга ВВП резко возрастает во время каждой крупной войны.
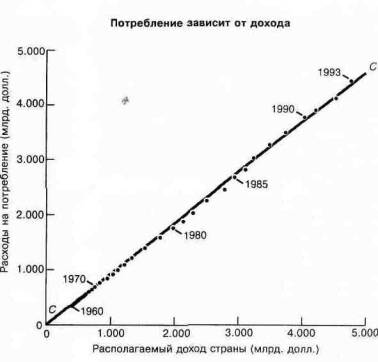
Точечные диаграммы. Иногда отдельные пары точек могут быть нанесены на график так, как показано на рис. 1А-1. Часто на графике показывают комбинации переменных для разных лет. Важный для макроэкономики пример точечной диаграммы — это функция потребления, приведенная на рис. 1А-8. Эта точечная диаграмма показывает общий располагаемый доход страны по горизонтальной оси и общее потребление (расходуемое домашними хозяйствами на блага типа продуктов питания, одежды и жилья) — по вертикальной оси. Обратите внимание, что потребление очень тесно связано с доходом; эта зависимость является ключом к пониманию изменений национального дохода и продукта.
Диаграммы с более чем одной кривой. Часто полезно поместить две кривые на одном графике, и таким образом получить «диаграмму с более чем одной кривой». Наиболее важный пример — это пример диаграммы предложения-спроса, приведенной в главе 3 (см. стр. 89). Графики такого типа могут одновременно показать две различные зависимости: например, как потребитель покупками отвечает на цену (спрос) и как производство отвечает на цену (предложение). Помещая эти зависимости в один график, мы можем определить цену и количество, которые будут держаться на рынке.
На этом мы завершаем наш небольшой экскурс в область графиков. Если вы овладели этими основными принципами, то графики из этой книги и других областей знания могут быть для вас как интересными, так и поучительными.
|
Рис. 1А-8. Точечная диаграмма функции потребления иллюстрирует важный закон макроэкономики Наблюдаемые точки расходов на потребление располагаются вблизи прямой СС, которая показывает усредненную динамику. Так, точка для 1990 года, лежит так близко к линии СС, что по этой линии можно было с точностью, еще до конца года, предсказать ее местоположение. Точечные диаграммы позволяют нам увидеть, насколько тесная зависимость существует между двумя переменными |
РЕЗЮМЕ К ПРИЛОЖЕНИЮ
1. Графики—это важный инструмент для современной экономической теории. Они обеспечивают удобное представление данных или зависимостей между переменными.
2. О графике необходимо знать: что располагается на каждой оси (горизонтальной и вертикальной), каковы единицы каждой оси, какая зависимость показана кривой или кривыми на графике.
3. Зависимость между двумя переменными в кривой показана наклоном. Наклон определяется как подъем при перемещении, или как увеличение по Y при возрастании Х на единицу. Если это возрастающий (положительный) наклон, то две переменных связаны
прямой зависимостью, и они возрастают или убывают вместе. Если на графике представлен убывающий (отрицательный) наклон, то зависимость у двух переменных обратная.
4. Кроме того, иногда мы встречаемся с особыми примерами графиков: временными рядами, которые показывают, как определенные переменные изменяются во времени; точечными диаграммами, которые рассматривают пары переменных; и графиками с несколькими кривыми, в которых рассматриваются две или более зависимостей на одном рисунке.
ОСНОВНЫЕ ПОНЯТИЯ
Элементы графиков
горизонтальная ось, или ось Х.
вертикальная ось, или ось Y
наклон как «подъем при перемещении»
наклон (положительный, отрицательный, нулевой) касательная как наклон кривой
Примеры графиков
графики временных рядов
точечные диаграммы
графики с более чем одной кривой
ВОПРОСЫ ДЛЯ ОБСУЖДЕНИЯ
1. Рассмотрите следующий пример о студенте. После 8 часов сна в день у вас остается 16 часов, которые нужно разделить между отдыхом и учебой. Пусть отдых будет переменной X, а учеба — Y. Постройте на чистом листе бумаги прямую зависимость для всех комбинаций Х и Y. Будьте внимательны при названии осей и отметьте начало координат.
2. Первый вопрос: каков наклон линии, показывающей зависимость между часами учебы и отдыха? Прямая ли это?
3. Пусть вам обязательно требуется 6 часов отдыха в день, не больше и не меньше. На рисунке отметьте точку, соответствующую 6 часам отдыха. Теперь рассмотрите перемещение по прямой: предположите,
что вам нужно только 4 часа отдыха в день. Отметьте новую точку.
4. Теперь покажите сдвиг кривой: пусть вам теперь нужно'меньше сна, и вы можете отвести 18 часов на отдых и учебу. Изобразите новую (смещенную) кривую.
5. В течение недели фиксируйте, сколько часов в день вы сами тратите на отдых и работу. Нарисуйте график временных рядов для часов работы и отдыха каждого дня. Затем изобразите точечную диаграмму для часов работы и отдыха. Видите ли вы какую-нибудь зависимость между двумя переменными?