Вариант №10
Модуль №1. Случайные события
Индивидуальные
задания к модулю №1
10. Урна содержит 5
шаров. Все предложения о числе белых
шаров в урне равновозможные. В урну добавлен белый шар, после чего наудачу взят
один шар. Какова вероятность, что этот шар белый?
20. Завод изготовляет
изделия, каждое из которых с вероятностью 0,1 имеет дефект. В цехе имеются три
контролера; изделие осматривается только одним контролером, с одинаковой
вероятностью первым, вторым или третьим. Вероятность обнаружения дефекта (если
он имеется) для i-гo (i =
l,2,3) контролера равна 0.7, 0.8, 0.9. Если изделие не было забраковано в цехе,
то оно попадает в ОТК завода, где дефект, если он имеется, обнаруживается с
вероятностью 0.95. Определить вероятности следующих событий: А - изделие будет
забраковано; В - изделие будет забраковано в цехе; С - изделие будет
забраковано в ОТК завода.
Модуль №2. Случайные величины
Индивидуальные задания к
модулю № 2
В
задачах 31 - 60 требуется в зависимости от типа случайной величины, который
необходимо определить:
1.
Найти закон распределения
случайной величины x;
2.
Вычислить
числовые характеристики случайной величины (математическое ожидание - Мx, дисперсию - Dx, среднее квадратическое отклонение sx и вероятность принятия значения в заданном интервале - P{xÎ(a;b)};
3.
Построить графики (функции
распределения и для непрерывных случайных величин дифференциальной функции
распределения).
___________________________________________________________________
40.
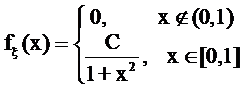 , где С -
константа.
, где С -
константа.
(a = 0,5; b =
0,7).
_____________________________________________________________________
50. x:
|
Хi |
-3 |
2 |
3 |
5 |
8 |
12 |
18 |
20 |
25 |
|
Pi |
2р |
0,1 |
2р |
0,1 |
3р |
0,1 |
4р |
0,1 |
5р |
(a = -1; b = 15).
______________________________________________________________________
60.
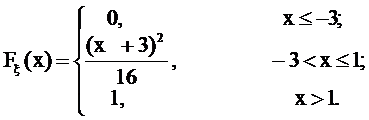 ,
,
(a
= -1; b = 1).
В
задачах 61 - 90 требуется использовать закон больших чисел или его следствия.
70. По условиям
страховки клиенту выплачивается 80$ в
случае травмы и 1000$ в случае смерти.
Застраховано k человек одного возраста.
Известно, что вероятность смерти для данного возраста 0.00001 и вероятность травмы 0.0001.
Определить при каком количестве застрахованных
вероятность получить для страховой компании прибыль менее 500$ будет не менее 0,9, если стоимость
страховки 15$.
80. По условиям
страховки клиенту выплачивается 80$ в
случае травмы и 1000$ в случае смерти.
Застраховано k человек одного возраста.
Известно, что вероятность смерти для данного возраста 0.00001 и вероятность травмы 0.0001.
Определить при каком страховом взносе вероятность убытка для страховой компании
будет не более 0.05.
90. 500 раз подбрасывается
игральная кость. Какова вероятность того, что частота выпадения шестерки
окажется в интервале (1/6-0,05; 1/6+0,05)?
Модуль №3.
Числовые характеристики статистики
Индивидуальные
задания к модулю № 3
Задание к лабораторной
работе 1
В работе, используя выборку, решить следующие задачи:
1. Построить вариационный ряд (дискретный и интервальный);
2. Вычислить относительные частоты (частости) и накопленные частости;
3. Построить графики вариационного ряда ( полигоны и гистограммы относительных и абсолютных частот);
4. Составить эмпирическую функцию распределения, построить ее график;
5. Вычислить числовые характеристики вариационного ряда:
- среднее арифметическое,
- дисперсию,
- стандартное отклонение,
- моду,
- медиану.
Вариант 10
|
57.6 |
54.5 |
53.6 |
57.5 |
54.2 |
56.1 |
53.3 |
54.5 |
57.3 |
54.9 |
|
54.2 |
55.7 |
56 |
55.3 |
52 |
58.7 |
53.8 |
54.8 |
56.4 |
54.2 |
|
50.8 |
52.8 |
55.8 |
56 |
53.1 |
54.1 |
57.6 |
55.5 |
55.9 |
54.5 |
|
56.5 |
54.6 |
57.4 |
54 |
52.1 |
58.5 |
54 |
54.6 |
55.9 |
55.8 |
|
54.7 |
54.1 |
55.8 |
52.3 |
51.6 |
55.5 |
54.3 |
55.3 |
55.1 |
56.7 |
|
56.9 |
55.4 |
55.1 |
55.7 |
52.5 |
54.4 |
56.2 |
55.9 |
55.4 |
53.2 |
|
54.5 |
53.9 |
51.6 |
53.5 |
53.6 |
54.8 |
55.4 |
55.4 |
55.3 |
54.7 |
|
56.2 |
54.2 |
56 |
53.8 |
58.8 |
54.2 |
57 |
55.6 |
53.5 |
58.9 |
|
55.1 |
55 |
55.4 |
55.5 |
52.9 |
56.3 |
54 |
52.5 |
53.9 |
55.7 |
|
55.8 |
53.7 |
53.5 |
53.9 |
55.1 |
51 |
58.2 |
55.6 |
55 |
55 |
Задания к лабораторной
работе 2
В работе, используя выборку, решить следующие задачи:
1.
Вычислить по выборке различные оценки параметра m - среднего значения,
определить наилучшие оценки параметров m - среднего значения, s2
- дисперсии, s
- стандартного отклонения генеральной совокупности ![]() ;
;
2. Найти доверительные интервалы для m при доверительной вероятности b = 0,8; 0,95; 0,99;
3. Считая данные выборки пробными взяв D, полученное при b=0,95, определить минимальный объем выборки n для нахождения доверительного интервала среднего значения - m длины 2D (а также произвольно изменяя D: увеличить и уменьшить) с доверительной вероятностью
b = 0,8; 0,9; 0,95; 0,99; 0,995;
Вариант 6
|
126 |
126 |
125 |
126 |
125 |
125 |
125 |
125 |
125 |
125 |
|
125 |
125 |
125 |
125 |
126 |
125 |
126 |
124 |
125 |
125 |
|
125 |
125 |
125 |
125 |
125 |
125 |
125 |
125 |
125 |
125 |
|
125 |
126 |
126 |
125 |
125 |
125 |
125 |
126 |
125 |
125 |
|
125 |
125 |
126 |
125 |
125 |
125 |
125 |
125 |
125 |
126 |
|
125 |
125 |
124 |
124 |
124 |
125 |
124 |
126 |
126 |
125 |
|
125 |
126 |
125 |
126 |
124 |
125 |
125 |
125 |
125 |
125 |
|
124 |
124 |
126 |
126 |
126 |
125 |
125 |
125 |
125 |
124 |
|
125 |
125 |
125 |
125 |
125 |
125 |
125 |
125 |
125 |
125 |
|
124 |
125 |
124 |
125 |
125 |
125 |
124 |
125 |
126 |
124 |
Модуль №4.
Проверка статистических гипотез
Индивидуальные
задания к модулю № 4
Задания к лабораторной
работе 3
В задачах этой работы используются выборки из генеральных совокупностей с нормальным распределением ХÎN(m,s) (за исключением задачи 3.4).
По данной выборке при уровне значимости a проверить гипотезы в задачах:
3.1. Полагая, что s известно, нужно проверить гипотезу Но: m = mо , а в качестве альтернативной гипотезы можно использовать одну из следующих гипотез Н1: m < mо, Н1: m > mо или Н1: m ¹ mо.
Критическая
область определяется с помощью таблицы «Функции распределения нормированного
нормального распределения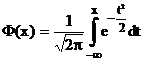 (прил.2). При известном s используем
статистику
(прил.2). При известном s используем
статистику ![]() .
.
Решить задачу, используя выборку
и полученные результаты лабораторной работы 1, mо взять равным
ближайшему целому числу к ![]() , а a = 0,01.
, а a = 0,01.
3.2. Проверить гипотезу: Но:
m
= mо
при Н1: m ¹ mо. При неизвестном s используем
статистику t = ![]() .
.
Критическая область определяется с помощью таблицы «Функции t-распределения Стьюдента с числом степеней свободы n-1», где n-объем выборки.
Вариант 15 ( mо
= 320; ![]() = 0,25; a =
0,005 )
= 0,25; a =
0,005 )
|
320 |
320 |
321 |
320 |
320 |
320 |
320 |
321 |
320 |
320 |
|
320 |
320 |
320 |
320 |
319 |
320 |
320 |
320 |
320 |
319 |
3.3. Проверить гипотезу о дисперсии
нормального распределения ХÎN(m,s). Но: s2 = ![]() при Н1: s2 <
при Н1: s2 < ![]() или Н1: s2
>
или Н1: s2
> ![]() (выбрать подходящую альтернативную
гипотезу).
(выбрать подходящую альтернативную
гипотезу).
Критическая область определяется с помощью таблицы «Функции c2-распределение Пирсона с числом степеней свободы n-1», где n-объем выборки.
3.4. Проверить гипотезу о распределении генеральной совокупности Х. Необходимо по выборке, или учитывая другие соображения, составить гипотезу Но о распределении генеральной совокупности. Для проверки гипотезы использовать c2- критерий согласия Пирсона ( a = 0,05).
Вариант 15
|
3.0 |
4.0 |
1.0 |
0.0 |
2.0 |
3.0 |
0.0 |
1.0 |
1.0 |
0.0 |
|
0.0 |
0.0 |
2.0 |
1.0 |
1.0 |
3.0 |
4.0 |
1.0 |
2.0 |
1.0 |
|
0.0 |
4.0 |
2.0 |
0.0 |
1.0 |
2.0 |
2.0 |
1.0 |
2.0 |
2.0 |
|
1.0 |
8.0 |
2.0 |
1.0 |
3.0 |
1.0 |
1.0 |
2.0 |
1.0 |
1.0 |
|
6.0 |
0.0 |
3.0 |
2.0 |
0.0 |
2.0 |
0.0 |
2.0 |
1.0 |
0.0 |
3.5. Проверить гипотезу о равенстве центров распределения двух нормальных генеральных совокупностей:
а) при известном s используем статистику 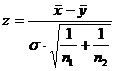 .
.
Критическая область определяется с помощью таблицы функции Ф(х) (прил.2).
б) при неизвестных s1 и s2 , полагая s1 = s2 используем статистику 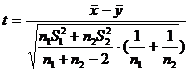 .
.
Критическая область определяется с помощью таблицы «Функции t-распределения Стьюдента с числом степеней свободы n1 + n2 - 2», где n1, n2 -объемы выборок (прил.4) ( a = 0,01; n1 = 20, n2 = 40).
Вариант 15 (s1 = s2 = 2)
X
|
320 |
321 |
321 |
319 |
319 |
322 |
321 |
326 |
321 |
323 |
|
319 |
323 |
321 |
318 |
319 |
319 |
320 |
322 |
319 |
317 |
Y
|
316 |
321 |
321 |
323 |
320 |
321 |
322 |
321 |
320 |
322 |
|
319 |
321 |
320 |
322 |
322 |
320 |
318 |
320 |
320 |
318 |
|
321 |
322 |
320 |
324 |
317 |
320 |
315 |
323 |
322 |
319 |
|
320 |
322 |
320 |
325 |
319 |
322 |
325 |
321 |
322 |
322 |
Модуль №5.
Основы корреляционного и регрессионного анализа
Индивидуальные
задания к модулю № 5
Задание к лабораторной работе 4
В работе приведены результаты наблюдений за парой признаков ( Х,У ). По данным наблюдений требуется:
а) построить
корреляционное поле;
б) найти коэффициент
корреляции между признаками Х и У;
в) найти уравнение
линейной регрессии у = f(x)
и дать объяснение полученному результату, используя экономический смысл данных;
г) нанести график
прямой регрессии на корреляционное поле и сделать предварительный прогноз.
Вариант 13 (Х - среднесписочный состав работников (чел.); У - розничный товарооборот (усл. ед.))
|
Х |
172 |
99 |
148 |
104 |
144 |
110 |
134 |
116 |
129 |
125 |
|
У |
35.2 |
14.1 |
26.4 |
16.3 |
25.1 |
17.8 |
23.2 |
19.1 |
21.5 |
19.7 |
|
Х |
91 |
154 |
104 |
144 |
107 |
137 |
113 |
130 |
124 |
126 |
|
У |
12.5 |
28.1 |
15.6 |
25.7 |
17.4 |
23.5 |
18.2 |
21.6 |
19.5 |
20.4 |
|
Х |
159 |
101 |
146 |
105 |
142 |
112 |
133 |
121 |
129 |
125 |
|
У |
28.5 |
14.6 |
26.2 |
16.5 |
24.8 |
18.0 |
21.7 |
19.2 |
21.1 |
20.0 |
|
Х |
96 |
150 |
104 |
144 |
107 |
136 |
115 |
130 |
124 |
125 |
|
У |
13.5 |
26.7 |
16.2 |
25.5 |
17.6 |
23.4 |
18.7 |
21.6 |
19.5 |
20.0 |
|
Х |
159 |
102 |
144 |
105 |
142 |
112 |
132 |
123 |
129 |
126 |
|
У |
28.2 |
15.5 |
25.8 |
16.8 |
24.5 |
18.2 |
21.6 |
19.4 |
20.5 |
20.2 |