Вариант №2

Модуль №1. Случайные события

Индивидуальные задания к модулю №1

 

2. Цена на продукцию некоторого предприятия снижается в течение некоторого периода три раза. Потом, если она не будет реализована, ее необходимо уничтожить так как она приходит в негодность. Вероятность продажи до снижения цены равна 0,85, а после каждого снижения она уменьшалась на 0,15. Найти вероятность того, что:

a)   продукция не будет реализована;

b)  будет реализована;

c)  будет реализована хотя бы при одном снижении.

 

22. Вероятность возникновения опасной для прибора перегрузки в каждом опыте равна 0,4. Определить вероятность отказа прибора в серии из трех независимых опытов.

 

Модуль №2. Случайные величины

Индивидуальные задания к модулю № 2

 

В задачах 31 - 60 требуется в зависимости от типа случайной величины, который необходимо определить:

1.  Найти закон распределения случайной величины x;

2.  Вычислить числовые характеристики случайной величины (математическое ожидание - Мx, дисперсию - Dx, среднее квадратическое отклонение sx и вероятность принятия значения в заданном интервале - P{xÎ(a;b)};

3.  Построить графики (функции распределения и для непрерывных случайных величин дифференциальной функции распределения).

___________________________________________________________________

32.

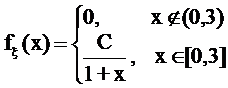         ,          где С - константа.

                                                                  (a = 1; b = 2).

_____________________________________________________________________

42. x = h - z, если

 

h:                                  z:

Уi

-1

0

1

2

Pi

0,2

0,3

P3

0,1

 

Zi

-2

-1

0

1

Pi

0,1

0,3

P3

0,4

                                                       

                                                                  (a = -1; b = 1).

______________________________________________________________________

52. x = h х z, если

 

h:                        z:

Уi

-1

0

1

Pi

0,2

P2

0,4

 

Zi

-2

-1

0

Pi

0,1

0,3

P3

 

                                                                  (a = -2; b = 1).

 

 

В задачах 61 - 90 требуется использовать закон больших чисел или его следствия.

 

 

62. Оценить вероятность  для k = l,2,3, если случайная величина x, подчинена нормальному закону N(5,2). Сравнить с точными значениями этих вероятностей.

 

72. По условиям страховки клиенту выплачивается 100$ в случае травмы и 1000$ в случае смерти. Застраховано 400 человек одного возраста. Известно, что вероятность смерти для данного возраста 0.00001 и вероятность травмы 0.0001. Найти вероятность того, что прибыль страховой компании составит не менее 500$, если стоимость страховки 10$.

 

82. В некотором районе г. Донецка имеется 5000 квартир. Вероятность того, что произойдет пожар в квартире равна 0,0002. Найти наивероятнейшее число пожаров и вероятность этого числа пожаров.

 

Модуль №3. Числовые характеристики статистики

Индивидуальные задания к модулю № 3

 

Задание к лабораторной работе 1

 

            В работе, используя выборку, решить следующие задачи:

1. Построить вариационный ряд (дискретный и интервальный);

2. Вычислить относительные частоты (частости) и накопленные частости;

3. Построить графики вариационного ряда ( полигоны и гистограммы относительных и абсолютных частот);

4. Составить эмпирическую функцию распределения, построить ее график;

5. Вычислить числовые характеристики вариационного ряда:

- среднее арифметическое,

- дисперсию,

- стандартное отклонение,

- моду,

- медиану.

Вариант 2

26.7

24.6

24.6

25.4

25.1

25.3

24.8

25.8

26

23.6

24.9

26.8

25.5

24.6

24.9

25.9

25.3

23.3

25.3

23.6

28.1

24.4

23.7

26.4

24.6

25.2

27.4

24.4

25.7

24.4

26.4

25.6

24.6

27.1

24.1

24.5

25.1

21.2

23.8

25.8

23.3

24.1

27.2

25.5

25.7

22.4

25.3

25.5

25.2

26.8

22.7

25.8

23.7

25.7

25.9

24.5

25.7

25

25.4

25.4

25.4

23

23.6

27.8

26.2

27.3

26.5

25.7

24.7

26.5

25.6

24.5

26.2

25.5

23.3

24

23.9

26.6

21.9

25.1

24.4

26

24.9

27.7

23

24.8

26.2

23.9

26.1

27.2

24.6

24.5

24.9

25.3

24.5

24.5

25.4

23.9

25.3

24.1

 

 

Задания к лабораторной работе 2

           

В работе, используя выборку, решить следующие задачи:

            1. Вычислить по выборке различные оценки параметра m - среднего значения, определить наилучшие оценки параметров m - среднего значения, s2 - дисперсии, s - стандартного отклонения генеральной совокупности ;

2. Найти доверительные интервалы для m при доверительной вероятности b = 0,8; 0,95; 0,99;

            3. Считая данные выборки пробными взяв D, полученное при b=0,95, определить минимальный объем выборки n для нахождения доверительного интервала среднего значения - m длины 2D  (а также произвольно изменяя D: увеличить и уменьшить) с доверительной  вероятностью

 b = 0,8; 0,9; 0,95; 0,99; 0,995;

 

Вариант 14

344

344

350

347

344

346

342

343

342

347

347

345

349

345

343

345

348

344

347

351

345

350

349

346

346

344

348

344

345

347

347

342

346

349

345

349

346

345

345

340

346

346

347

346

346

343

343

348

350

345

346

349

347

351

349

343

343

346

346

343

343

347

343

347

347

341

342

345

345

346

345

347

344

344

346

347

348

349

341

342

344

346

342

348

345

345

345

347

345

344

346

349

344

343

347

348

344

343

347

343

 

 

Модуль №4.  Проверка статистических гипотез

Индивидуальные задания к модулю № 4

 

Задания к лабораторной работе 3

 

            В задачах этой работы используются выборки из генеральных совокупностей с нормальным распределением ХÎN(m,s)  (за исключением задачи 3.4).

            По данной выборке при уровне значимости a проверить гипотезы в задачах:

 

            3.1. Полагая, что s известно, нужно проверить гипотезу Но: m = mо , а в качестве альтернативной гипотезы можно использовать одну из следующих гипотез Н1: m < mо, Н1: m > mо или Н1: m ¹ mо.

            Критическая область определяется с помощью таблицы «Функции распределения нормированного нормального распределения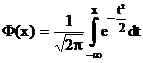 (прил.2). При известном s используем статистику .

Решить задачу, используя выборку и полученные результаты лабораторной работы 1, mо  взять равным ближайшему целому числу к , а a = 0,01.

 

           

3.2. Проверить гипотезу: Но: m = mо при Н1: m  ¹ mо. При неизвестном s используем статистику   t = .

            Критическая область определяется с помощью таблицы «Функции t-распределения Стьюдента с числом степеней свободы n-1», где n-объем выборки.

 

Вариант 10. ( mо = 250;   = 4; a = 0,01)

252

247

252

248

249

250

250

251

250

247

247

254

245

251

250

248

252

247

249

251

 

 

 

            3.3. Проверить гипотезу о дисперсии нормального распределения ХÎN(m,s). Но: s2 =  при Н1: s2 <  или Н1: s2 >  (выбрать подходящую альтернативную гипотезу).

            Критическая область определяется с помощью таблицы «Функции c2-распределение Пирсона с числом степеней свободы n-1», где n-объем выборки.

 

 

            3.4. Проверить гипотезу о распределении генеральной совокупности Х. Необходимо по выборке, или учитывая другие соображения, составить гипотезу Но о распределении генеральной совокупности. Для проверки гипотезы использовать c2- критерий согласия Пирсона.

 

Вариант 10

 

452

449

450

448

452

449

448

452

451

451

454

448

449

449

449

451

451

451

451

450

454

450

452

454

455

452

450

449

450

446

448

448

450

449

450

451

448

448

454

451

452

451

449

449

450

453

453

449

447

449

 

3.5. Проверить гипотезу о равенстве центров распределения двух нормальных генеральных совокупностей:

а) при известном s используем статистику .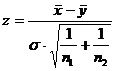

            Критическая область определяется с помощью таблицы функции Ф(х) (прил.2).

 

б) при неизвестных s1 и s2 , полагая s1 = s2  используем статистику .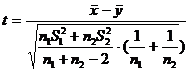

            Критическая область определяется с помощью таблицы «Функции t-распределения Стьюдента с числом степеней свободы n1 + n2 - 2», где n1, n2 -объемы выборок (прил.4).

 

Вариант 10 (s1 = s2 = 2) ( a = 0,01; n1 = 20, n2 = 40)

 X

14.0

19.8

22.2

22.2

20.7

22.9

19.8

20.1

18.7

22.3

19.0

17.0

18.4

20.1

18.1

22.0

19.0

18.2

22.2

23.6

Y

20.4

18.0

19.3

20.6

20.1

19.8

24.1

18.0

18.5

20.7

18.4

20.0

19.3

19.9

22.2

19.1

17.0

19.5

22.9

22.4

17.8

18.8

23.2

21.5

20.9

17.8

21.9

23.7

18.0

22.8

19.5

18.7

20.3

17.5

24.2

20.8

18.8

18.3

19.4

18.5

 

Модуль №5.  Основы корреляционного и регрессионного анализа

Индивидуальные задания к модулю № 5

 

Задание к лабораторной работе 4

 

            В работе приведены результаты наблюдений за парой признаков ( Х,У ). По данным наблюдений требуется:

            а) построить корреляционное поле;

            б) найти коэффициент корреляции между признаками Х и У;

            в) найти уравнение линейной регрессии у = f(x) и дать объяснение полученному результату, используя экономический смысл данных;

            г) нанести график прямой регрессии на корреляционное поле и сделать предварительный прогноз.

 

Вариант 5 (Х - объем выполненных работ (усл. ед.);  У - накладные расходы  (усл. ед.))

 

Х

45.2

52.8

47.0

51.7

48.2

50.8

48.6

50.1

49.1

У

450

541

471

522

479

518

484

512

490

Х

53.3

46.8

51.9

47.9

51.2

48.4

50.4

49.0

49.8

У

548

466

529

476

520

480

513

488

510

Х

45.8

52.0

47.6

51.4

48.3

50.6

48.9

50.0

49.2

У

451

538

472

522

480

517

485

512

494

Х

53.2

47.0

51.8

48.0

51.0

48.4

50.4

49.0

49.8

У

546

468

529

478

520

482

512

490

507

Х

46.5

51.9

47.8

51.3

48.4

50.6

49.0

50.0

49.3

У

453

531

474

521

480

513

487

510

494