Вариант №4

Модуль №1. Случайные события

Индивидуальные задания к модулю №1

4. Электролампы упакованы по 10 штук в ящике. Все предложения о числе бракованных ламп в ящике равновозможные. В ящик добавили одну стандартную лампу, после чего наудачу взята одна лампа. Какова вероятность, что она стандартна?

24. Трое поочередно бросают монету. Выигрывает тот, у которого раньше выпадает «герб». Определить вероятность выигрыша для каждого из игроков.

Модуль №2. Случайные величины

Индивидуальные задания к модулю № 2

В задачах 31 - 60 требуется в зависимости от типа случайной величины, который необходимо определить:

1. Найти закон распределения случайной величины x;

2. Вычислить числовые характеристики случайной величины (математическое ожидание - Мx, дисперсию - Dx, среднее квадратическое отклонение sx и вероятность принятия значения в заданном интервале - P{xÎ(a;b)};

3. Построить графики (функции распределения и для непрерывных случайных величин дифференциальной функции распределения).

___________________________________________________________________

34. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого в одном опыте = 0.1. x - число отказавших элементов в одном опыте. (a = 1; b = 2). Дополнительно к указанным выше заданиям выполнить: а) построить ряд распределения; б) построить многоугольник распределения.

_____________________________________________________________________

44. x:

Хi	x1	x2	9	12	15
Pi	0,2	P2	0,2	0,4	0,1

если Мx = 9,3; Dx = 15,21, (a =5; b =11).

______________________________________________________________________

54. Рабочий обслуживает 4 станка. Вероятность того, что в течении часа станок не потребует внимания рабочего равна для первого станка 0.7, для второго - 0.75, для третьего - 0.8, для четвертого 0.9. x - число станков, которые не потребуют внимания рабочего в течение часа. (a = 1; b = 3).

В задачах 61 - 90 требуется использовать закон больших чисел или его следствия.

64. Вероятность рождения мальчика равна 0.515. Оценить снизу вероятность того, что число девочек среди 1000 новорожденных будет отличаться от математического ожидания этого числа по абсолютной величине менее, чем на 20.

74. Завод отправил на базу 2000- изделий. Вероятность поврежден каждого из изделий в пути равна 0,003 . Найти вероятность того, что пути будет повреждено менее трех изделий и определить вероятность найвероят-нейшего числа не поврежденных изделий.

84. Страховая компания застраховала 5000 квартир на случай пожара на сумму 2000 гривен каждую. Вероятность пожара с таким ущербом равна 0,0003. Определить (используя предельную теорему) вероятность того, что сумма платежей не превысит 100.000 долларов.

Модуль №3. Числовые характеристики статистики

Индивидуальные задания к модулю № 3

Задание к лабораторной работе 1

В работе, используя выборку, решить следующие задачи:

1. Построить вариационный ряд (дискретный и интервальный);

2. Вычислить относительные частоты (частости) и накопленные частости;

3. Построить графики вариационного ряда ( полигоны и гистограммы относительных и абсолютных частот);

4. Составить эмпирическую функцию распределения, построить ее график;

5. Вычислить числовые характеристики вариационного ряда:

- среднее арифметическое,

- дисперсию,

- стандартное отклонение,

- моду,

- медиану.

Вариант 4

81.8	80.2	81.4	77.5	80.6	81.7	80.5	77.3	80.1	80.7
77.8	80.3	80.9	80.4	80.8	80.7	77.7	77.3	77.9	80.8
80.2	83.4	80	74.9	80.5	78.3	81.2	78.5	82.7	80.7
78.4	83.1	81.3	78.4	79.2	79.2	78.8	79.2	77.6	82.8
80.3	79.8	83.9	79.3	76.9	83.5	82.4	79.3	77.2	80.6
81.3	80.1	79.1	79.5	79.2	80.2	80.6	76	83	80.6
79	78.9	80.2	78.6	80.4	81.8	78.4	80.4	79.8	79.1
80.5	80.6	79.4	80.6	77.3	80.6	79	78.2	79	78.5
79.3	80.4	83	82.2	80	84.5	84.4	80.5	78.4	78.1
79.2	76.6	77.4	79.6	79.3	78.7	78.9	79.1	78.4	79.4

Задания к лабораторной работе 2

В работе, используя выборку, решить следующие задачи:

1. Вычислить по выборке различные оценки параметра m - среднего значения, определить наилучшие оценки параметров m - среднего значения, s² - дисперсии, s - стандартного отклонения генеральной совокупности ;

2. Найти доверительные интервалы для m при доверительной вероятности b = 0,8; 0,95; 0,99;

3. Считая данные выборки пробными взяв D, полученное при b=0,95, определить минимальный объем выборки n для нахождения доверительного интервала среднего значения - m длины 2D (а также произвольно изменяя D: увеличить и уменьшить) с доверительной вероятностью

b = 0,8; 0,9; 0,95; 0,99; 0,995;

Вариант 12

143	144	145	144	145	145	144	146	146	146
146	146	144	145	143	144	145	146	145	145
147	146	144	146	146	145	145	145	145	145
144	144	144	144	145	146	145	145	145	145
144	145	144	147	146	145	145	144	145	144
144	144	144	145	145	146	145	145	146	145
144	145	145	145	144	144	144	144	146	146
146	146	146	145	145	147	143	147	146	144
145	145	145	146	146	145	146	145	145	148
144	146	144	145	145	145	143	146	146	147

Модуль №4. Проверка статистических гипотез

Индивидуальные задания к модулю № 4

Задания к лабораторной работе 3

В задачах этой работы используются выборки из генеральных совокупностей с нормальным распределением ХÎN(m,s) (за исключением задачи 3.4).

По данной выборке при уровне значимости a проверить гипотезы в задачах:

3.1. Полагая, что s известно, нужно проверить гипотезу Н_о: m = m_о , а в качестве альтернативной гипотезы можно использовать одну из следующих гипотез Н₁: m < m_о, Н₁: m > m_о или Н₁: m ¹ m_о.

Критическая область определяется с помощью таблицы «Функции распределения нормированного нормального распределения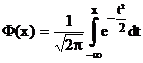 (прил.2). При известном s используем статистику .

Решить задачу, используя выборку и полученные результаты лабораторной работы 1, m_о взять равным ближайшему целому числу к , а a = 0,01.

3.2. Проверить гипотезу: Н_о: m = m_о при Н₁: m ¹ m_о. При неизвестном s используем статистику t = .

Критическая область определяется с помощью таблицы «Функции t-распределения Стьюдента с числом степеней свободы n-1», где n-объем выборки.

Вариант 6. ( m_о = 135; = 9; a = 0,002 ).

134	138	133	137	133	137	133	131	139	133
133	138	133	135	133	140	130	131	133	135

3.3. Проверить гипотезу о дисперсии нормального распределения ХÎN(m,s). Н_о: s² = при Н₁: s² < или Н₁: s² > (выбрать подходящую альтернативную гипотезу).

Критическая область определяется с помощью таблицы «Функции c²-распределение Пирсона с числом степеней свободы n-1», где n-объем выборки.

3.4. Проверить гипотезу о распределении генеральной совокупности Х. Необходимо по выборке, или учитывая другие соображения, составить гипотезу Н_о о распределении генеральной совокупности. Для проверки гипотезы использовать c²- критерий согласия Пирсона ( a = 0,05).

Вариант 6

50.03	65.29	68.46	63.58	67.50	64.99	61.13	70.17	58.17	63.97
54.24	71.51	59.65	50.46	74.53	63.60	67.75	73.17	55.08	72.10
58.42	68.95	64.43	55.47	61.36	67.88	54.55	51.85	72.67	55.73
56.45	57.70	71.90	53.42	64.95	64.18	71.15	55.50	66.49	64.44
71.27	56.09	51.26	57.64	52.86	66.41	63.79	63.03	62.33	72.46

3.5. Проверить гипотезу о равенстве центров распределения двух нормальных генеральных совокупностей:

а) при известном s используем статистику .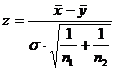

Критическая область определяется с помощью таблицы функции Ф(х) (прил.2).

б) при неизвестных s₁ и s₂ , полагая s₁ = s₂ используем статистику .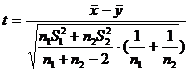

Критическая область определяется с помощью таблицы «Функции t-распределения Стьюдента с числом степеней свободы n₁ + n₂ - 2», где n₁, n₂ -объемы выборок (прил.4) ( a = 0,01; n₁ = 20, n₂ = 40).

Вариант 6 (s₁ = s₂ = 3)

X

118	120	122	118	119	117	124	119	124	121
126	115	115	122	120	122	116	122	122	116

Y

117	121	116	118	119	117	121	118	126	117
122	121	117	124	114	123	122	117	122	118
116	122	120	117	117	118	123	123	114	123
125	120	112	121	120	122	129	115	123	120

Модуль №5. Основы корреляционного и регрессионного анализа

Индивидуальные задания к модулю № 5

Задание к лабораторной работе 4

В работе приведены результаты наблюдений за парой признаков ( Х,У ). По данным наблюдений требуется:

а) построить корреляционное поле;

б) найти коэффициент корреляции между признаками Х и У;

в) найти уравнение линейной регрессии у = f(x) и дать объяснение полученному результату, используя экономический смысл данных;

г) нанести график прямой регрессии на корреляционное поле и сделать предварительный прогноз.

Вариант 7 (Х - энерговооруженность (относ. ед.); У - себестоимость продукции (усл. ед.))

Х	74	60	69	61	68	62	67	64	66
У	583	697	619	680	630	674	635	666	643
Х	57	70	61	68	62	67	63	66	64
У	707	608	685	626	678	633	670	641	656
Х	73	61	69	62	68	62	67	64	66
У	587	690	623	679	630	671	635	660	643
Х	60	70	61	68	62	67	63	66	65
У	698	618	681	629	675	634	670	642	655
Х	70	61	68	62	67	63	67	64	65
У	604	687	625	679	631	670	639	657	647