Вариант №7

Модуль №1. Случайные события

Индивидуальные задания к модулю №1

7. Устройство содержит три независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,04; 0,05 и 0,06. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказали:

а) хотя бы два элемента; b) хотя бы один элемент.

27. В игре «Спортлото 5 из 36» участник наудачу зачеркивает 5 из 36 чисел, написанных на игровом поле. Найти вероятность того, что в результате тиража будет угадано: а) три числа; b) четыре числа; c) все пять чисел;

Модуль №2. Случайные величины

Индивидуальные задания к модулю № 2

В задачах 31 - 60 требуется в зависимости от типа случайной величины, который необходимо определить:

1. Найти закон распределения случайной величины x;

2. Вычислить числовые характеристики случайной величины (математическое ожидание - Мx, дисперсию - Dx, среднее квадратическое отклонение sx и вероятность принятия значения в заданном интервале - P{xÎ(a;b)};

3. Построить графики (функции распределения и для непрерывных случайных величин дифференциальной функции распределения).

___________________________________________________________________

37.

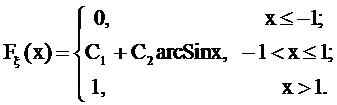, где С₁,C₂ - константы.

(a = 0; b = 1/2).

_____________________________________________________________________

47.

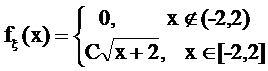, где С - константа.

(a = -2; b = 3).

______________________________________________________________________

57. x:

Хi	x1	x2	20	25	30
Pi	0,1	0,2	P3	0,2	0,4

если Мx = 22,4; Dx = 62,04, (a =5; b =11).

В задачах 61 - 90 требуется использовать закон больших чисел или его следствия.

67. Определить, имеет ли место закон больших чисел для попарно независимых случайных величин {x_n}, (n=1,2,3,...) заданных рядами распределения:

хi	-na	0	-na
рi

77. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 250 деталей не больше двух бракованных и вероятность, что число стандартных изделий будет заключено в приделах 150-200.

87. Среднесуточное потребление электроэнергии в населенном пункте равно 12000 квт. ч. Оценить вероятность того, что потребление электроэнергии в этом населенном пункте в течение данных суток превзойдет 50000 квт. ч.

Модуль №3. Числовые характеристики статистики

Индивидуальные задания к модулю № 3

Задание к лабораторной работе 1

В работе, используя выборку, решить следующие задачи:

1. Построить вариационный ряд (дискретный и интервальный);

2. Вычислить относительные частоты (частости) и накопленные частости;

3. Построить графики вариационного ряда ( полигоны и гистограммы относительных и абсолютных частот);

4. Составить эмпирическую функцию распределения, построить ее график;

5. Вычислить числовые характеристики вариационного ряда:

- среднее арифметическое,

- дисперсию,

- стандартное отклонение,

- моду,

- медиану.

Вариант 7

17.6	20.1	21.2	25.2	20.4	19.7	19.1	21.5	22.5	19.2
20.7	20.8	16.3	18.8	25	19.1	19.7	16.9	15.6	22.1
22.2	26.9	19	22.6	21.5	15.5	18	18	15.5	21
22.4	18	17.7	15.8	19.2	15.4	18.9	20.2	24.4	17.4
23.2	18.5	18.1	20.3	17.1	22.9	22.6	18.4	20.8	22.3
13.9	14.2	23.2	20.2	18.6	16.1	19.3	17.4	20.8	23.4
22.5	21.7	19.9	22.1	18.2	17.3	18.9	26.2	19.4	22.1
24.5	19.4	20.6	23.3	18.8	22.3	24.5	24.9	21.5	21.3
20.6	18.6	15.8	16.4	25.4	23.9	19.1	19.9	16.4	19.2
20.2	18	20.3	22.6	20.7	24.7	17.8	18.3	23.3	22

Задания к лабораторной работе 2

В работе, используя выборку, решить следующие задачи:

1. Вычислить по выборке различные оценки параметра m - среднего значения, определить наилучшие оценки параметров m - среднего значения, s² - дисперсии, s - стандартного отклонения генеральной совокупности ;

2. Найти доверительные интервалы для m при доверительной вероятности b = 0,8; 0,95; 0,99;

3. Считая данные выборки пробными взяв D, полученное при b=0,95, определить минимальный объем выборки n для нахождения доверительного интервала среднего значения - m длины 2D (а также произвольно изменяя D: увеличить и уменьшить) с доверительной вероятностью

b = 0,8; 0,9; 0,95; 0,99; 0,995;

Вариант 9

552	549	549	552	550	552	549	549	550	549
550	550	550	547	550	551	551	550	549	552
547	550	551	552	549	551	550	550	551	549
552	550	550	552	548	549	549	551	551	550
549	549	549	549	550	547	548	549	552	554
551	549	551	549	549	550	552	548	549	550
551	549	549	550	551	549	551	550	552	550
549	549	551	551	550	550	549	550	550	550
551	547	548	552	551	550	551	550	550	551
551	552	551	549	551	547	550	551	548	549

Модуль №4. Проверка статистических гипотез

Индивидуальные задания к модулю № 4

Задания к лабораторной работе 3

В задачах этой работы используются выборки из генеральных совокупностей с нормальным распределением ХÎN(m,s) (за исключением задачи 3.4).

По данной выборке при уровне значимости a проверить гипотезы в задачах:

3.1. Полагая, что s известно, нужно проверить гипотезу Н_о: m = m_{о ,} а в качестве альтернативной гипотезы можно использовать одну из следующих гипотез Н₁: m < m_о, Н₁: m > m_о или Н₁: m ¹ m_о.

Критическая область определяется с помощью таблицы «Функции распределения нормированного нормального распределения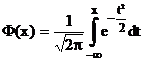 (прил.2). При известном s используем статистику .

Решить задачу, используя выборку и полученные результаты лабораторной работы 1, m_о взять равным ближайшему целому числу к , а a = 0,01.

3.2. Проверить гипотезу: Н_о: m = m_о при Н₁: m ¹ m_о. При неизвестном s используем статистику t = .

Критическая область определяется с помощью таблицы «Функции t-распределения Стьюдента с числом степеней свободы n-1», где n-объем выборки.

Вариант 13. ( m_о = 12; = 9; a = 0,02 )

10.02	13.63	11.90	11.89	11.57	5.88	13.96	13.12	8.21	8.80
10.55	12.96	11.26	9.67	15.64	12.78	14.98	17.05	14.19	11.04

3.3. Проверить гипотезу о дисперсии нормального распределения ХÎN(m,s). Н_о: s² = при Н₁: s² < или Н₁: s² > (выбрать подходящую альтернативную гипотезу).

Критическая область определяется с помощью таблицы «Функции c²-распределение Пирсона с числом степеней свободы n-1», где n-объем выборки.

3.4. Проверить гипотезу о распределении генеральной совокупности Х. Необходимо по выборке, или учитывая другие соображения, составить гипотезу Н_о о распределении генеральной совокупности. Для проверки гипотезы использовать c²- критерий согласия Пирсона ( a = 0,05).

Вариант 13

51	58	61	51	61	54	58	55	48	56
60	49	52	48	48	55	50	48	55	50
55	54	57	52	52	51	50	49	53	46
50	51	56	42	54	54	52	56	49	50
43	41	53	50	58	53	50	47	51	52

3.5. Проверить гипотезу о равенстве центров распределения двух нормальных генеральных совокупностей:

а) при известном s используем статистику .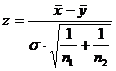

Критическая область определяется с помощью таблицы функции Ф(х) (прил.2).

б) при неизвестных s₁ и s₂ , полагая s₁ = s₂ используем статистику .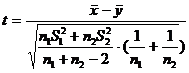

Критическая область определяется с помощью таблицы «Функции t-распределения Стьюдента с числом степеней свободы n₁ + n₂ - 2», где n₁, n₂ -объемы выборок (прил.4) ( a = 0,01; n₁ = 20, n₂ = 40).

Вариант 13 (s₁ = s₂ = 1.5)

X

30.74	29.82	29.77	30.51	31.29	28.79	30.45	30.55	31.72	30.65
28.50	31.72	29.68	29.66	29.99	33.00	30.91	29.49	28.89	30.70

Y

33.17	26.95	31.90	29.99	29.50	27.09	28.96	29.46	29.30	29.19
30.95	28.98	28.36	29.63	34.36	28.72	28.60	31.61	27.06	32.12
30.66	29.84	28.83	27.88	31.38	30.71	30.30	28.20	28.74	27.95
32.06	31.26	31.04	28.48	29.88	32.42	27.87	29.85	29.30	31.78

Модуль №5. Основы корреляционного и регрессионного анализа

Индивидуальные задания к модулю № 5

Задание к лабораторной работе 4

В работе приведены результаты наблюдений за парой признаков ( Х,У ). По данным наблюдений требуется:

а) построить корреляционное поле;

б) найти коэффициент корреляции между признаками Х и У;

в) найти уравнение линейной регрессии у = f(x) и дать объяснение полученному результату, используя экономический смысл данных;

г) нанести график прямой регрессии на корреляционное поле и сделать предварительный прогноз.

Вариант 10 (Х - энерговооруженность (относ. ед.); У - производительность труда (относ. ед.))

Х	248	58	186	77	171	88	151	113	138	125
У	30	10	26	14	25	16	22	18	21	20
Х	40	194	68	175	85	154	106	148	121	133
У	6	28	13	25	15	23	18	22	19	21
Х	237	59	180	82	158	91	151	114	136	126
У	30	11	26	15	25	17	22	18	21	20
Х	41	188	70	175	85	152	110	144	122	128
У	9	28	13	25	16	22	18	22	19	20
Х	205	62	178	84	157	94	151	115	135	128
У	29	11	26	15	24	17	22	19	21	21