Определение 10.1. Математическим ожиданием (средним значением) случайной величины называют действительное число, определенное в зависимости от типа случайной величины x формулой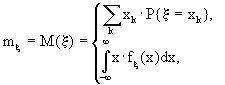

 

если x - дискретна;

если x - абсолютно непрерывна, если ряд (соответственно интеграл) в правой части формулы (10.1) сходится абсолютно.

Теорема 10.1. (Основные свойства математического ожидания)

2. Если с - постоянная, то М(x с) = сМ(x ).

3. Для любых величин x ч Мx ч Ј Мч x ч .

4. Для любых случайных величин x , h

М(x ± h ) = Мx ± Мh , если Мx и Мh существуют.

Пусть x = x (w ) и h = h (w ) определены на вероятностном пространстве

{W, Б , Р}. Сумма x + h является случайной величиной, определенной на том же вероятностном пространстве.

Пусть x задана рядом распределения

, (10.2)

а h - рядом распределения

. (10.3)

Тогда случайная величина x + h принимает значения x_i + y_k, i =1,2, ... k = 1,2, ... ,

.

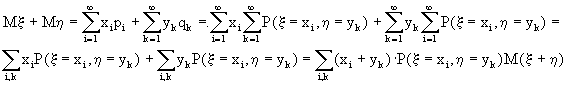
Заметим, что все вышеприведенные преобразования законны, т.к. ряды для Мx и Мh сходятся абсолютно и сними можно обращаться, как с конечными суммами. u

{x = x_i} и {h = у_k }- независимы, то есть

Произвольные случайные величины z ,n независимы, если для любых вещественных х, у события {z < x}, {n <y} независимы, то есть

Теорема 10.2. Если случайные величины x и h независимы, то

М(x h ) = М(x ) М(h )

Д о к а з а т е л ь с т в о. Пусть x и h независимы, с рядами распределения (10.2) и (10.3) . Случайная величина x ^. h дискретна, принимает значения х_i ^.y_k с вероятностями :

Здесь перестановка членов возможна в силу абсолютной сходимости рядов. Ё

Определение 10.3. Дисперсией случайной величины называют неотрицательное число, определенное в зависимости от типа случайной величины x формулой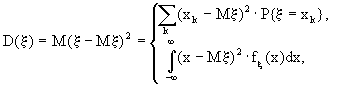

если x - дискретна, (10.4)

если x - абсолютно непр.,

Неотрицательное число называют среднеквадратичным отклонением случайной величины x . Оно имеет размерность случайной величины x и определяет некоторый стандартный среднеквадратичный

интервал рассеивания, симметричный относительно Мx .

Dx = M(x - Mx )² = M[x ² - 2x Mx + (Mx )²] = Mx ² - 2Mx Mx + (Mx )²] = Mx ² - (Mx )².

Отсюда следует, что

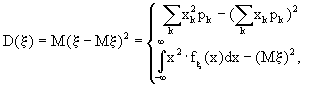
если x - дискретна, (10.4/ )

если x - абсолютно непр.

Теорема 10.3. (Свойства дисперсии)

1. Для любой случайной величины x верно Dx і 0,

2. Если c - постоянная, то Dc = 0.

3. Если c - постоянная, то D(cx ) = c²Dx .

4. Если случайные величины x и h независимы, то

D(x ± h ) = Dx + Dh .

Докажем свойство 4. Воспользуемся определением (10.4/ ), откуда следует

D(x + h ) = M[(x + h ) - M (x + h )]² = M[(x - Mx ) +(h - Mh )]² =

= M(x - Mx )² +M(h - Mh )² + 2 М(x - Mx ) (h - Mh ),

но т.к. случайные величины x и h независимы, то (x - Mx ) и (h - Mh ) тоже независимы, тогда М(x - Mx ) (h - Mh ) = М(x - Mx ) М(h - Mh ) = 0.

Теперь получаем D(x + h ) = M(x - Mx )² +M(h - Mh )² = Dx + Dh . Ё

),

• Случайная величина называется стандартизированной (нормированной), если Mx = 0 и s x = 1.

В оглавление