§ 12. Последовательность независимых испытаний и биномиальный закон распределения

Назовем испытанием любое осуществление случайного эксперимента, производимого последовательно в неизменных условиях. При этом пространство элементарных исходов W при каждом испытании будет одним и тем же. Испытания будем называть независимыми, если верно равенство

,

где Аi - исход i-го испытания, i = 1, 2, ..., n.

Представим себе, что в каждом испытании мы наблюдаем за осуществлением (или неосуществлением) одного и того же события А, вероятность которого, в силу идентичности случайных экспериментов, не зависит от номера испытания, Р(Аi) = p, 0 Ј p Ј 1.

Для краткости речи назовем осуществление события А “успехом”, а осуществление события (неосуществление события А) “неудачей”. Очевидно, , независимо от номера испытания. Последовательность испытаний, в каждом из которых вероятность “успеха” равна р, называют “схемой Бернулли” по имени швейцарского математика Я. Бернулли.

С последовательностью n испытаний Бернулли свяжем случайную величину x n, равную числу “успехов”, наступивших в результате их осуществления. Очевидно, x n принимает одно из значений 0,1, ..., n.

Теорема 12.1. В схеме Бернулли

, (12.1)

где n - число испытаний, p- вероятность “успеха”,

q = 1 - p - вероятность “неудачи”, k = 0, 1, 2, ..., n.

Д о к а з а т е л ь с т в о.

Идею доказательства продемонстрируем вначале на случае, когда n = 2. Возможные исходы двух испытаний можно представить в виде четырех пар символов У и Н: УУ, УН, НУ, НН. В силу независимости испытаний имеем

P(x 2 = 2) = Р(УУ) = p2 ;

P(x 2 = 1) = Р(УН И НУ) = Р(УН) + Р(НУ) = 2pЧ q;

P(x 2 = 0) = Р(НН) = q2.

В общем случае результат n последовательных испытаний, среди которых получено k “успехов” и n - k “неудач”, можно записать в виде строки

(УНУНУУУ ...), в которой всего n символов, из них k литер У, n-k литер Н.

Вероятность каждого такого набора равна (при этом используется независимость испытаний). Количество таких строк (наборов) равно числу способов выбора k различных элементов (мест для литеры У) среди n различных элементов (всех мест строки), то есть .

По теореме сложения вероятность события (x n = k) равна сумме вероятностей всех строк (наборов) указанного выше вида, а поскольку число их и каждая имеет вероятность , то

. Ё

Заметим, что .

Набор вероятностей (k = 0, 1, ..., n) называют распределением Бернулли или биномиальным распределением, а формулу (12.1) - формулой Бернулли.

Теперь, естественно, возникает вопрос о нахождении наиболее вероятного числа успехов. Число , при котором вероятность максимальна, иногда называют наивероятнейшим числом “успехов”.

Теорема 12.2. Если - целое число, то , если - целое число, то имеет два значения и , и, если - не целое число, то заключено в пределах .

Д о к а з а т е л ь с т в о.

Рассмотрим отношение

 

.

Поэтому, если , то ( с ростом k вероятности возрастают) ; если , то ( с ростом k вероятности убывают ). Пусть - наибольшее целое число, не превосходящее. Тогда . Если - целое , то наиболее вероятных значений k0 два Ё

Пример 12.1. Случайная величина x распределена по биномиальному закону. Найти Mx и Dx .

Р е ш е н и е. Запишем ряд распределения случайной величины x .

xi

0

1

2

...

n

Pi

P0(0)

P1(1)

P2(2)

...

Pn(n)

Здесь , k = 0,1,... ,n.

Так как x - дискретная случайная величина, то в силу ( 10.1 )

.

Вынесем за знак суммы общий множитель np, в результате чего получим

.

Сделаем в последней сумме замену i - 1 = k, что даст

,

поскольку p + q = 1.

Итак, , то есть среднее число “успехов” в n независимых испытаниях Бернулли равно произведению числа испытаний на вероятность “успеха” в каждом из них.

Для определения Dx воспользуемся (10.2)

Вычислим :

 

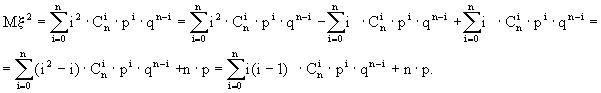
Запишем в последней сумме выражение для :

Вынесем здесь за знак суммы общий множитель :

Сделаем замену i - 2 = k:

Теперь получаем

.

. u

В оглавление