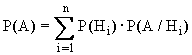Ф_ПВ_Б

§ 6. Формула полной вероятности и формула Байеса

Определение 6.1. Последовательность событий Н₁, Н₂, Н₃, ..., Н_n образует полную группу попарно несовместных событий, если выполнены следующие условия:

1) ,

2) Н_iЗ Н_j = Ж, если i № j, i,j = 1,2,3, ..., n.

Теорема 6.1. Если H₁, ..., H_i, ..., H_n - полная группа попарно несовместных событий и Р( Hi )>0, ( i=1, ..., n ), то для любого события АОБ , имеет место равенство (формула полной вероятности):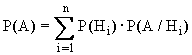

. (6.1)

Д о к а з а т е л ь с т в о.

Событие А, используя равенство А З ( В И С) = (А З В) И (АЗ С), можно записать в виде

А = АЗW = АЗ() = .

Поскольку события Н₁, Н₂, Н₃, ..., Н_n попарно несовместны, то такими же будут и события АЗН₁, АЗН₂, АЗН₃, ..., АЗН_n . В силу аксиомы имеем равенство

Р( А ) = Р{} = .

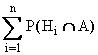Теперь применим теорему умножения к каждому слагаемому последней суммы:

Р( А ) = .= .Ё

З а м е ч а н и е. Формула (6.1) справедлива для счетного набора событий, удовлетворяющих условиям 1),2) из определения 6.1.

Пример 3.6. Три завода поставляют в магазин электролампы. Первый поставляет 45%, второй - 40% и третий - 15% общего количества продаваемых ламп. Продукция первого завода содержит 10% брака, второго - 12% и третьего - 5% брака. Какова вероятность купить в магазине годную лампу?

Р е ш е н и е.

Пусть А - событие “лампа, купленная в магазине, годна к употреблению”, Н_i - событие “ лампа изготовлена на i^м заводе” ( i = 1,2,3).

( Hi иногда называют гипотезами ).

По условию задачи имеем:

Р(H₁) = 45/100 = 0.45; Р(H₂) = 40/100 = 0.40; Р(H₃) = 15/100 = 0.15;

Р( А/H1 ) = 1 - 10/100 = 0.9; Р( А/H2 ) = 1 - 12/100 = 0.88;

Р( А/H3 ) = 1 - 5/100 = 0.95.

Поскольку гипотезы образуют полную группу попарно несовместных событий, то Р(H₁) + Р(H₂) + Р(H₃) = 1.

Используя формулу полной вероятности, получаем

Р( А ) = Р(H₁)Ч Р(А/H1) + Р(H₂)Ч Р(А/H2) + Р(H₃) Р(А/H3) =

= 0.45 x 0.9 + 0.4 x 0.88 + 0.15 x 0.95 = 0.8995. u

Теорема 6.2. ( Формулы Байеса). Пусть набор Hi О Б образуют полную группу попарно несовместных событий, причем Р( Hi )>0 для каждого ( i = 1, ..., n ). Тогда для каждого случайного события, такого что Р( А ) > 0, выполнены равенства:

(6.2)

Д о к а з а т е л ь с т в о.

Воспользуемся теоремой умножения 4.1 по формуле (4.2) имеем

Р( Hi З А ) = Р( Hi ) . Р( А/Hi ) = Р( А) . Р( Hi/А ) , откуда

получаем

где 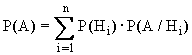(формула полной вероятности).

Для завершения доказательства остается заменить знаменатель в предыдущей формуле.Ё

З а м е ч а н и е. Рассмотрим общую схему применения формул Байеса при решении практических задач. Пусть событие А О Б может происходить в различных условиях, о характере которых можно сделать n гипотез H₁, ..., H_i, ..., H_n . Из каких-то соображений известны вероятности этих гипотез Р(Hi ) - ( априорные вероятности ). Предположим, что произведен опыт, в результате которого наступило событие А. Это должно вызвать переоценку вероятностей гипотез Hi , (i=1ё n ); формулы Байеса и дают выражение для условных вероятностей Р( Hi / А ) - ( апостериорные вероятности ).

Пример 3.6. Пусть в урне пять шаров; предположения о количестве белых шаров равновозможные. Из урны наудачу взят шар, он оказался белым. Какое предположение о начальном составе урны наиболее вероятно?

Р е ш е н и е.

Пусть Hi - гипотеза, состоящая в том, что в урне i белых шаров ( i = 0,1, ...,5), т.е. возможно сделать шесть предположений. Тогда по условию задачи имеем Р(H₀) = Р(H₁) = ... = Р(H₅) = 1/6.

Введем событие А - { наудачу взятый шар белый }. Вычислим Р(Hi /А). Так как Р(А/Hi ) = i/5, то по формуле (6.2) имеем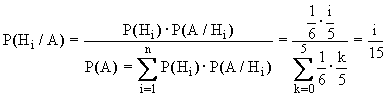

Таким образом, наиболее вероятной является гипотеза H₅

т.к. Р(H₅/А) = 1/3.u

В оглавление