§ 13. Предельные теоремы в схеме Бернулли

В приложениях часто приходится выяснять вероятности различных событий, связанных с числом успехов в n испытаниях Бернулли при больших значениях n . В этом случае вычисления по формуле (12.1) становятся затруднительными. Трудности возрастают, когда приходится еще суммировать вероятности (12.1).

(13.1)

Затруднения возникают также при малых значениях p и q . Иногда при больших значениях n удается заменить формулу (12.1) какой-либо приближенной асимптотической формулой. Приведем три предельные теоремы, содержащие асимптотические формулы для (12.1) и (13.1) при .

Теорема 13.1. ( Теорема Пуассона ).

Если и так, что

то

, (13.2)

при любом m = 0, 1, 2, ... .

Д о к а з а т е л ь с т в о.

Пусть , представим вероятность Р{x n = m} в виде

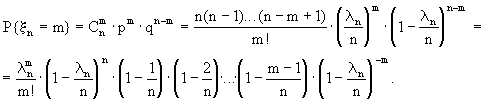
Если теперь , то получим утверждение теоремы. n

Таким образом, при больших n и малых р мы можем воспользоваться приближенной формулой

(13.2.1)

В случае, когда оба параметра p, q заметно отличны от нуля (порядок 0.5) на практике используются следствия из теорем Муавра-Лапласа (локальной и интегральной), которые приведем здесь без доказательства.

Теорема 13.2. (Локальная теорема Муавра-Лапласа). Если , а р (0<p<1) - постоянно, величина равномерно ограничена по n и m , то

, (13.3)

где , при ,

c- постоянная.

Отметим, что значения функции табулированы. Это упрощает использование ее на практике.

При качественной оценке условий применимости приближенной формулы

(13.3.1)

нужно оценить величину остаточных членов в (13.3). Хорошие приближения эта формула дает при p=q=1/2, ее часто используют при n>100 и npq>20. Указания о границах применимости формул (13.2.1) и (13.3.1) являются приближенными, к ним следует относится с осторожностью.

 

Теорема 13.3. (Интегральная теорема Муавра-Лапласа).

Если р (0<p<1) постоянно, то при

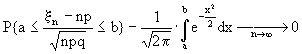
равномерно по a,b, .

Приближенная формул

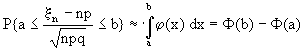(13.4)

используется в тех случаях, когда возможно использование (13.3.1). Отметим, что (13.4) эквивалентна другой формуле

, (13.4.1)

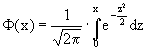где ; , а - функция, называется

функцией Лапласа. Она имеет следующие свойства:

1. Ф(0) = 0;

2. ;

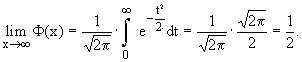3. Ф(-х) = Ф(х), (х > 0).

Значения функции Ф(х) табулированы (см. приложение № 2).

Пример 13.1. Пусть вероятность выпуска сверла повышенной хрупкости равна 0,02. Сверла укладываются в коробки по 100 штук. Чему равна вероятность того, что в коробке не окажется бракованных сверл ?

Р е ш е н и е.

Мы находимся в условиях применимости схемы Бернулли со следующими параметрами: p = 0,02 ; n = 100 ; m = 0 ; q = 1 - p = 0,98; np = 2.

Сравним точные и приближенные значения искомой вероятности.

По формуле Бернулли:

.

По формуле Пуассона:

.

Формула Лапласа дает:

.

Легко видеть, что погрешность, даваемая формулой Лапласа, довольно велика. Если же число испытаний растет, то разница между значениями, даваемыми формулами Пуассона и Лапласа тем меньше, чем больше n . u

Рассмотрим одно важное следствие, которое можно получить из (13.4).

Следствие 13.3.1. Формула (13.4) позволяет оценить близость частоты и вероятности. Пусть p - вероятность успеха в схеме Бернулли и - общее число успехов. Частотой успеха называют отношение . Оценим вероятность события . Если n достаточно велико, тогда, используя (13.4) получим:

(13.5)

Часто возникает обратная задача: сколько нужно провести испытаний, чтобы частота отличалась от вероятности p не больше, чем на e > 0 с

некоторой вероятностью 1 - a (a - мало ) .

В оглавление