§
11. Начальные и центральные моментыОпределение 11.1.
Начальным моментом k-го порядка (k=1, 2, ...) распределения случайной величины x (если он существует) называют действительное число a k = a k (x ), равное математическому ожиданию случайной величины x k, определенное по формуле
если
x - дискретна, (11.1)если
x - абсолютно непрерывна.Определение 11.2.
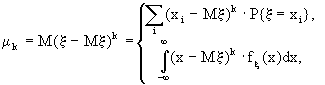
если
x - дискретна, (11.2)если
x - абсолютно непрерывна.З а м е ч а н и я
:n
Число МЅ x Ѕ k называется абсолютным начальным моментом порядка k;n
Число МЅ x - Мx Ѕ k называется абсолютным центральным моментом порядка k случайной величины x ;а)
a 0 = m 0 = 1 ;б)
M x = a 1 ;в) D
x = s 2 x = m 2 = a 2 - a 1 2 ;г)
m 1 = 0.