§ 5. Независимые случайные события

Введем понятие независимости случайных событий, которое в теории вероятностей играет важную роль.

Определение 5.1. Пусть ( W, Б , Р) - вероятностное пространство.

События А, В О Б называются независимыми, если

Р(АЗВ) = Р(А) Ч Р(В). (5.1)

Для независимых событий вероятность совместного появления двух событий равна произведению их вероятностей.

Докажем некоторые простые свойства вероятностей для независимых событий.

Теорема 5.1. Пусть Р(В) > 0. Случайные события А и В независимы тогда и только тогда, когда Р( А/В ) = Р( А )

(появление события В не изменяет вероятности события А).

Д о к а з а т е л ь с т в о.

Пусть А, В независимы и Р( В ) > 0, тогда

Р( А/В ) = = Р( А ).

Обратно, пусть выполнено условие Р(А/В) = Р(А). Тогда

= Р(А/В) = Р(А), а это значит, что Р(АЗВ) = Р(А) Р(В)

и согласно определению 5.1 события А, В независимы. Ё

Независимость событий взаимна, т.е. если событие А не зависит от В, то и событие В не зависит от А.

Пример 5.1. Рассмотрим события А и В из примера 2.2. Опыт состоит в подбрасывании игральной кости:

W={ w1, w2 , w3, w4, w5, w6 }, А = { w2 , w4, w6 }, В = { w3, w6 }.

Используя классическое определение, получим:

Р( В ) = 2/6 = 1/3;

Р( В/А ) =1/3, и по теореме 5.1 А, В - независимые события. u

Упражнение. Доказать, что если А, В независимы, то событие А и ; и также независимы (Самостоятельно).

Определение 5.2. Случайные события А1, А2, А3, ... , Аn независимы в совокупности, если для любого к ( к = 1, ..., n ) и для любого набора индексов i1,i2, ..., ik: ( ik = 1, ..., n )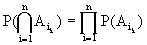

.

З а м е ч а н и е. Если Аi, ( i = 1, ..., n ) независимы в совокупности, то любые два события Аi и Аj ( i № j ) независимы. Однако из по парной независимости не следует независимости в совокупности.

Пример 5.2. (С.Н. Бернштейна).

На плоскость бросают тетраэдр, три грани которого окрашены соответственно в красный, зеленый, голубой цвета, а на четвертую грань нанесены все три цвета.

В оглавление

Рассмотрим вероятности следующих событий:

К - (выпадет грань с красным цветом);

З - (выпадет грань с зеленым цветом);

Г - (выпадет грань с голубым цветом).

Очевидно, что

Р( К ) = Р( З ) = Р( Г ) = 2/4 = 1/2;

Р( КЗЗ ) = Р( КЗГ ) = Р( ГЗЗ ) = P(Г ) Р(З) = 1/4;

Р( КЗЗЗГ ) = 1/4 № Р( К ) Р( З ) Р( Г ) = 1/8.

В оглавление