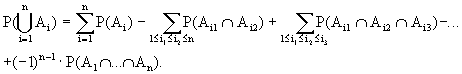§ 3. Основные теоремы теории вероятностей

(Свойства вероятностей)

Исходя из аксиом (Р1, Р2, Р3) установим ряд важнейших свойств вероятностей случайных событий.

Теорема 3.1. Вероятность события , противоположного событию А, равна:

Р() = 1 - Р(А). (3.1)

Д о к а з а т е л ь с т в о.

Т.к. А И = W,

А З = Ж, то согласно , , имеем:

Р( А И ) = Р(А) + Р() = Р(W) = 1, откуда Р( ) = 1 - Р(А). Ё

Следствие 3.1. Вероятность невозможного события равна нулю Р( Ж ) = 0

Д о к а з а т е л ь с т в о.

Положим в равенстве (3.1), которое справедливо для каждого случайного события А О Б , А = W . Тогда Р(Ж) = Р() = 1 - Р(W) = 0.

 

З а м е ч а н и е. Вероятность невозможного события равна нулю, но событие нулевой вероятности не обязательно есть невозможное событие.

 

Теорема 3.2. Пусть А и В случайные события, такие, что А М В и

А, В О Б . Тогда

Р( В \ А ) = Р( В ) - Р( А ). (3.2)

 

Д о к з а т е л ь с т в о.

 

Так как А М В , то В = А И ( В \ А ) , причем А З ( В \ А ) = Ж.

Поэтому по аксиоме Р( В ) = Р( А ) + Р( В \ А ), откуда получаем

Р( В \ А ) = Р( В ) - Р( А ). Ё

Следствие 3.2. Если А М В, то Р( А ) Ј Р( В ).

Д о к а з а т е л ь с т в о следует из А1, т.к. Р( В \ А ) і 0, то из равенства 3.2 имеем

Р( В ) - Р( А ) і 0, откуда Р( В ) і Р( А ).

 

Следствие 3.3. Для каждого случайного события А О Б , 0 Ј Р(А) Ј 1.

В самом деле, А М W, поэтому Р( А ) Ј Р( W ) = 1.

 

Теорема 3.3. (Теорема сложения вероятностей).

Пусть А и В случайные события А, В О Б . Тогда

Р( В И А ) = Р( В ) + Р( А ) - Р( А З В ). (3.3)

 

Д о к а з а т е л ь с т в о.

 

Представим А И В в виде объединения трех попарно непересекающихся событий

АИВ = { А \ (АЗВ)} И { В \ (АЗВ)} И (АЗВ).

По аксиоме и теореме 3.2 получим

Р( АИВ ) = Р{{ А \ (АЗВ)} И { В \ (АЗВ)} И (АЗВ)} =

= Р{А \ (АЗВ)} + Р{ В \ (АЗВ)} + Р(АЗВ) =

= Р( А ) - Р( АЗВ ) + Р( В ) - Р(АЗВ) + Р(АЗВ) =

= Р( А ) + Р( В ) - Р(АЗВ). Ё

 

Следствие 3.4. Из теоремы 3.3 легко получить формулу для вероятности суммы любого конечного числа событий.

Путь А1, А2, А3, ... , Аn О Б - случайные события. Тогда

В оглавление