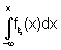 , (9.1)
, (9.1)§
9. Непрерывные случайные величиныПусть
{ W , Б , Р } - вероятностное пространство. Случайная величина x (w ) называется абсолютно непрерывной случайной величиной, если существует неотрицательная функция fx (х) такая, что при любом хО R Fx(х) = Р{w :x(w ) < х} =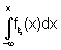 , (9.1)
, (9.1)
f
x (х) называется плотностью распределения вероятностей абсолютно непрерывной случайной величины x .Плотность распределения вероятностей обладает следующими свойствами:
2.  = 1 - условие нормировки;
= 1 - условие нормировки;
3. ![]() - в точках непрерывности fx (х);
- в точках непрерывности fx (х);
4. P( a Ј x < b) =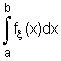 = Fx (b) - Fx (a) , для любых a < b; a,b О R.
= Fx (b) - Fx (a) , для любых a < b; a,b О R.
З а м е ч а н и е
. Функция распределения непрерывной случайной величины x является непрерывно монотонно неубывающей функцией на всей числовой оси. Причемзначит, вероятность того, что
x примет данное конкретное значение х, равна нулю.Пример 9.1. Дана функция
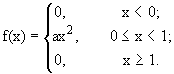
а) При каком значении
а функция f(x) является плотностью распре- деления случайной величины x ?б) Выписать F
x (x) и построить графики Fx (x) и fx (х).в) Найти вероятность того, что случайная величина примет значение в интервале (-1;
1/2).Р е ш е н и е.
а) Используя условие нормировки (2), имеем:
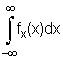 =
=![]() + а
+ а![]() +
+![]() =
=![]() =1, отсюда а = 3.
=1, отсюда а = 3.
Итак, при а = 3 функция f(x) является плотностью распределения неко-торой случайной величины
x :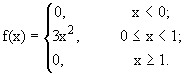
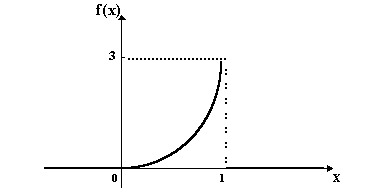
Ее график имеет вид:
Рис. 9.1
б) Определим F
x (x), используя (9.1)
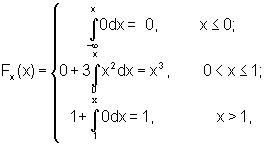
график функции распределения F
x (x) имеет вид: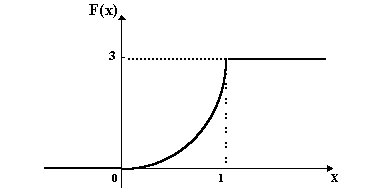
Рис. 9.2
в) Найдем
P( -1 < x < 1/2) =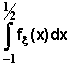 = Fx (1/2) - Fx (-1) = 1/8,
= Fx (1/2) - Fx (-1) = 1/8,
действительно,
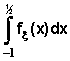 =
=![]() + 3
+ 3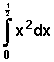 =
=![]() =1/8. u
=1/8. u