Р{ w: x(w) = хi}, (8.2)§
8. Дискретные случайные величиныПусть {
W, Б , Р } - вероятностное пространство. Случайная величина x(w) называется дискретной, если она принимает конечное или счетное число значений.Если х
1 , х2 , ... , хn , ... - значения дискретной случайной величины, то для каждого n {w: x(w) = хn} О Б , и можно определить вероятностьрn = Р{ w: x(w) = хn}. (8.1)
Набор вероятностей р
n (8.1) называется распределением дискретной случайной величины x(w). Дискретную случайную величину x(w) удобно характеризовать с помощью табл. 8.1.Таблица 8.1
|
xi |
х 1 |
х 2 |
... |
х n |
... |
|
pi |
р 1 |
р 2 |
... |
р n |
... |
Заметим, что рi
і 0,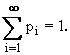
Таблица (8.1) называется рядом распределения дискретной случайной величины.
Графическое изображение ряда распределения дискретной случайной величины наглядно характеризует многоугольник распределения случайной величины. Многоугольник случайной величины строится следующим образом: по оси абсцисс отложить х1, х2,..., хn , а по оси ординат р1 ,р2, ..., рn и соединить соседние точки с координатами (хi, pi) на плоскости отрезками.
Зная закон (ряд) распределения дискретной случайной величины, можно построить функцию распределения, представляющую собой в этом случае функцию накопленных вероятностей
Fx(х) = Р{ w: x(w) = хi}, (8.2)
где суммирование распространяется на все значения индекса i, для которых х
i< х. Из (8.2) следует, чтоFx(хк+0) - Fx(хк) =Р{ x = хк},
хк
О{ х1 , х2 , ... , хn , ... }, т.е. функция распределения испытывает скачки в точках хк, для которых Р{x = хк} > 0.Пример 8.1.
Игрок трижды бросает симметричную монету. Он получает $1 при каждом появлении "герба", и платит $1 при каждом появлении "решетки".Обозначим x его “выигрыш” после третьего бросания.
Найти:
б) функцию распределения x. Построить график функции распределения.
Р е ш е н и е.
а). Пространство элементарных событий состоит из восьми элементов
W
= { w1 = (РРР), w2 = (РРГ), w3 = (РГР), w4 = (ГРР), w5 = (ГГР), w6 = (ГРГ), w7 = (РГГ), w8 = (ГГГ) }.Вычисляем значения
x:x( w1 ) = -3, x( w2 ) = x( w3 ) = x( w4 ) = -1,
x
( w5 ) = x( w6 ) = x( w7 ) = 1, x( w8 ) = 3.Теперь вычислим соответствующие вероятности:
Р{
x = -3} = 1/8, P{x = -1} = 3/8, P{x = 1} = 3/8, P{x = 3} = 1/8.Ряд распределения имеет вид:
|
хi |
-3 |
-1 |
1 |
3 |
|
р i |
1 /8 |
3 /8 |
3 /8 |
1 /8 |
Построим многоугольник распределения для случайной величины
x .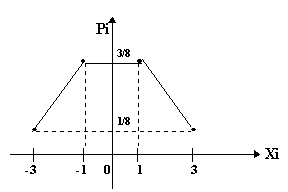
Теперь можно записать аналитический вид функции распределения F
x(х): если х Ј -3, то событие { w: x(w) < х} является невозможным иР{
w: x(w) < х} = 0.Если -3 < x
Ј -1, то Р{ w: x(w) < х} = 1/8, и т.д. Согласно (8.2) будем иметь: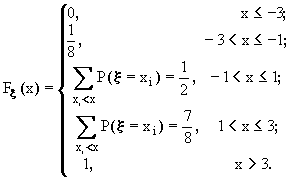
График функции распределения имеет вид:
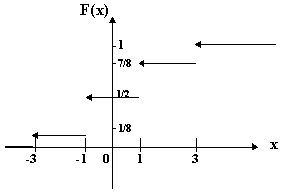
Рис. 8.1