§
4. Условные вероятностиВ ряде случаев приходится рассматривать вероятности случайных событий, если известно, что произошло некоторое другое случайное событие, имеющее положительную вероятность.
Сначала рассмотрим несколько примеров.
Пример 4.1. Рассмотрим следующий случайный эксперимент.
Из урны, в которой находится вначале 6 белых и 4 черных шара, наудачу извлекается последовательно два шара, причем вынутый шар обратно не возвращается. Предполагаем, что все шары различны (шары отличаются только цветом).
Обозначим А,В события “ первый вынутый шар будет белый”, “второй вынутый шар будет белый”.
Вычислим вероятности Р(А), Р(В), Р(А
З В) и P(A/B) - “условную” вероятность того, что первый шар белый, если известно, что белым оказался второй шар.В данной задаче пространство
W состоит из 10Ч 9 = 90 элементов, из которых 6Ч 9 = 54 элементарных исхода благоприятствуют событию А,6Ч 5 + 4Ч 6 = 54 благоприятствуют событию В, 6Ч 5 = 30 благоприятствуют событию
А З В. Пользуясь классическим определением вероятности события, получаем:
Р( В ) = Р( А ) = mА/n = 54/90 =6/10 = 3/5 ,
Р(А
З В) = 30/90 =1/3.Если известно, что событие В произошло, то вместо 90 возможных элементарных исходов, может произойти лишь один из 6
Ч 5 + 4Ч 6 = 54 исходов, из которых 6Ч 5 = 30 благоприятствуют событию А . ПоэтомуP(A/B) = ![]() .
.
Как видим, дополнительная информация (событие В произошло) об исходе эксперимента изменила вероятность события А.
![]() .
.
Заметим ещё следующее обстоятельство, использованное при подсчете “условной” вероятности
P(A/B) = ![]() .
.
Оказывается, последнее равенство допускает обобщение.
uПример 4.2.
Путь пространство элементарных исходов состоит из n одинаково возможных событий, событию А благоприятствуют mА элементарных исходов, В - ml исходов и событию А З В - mr исходов. Найдем Р( А/В ).
Заметим, что ![]()
Если событие В произошло, то произошло одно из m
l элементарных событий, и тогда событие А произойдет, когда произойдет одно из mr элементарных событий, благоприятствующих событию А З В. ПоэтомуP( А/В ) = 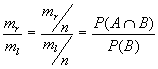
Определение 4.1.
Пусть ( W, Б , Р) - вероятностное пространство,Р( В ) > 0, В
О Б . Условной вероятностью события А О Б при условии, что событие В имело место, называют отношениеР( А/В ) = ![]()
Из определения 4.1 и свойств вероятности следуют свойства условной вероятности:
1) Р( А/В )
і 0;2) Р(
W/В ) = 1;3) Р( В/В ) = 1;
4) Если Аi (i =1,2, ...) - последовательность попарно несовместных
событий Аi
З Аj = Ж, ( i № j ), тоУпражнение: доказать самостоятельно 2), 4).
Теорема 4.1.
( Теорема умножения). Если Р( В ) > 0, Р( А ) > 0, то имеет место равенстваР(АЗВ) = Р(А)Ч Р(В/А) = Р(В) Р(А/В). (4.2)
(Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое имело место.)
Д о к а з а т е л ь с т в о.
Доказательство следует из равенства (4.1) и допускает следующее обобщение, которое доказывается методом математической индукции.
Р(![]() ) = Р( А
) = Р( А
где Аi (i =1,2, ...) - случайные события такие, что Р(А
1З...ЗАк ) > 0, к=1, ..., n. Ё