Рассмотрим некоторые наиболее важные законы распределения случайных величин.
![]() 2. Экспоненциальное (показательное) распределение
2. Экспоненциальное (показательное) распределение
![]()
Непрерывная случайная величина
x имеет равномерное распределение на отрезке [a,b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю, т.е.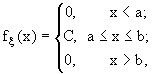
где С = Const. Используя условие нормировки 2 из
§ 9, определим С.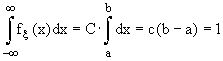 ,
,
откуда с = 1/(b-a) и, следовательно, плотность равномерного распределения имеет вид:
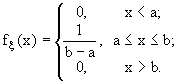 (14.1)
(14.1)
Теперь определим вид интегральной функции распределения для этого закона, который в силу (9.1) будет следующим:
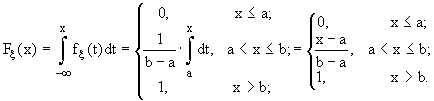 (14.2)
(14.2)
Изобразим графики f(x) и F(x):
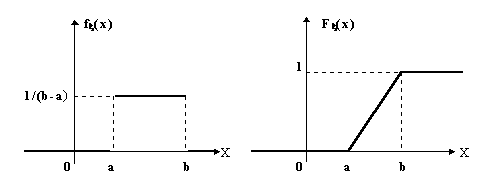
Рис. 14.1
Определим числовые характеристики данной случайной величины:
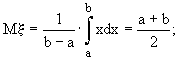 (14.3)
(14.3)
 (14.4)
(14.4)
![]() (14.5)
(14.5)
Наконец, найдем вероятность попадания значений равномерно распределенной случайной величины на интервале (a,b) в интервал (
a , b ): 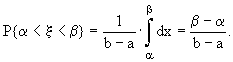 (14.6)
(14.6)
Непрерывная случайная величина подчинена равномерному закону распределения, если ее возможные значения лежат в пределах некоторого определенного интервала, кроме того, в пределах этого интервала все значения случайной величины одинаково вероятны (обладают одной и той же плотностью вероятности). С такими случайными величинами часто встречаются в измерительной практике при округлении от счетов измерительных приборов до целых делений шкал. Ошибка при округлении отсчета до ближайшего целого деления является случайной величиной
x , которая с постоянной плотностью вероятности принимает любое значение между соседними целыми делениями.![]()
Исключительно важную роль в теории вероятностей играет нормальное распределение (закон Гаусса).
Непрерывная случайная величина
x имеет нормальное распределение вероятностей с параметрами а, s > 0, если плотность распределения ее имеет вид: 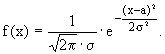
Нормальный закон распределения широко применяется в практических задачах, он проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. Каждый фактор в отдельности на величину
x влияет незначительно.Функция распределения такой случайной величины имеет вид:
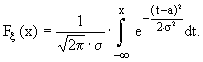 (14.13)
(14.13)
Для определения числовых характеристик воспользуемся интегралом Пуассона:
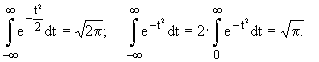 (14.14)
(14.14)
Имеем:
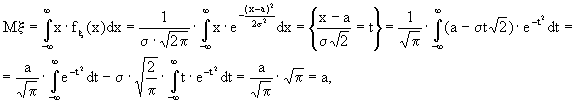
то есть M
x = a. (14.15)Далее,
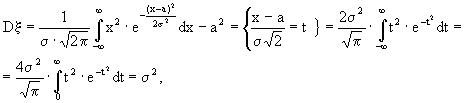
итак:
D
x = s 2 . (14.16)Таким образом, параметры а,
s 2 в выражении (14.12) есть математическое ожидание и дисперсия нормально распределенной случайной величины, а ![]() (14.17)
(14.17)
График плотности вероятности имеет вид нормальной кривой (Гаусса):
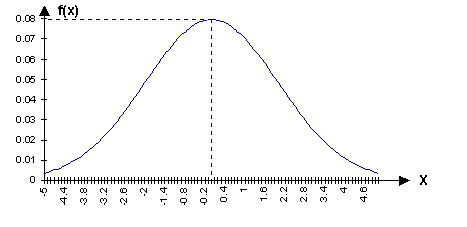
Рис. 14.3
Отметим некоторые свойства нормальной кривой.
1. Кривая распределения симметрична относительно прямой х = а.
2. ![]()
3. ![]()
4. При изменении математического ожидания и при
s = Const, происходит смещение кривой вдоль оси Ох. Если положить а = Const и изменять s , то кривая изменяет свой вид в зависимости от s .
Рис. 14.4
Замечание. Пусть
x - нормальная случайная величина с параметрами (0,1), Тогда ее плотность имеет вид:![]() ,
,
а функция распределения
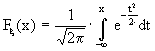 (14.18)
(14.18)
есть функция Лапласа (см. (13.4
\)).С помощью Ф(х) можно вычислять вероятность того, что нормальная случайная величина с параметрами (а,
s 2) примет значение из интервала (a ,b ).Именно,
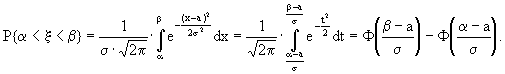 (14.20)
(14.20)
Отметим важный частный случай последней формулы:
![]() (14.21)
(14.21)
Если взять
![]() (14.22)
(14.22)
Формула (14.22) носит название правила трех сигм
.![]()
2. Экспоненциальное (показательное) распределение
данныеВ практических приложениях теории вероятностей, особенно в теории массового обслуживания, исследовании операций, в физике, биологии, теории надежности, часто имеют дело со случайными величинами, которые имеют экспоненциальное распределение.
Случайная величина
x распределена по показательному закону с параметром l >0, если она непрерывна и имеет следующую плотность распределения вероятностей: 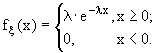 (14.7)
(14.7)
Тогда
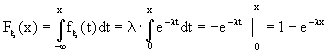 (x > 0).
(x > 0).
Таким образом,
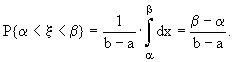 (14.6)
(14.6)
соответственно, графики f(x) и F(x) имеют вид:
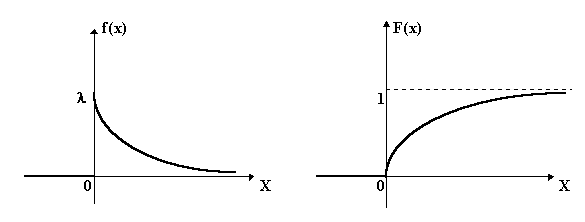 Рис. 14.2
Рис. 14.2
Определим числовые характеристики:
 (14.9)
(14.9)
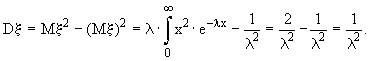 (14.10)
(14.10)
![]() (14.11)
(14.11)