Лемма (Маркова)§
15. Закон больших чиселТеория вероятностей изучает закономерности, свойственные массовым случайным явлениям. Познавательная ценность теории вероятностей обусловлена тем, что массовые случайные явления в своем совокупном действии создают строгие закономерности. Само понятие математической вероятности было бы бесплодно, если бы не находило своего осуществления в виде частоты появления какого либо результата при многократном повторении однородных условий.
При достаточно большом числе испытаний характеристики случайных событий и случайных величин, наблюдаемых при испытании, становятся почти неслучайными.
Группа теорем, устанавливающих соответствие между теоретическими и экспериментальными характеристиками случайных величин и случайных событий при большом числе испытаний над ними, а также касающихся предельных законов распределения, объединяются под общим названием предельных теорем теории вероятностей.
Познакомимся с группой утверждений и теорем, объединенных общим названием закон больших чисел.
Рассмотрение теорем закона больших чисел начнем с леммы Маркова и неравенства Чебышева, с помощью которых значительно упрощаются доказательства теорем закона больших чисел.
Закон больших чисел в форме Чебышева
Закон больших чисел в форме Маркова
Центральная предельная теорема
(15.1)
Д о к а з а т ь е л ь с т в о.
Проведем доказательство для дискретной случайной величины способом, получившим название метода урезания
.Пусть | x
1|, | x2 |, ..., | xn | - есть упорядоченная совокупность всех значений случайной величины x , с соответствующими вероятностнымиpi = P{|
x | = | xi | }, причем е pi = 1.Не нарушая общности доказательства, можно допустить, что абсолютные значения случайной величины
x расположены в порядке убывания. Выберем произвольное e >0 и предположим, что первые r значений совокупности не меньше e (r Ј n) . Запишем следующее неравенство:| x1 | p1 + | x2 | p2 + ... + | xr | pr
Ј | x1 | p1 + ... + | xr | pr + ... + | xn | pn = M | x | .Следовательно,
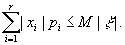
Заменяя в левой части последнего неравенства значение |x
i| числом e , получим усиленное неравенство:e
Ч
pi Ј M | x | или 
.
Левая часть выражает вероятность того, что модуль случайной величины принимает значение, не меньшее
e , т.е. .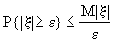
Замечание
.1.
Вероятность противоположного события, а именно вероятность того, что { | x | < e } удовлетворяет следующему неравенству 
. (15.1
2.
3.
Лемма Маркова справедлива для любого закона распределения. В силу того, что величина вероятности не может быть больше единицы и меньше нуля, при использовании неравенства (15.1) и (15.1ў ) следует иметь в виду, что для получения содержательных утверждений e следует выбирать так, чтобы было верно неравенство
.
Лемма 15.2
(Неравенство Чебышева). Если случайная величина имеет конечное математическое ожидание и дисперсию, то для любого положительного числа e справедливо неравенство 
.
Д о к а з а т е л ь с т в о.
Воспользуемся леммой 15.1. Рассмотрим случайную величину
h
= | x - M x | . Т. к. случайная величина h - положительна, то неравенства|
x - M x | < e и (x - M x )2 < e 2 равносильны. Применим лемму Маркова к случайной величине h 2 . Тогда имеем
.
В силу равносильности неравенств 
и 
} = P{}, откуда получаем
. n
Замечание.
1
. Очевидно, что 
. (15.2/)
2
3
. Неравенство Чебышева для практики имеет ограниченное значение, поскольку часто дает грубую оценку. Пусть, например, e = s /2, тогда в силу (15.2’) имеем
.
Но и без того ясно, что вероятность не может быть больше единицы.
Если теперь e = 10s , то
.
Это неплохая оценка вероятности. Однако следует отметить, что теоретическое значение неравенства Чебышева очень велико.
Определение 15.1.
Последовательность случайных величин x 1,x 2, ..., x n называется сходящейся по вероятности при
к случайной величине x 
, если для всех e > 0 
, или, что эквивалентно, 
Закон больших чисел в форме Чебышева
Теорема 15.1
. (Закон больших чисел в форме Чебышева)Пусть случайные величины
x 1, x 2, ..., x n, ... , попарно независимы и имеют конечные дисперсии, ограниченные одной и той же постоянной с: Dx i Ј c, i = 1,2, ... . Тогда для любого e > 0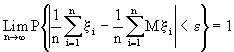 
.
Д о к а з а т е л ь с т в о
.В силу условия теоремы верно 
. Воспользуемся неравенством Чебышева (15.2)
.
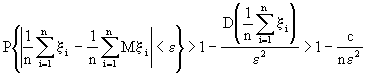Переходя к пределу при в последнем неравенстве, получаем 
, а так как вероятность любого события не превышает единицы, то
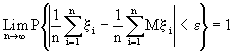. n
Таким образом, закон больших чисел устанавливает условия сходимости среднего арифметического n случайных величин к среднему арифметическому их математических ожиданий.
Закон больших чисел в форме Маркова
Теорема 15.2.
(Закон больших чисел в форме Маркова)Если последовательность произвольных случайных величин
x 1, x 2, ..., x n, удовлетворяет условию 
. (15.3)
Д о к а з а т е л ь с т в о.
Рассмотрим случайную величину
и ее математическое ожидание
,
и дисперсию 
Применив неравенство Чебышева, получим:
или
.
Переходя к пределу в последнем неравенстве при , получаем (15.3).
Теорема 15.3.
(Бернулли). Пусть m n - число наступлений события А в n независимых испытаниях Бернулли, р - вероятность наступления события А в одном испытании. Тогда для любого e >0 
. (15.4)
Д о к а з а т е л ь с т в о
.Из того, что случайная величина
m n распределена по биномиальному закону имеем, М(m n) = np, D(m n) = npq и тогда М(m n/n) = p, а D(m n /n) = pq/n. Неравенство Чебышева принимает следующий вид: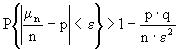
.
Переходя к пределу в последнем неравенстве при , получаем (15.4)
Теоремы закона больших чисел, которые устанавливают факт сходимости по вероятности некоторых случайных величин к постоянным их характеристикам независимо от их закона распределения. Группа теорем, касающихся предельных законов распределения суммы случайных величин, носит общее название центральной предельной теоремы. Центральная предельная теорема в форме А. М. Ляпунова устанавливает условия, при которых указанный предельный закон является нормальным.
Интегральная и локальная теоремы Муавра-Лапласа также являются следствиями центральной предельной теоремой для последовательности независимых одинаково распределенных случайных величин, принимающих два значения (см. теоремы 13.2 и 13.3).
Теорема 16.1.
(Ляпунова). Если случайные величины в последовательности {x n},(n=1,2, ...) независимы, одинаково распределены и имеют конечное математическое ожидание Мx n и дисперсию Dx n , а также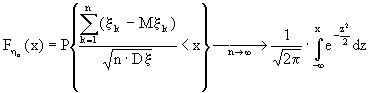
, то для любого действительного х
.
Говорят, что последовательность случайных величин
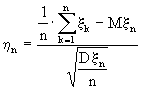, n = 1,2,...
асимптотически нормальна.