Статистические оценки неизвестных параметров  распределения

 

          Как уже говорилось, изучая генеральную совокупность, мы на самом деле изучаем некоторую случайную величину x. Последняя же становится известной, если известно ее распределение (плотность или функция распределения). В типичных задачах вид функции распределения x известен с точностью до некоторых параметров.

          Например:

·           в теории измерений считается, что ошибки измерений подчинены нормальному закону с плотностью

и задача состоит в определении а либо s, либо обоих параметров одновременно.

·           Количество несчастных случаев часто предполагают распределенным по закону Пуассона

и задача состоит в определении параметра l.

·           В теории надежности предполагают, что длительность безотказной работы прибора подчинена показательному закону распределения с параметром m:

и снова возникает задача об определении одного параметра.

          Вся информация, которой мы располагаем при решении указанных задач, содержится в выборке ().

Определение 21.1. Оценкой неизвестного параметра Q называют любую (борелевскую) функцию n переменных от выборки:

          Поскольку оценка является функцией от случайного вектора (выборки), она сама является случайной величиной, распределение которой зависит от числа наблюдений n и оцениваемого параметра Q.

 

Основные свойства точечных оценок

 

          Для того чтобы оценка  имела практическую ценность, она должна обладать следующими свойствами.

·     1. Оценка  параметра q называется несмещенной, если ее математическое ожидание равно оцениваемому параметру  q , т.е.

                                                М = q .                                                  (22.1)

Если равенство (22.1) не выполняется, то оценка  может либо завышать значение q  (М >q ), либо занижать его (М < q ) . Естественно в качестве приближенного неизвестного параметра брать несмещенные оценки для того, чтобы не делать систематической ошибки в сторону завышения или занижения.

·     2. Оценка   параметра q называется состоятельной , если она подчиняется закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру при неограниченном возрастании числа опытов (наблюдений ) и, следовательно, выполняется следующее равенство:

,                                      (22.2)

где e > 0 сколько угодно малое число.

          Для выполнения (22.2) достаточно, чтобы дисперсия оценки стремилась к нулю при , т.е.

                                                          (22.3)

и кроме того, чтобы оценка была несмещенной. От формулы (22.3) легко перейти к (22.2) , если воспользоваться неравенством Чебышева.

          Итак, состоятельность оценки означает, что при достаточно большом количестве опытов и со сколько угодно большой  достоверностью отклонение оценки от истинного значения параметра меньше любой наперед заданной величины. Этим оправдано увеличение объема выборки.

          Так как  - случайная величина, значение которой изменяется от выборки к выборке, то меру ее рассеивания около математического ожидания q будем характеризовать дисперсией D. Пусть  и  - две несмещенные оценки параметра q, т.е. M = q и M = q ,  соответственно D  и D и, если D  < D , то в качестве оценки принимают .

·     3. Несмещенная оценка , которая имеет наименьшую  дисперсию среди всех возможных несмещенных оценок параметра q, вычисленных по выборкам одного и того же объема , называется эффективной оценкой.

           На практике при оценке параметров не всегда удается удовлетворить одновременно требованиям 1, 2, 3. Однако выбору оценки всегда должно предшествовать ее критическое рассмотрение со всех точек зрения. При выборке практических методов обработки опытных данных необходимо руководствоваться сформулированными свойствами оценок.

 

Оценка математического ожидания и дисперсии по выборке

 

          Наиболее важными характеристиками случайной величины являются математическое ожидание и дисперсия. Рассмотрим вопрос о том,  какие выборочные характеристики лучше всего оценивают математическое ожидание и дисперсию в смысле несмещенности, эффективности и состоятельности.

Теорема 23.1.  Арифметическая средняя , вычисленная по n независимым наблюдениям над случайной величиной x, которая имеет математическое ожидание Mx = m, является несмещенной оценкой этого параметра.

 

Д о к а з а т е л ь с т в о.

 

          Пусть - n независимых наблюдений над случайной величиной x. По условию Mx = m, а т.к.  являются случайными величинами и имеют тот же закон распределения, то тогда . По определению средняя арифметическая

                                      .                                     (23.1)

          Рассмотрим математическое ожидание средней арифметической. Используя свойство математического ожидания, имеем:

                      ,

т.е. . В силу (22.1)  является несмещенной оценкой. n

 

Теорема 23.2. Арифметическая средняя , вычисленная по n независимым наблюдениям над случайной величиной x, которая  имеет Mx = m  и  ,  является состоятельной оценкой этого параметра.

 

Д о к а з а т е л ь с т в о.

 

          Пусть  - n независимых наблюдений над случайной величиной x. Тогда в силу теоремы 23.1 имеем Mx = .

          Для средней арифметической  запишем неравенство Чебышева:

                                         .

Используя свойства дисперсии 4,5 и (23.1), имеем:

                             ,

т.к. по условию теоремы .

Следовательно,

                    .                                                       (23.2)

          Итак, дисперсия средней арифметической в n раз меньше дисперсии случайной величины x. Тогда

                                              ,

поэтому

                                                ,

а это значит, что  является состоятельной оценкой.

 

З а м е ч а н и е : 1. Примем без доказательства весьма важный для практики результат. Если x Î N (a, s), то несмещенная оценка  математического ожидания a имеет минимальную дисперсию, равную , поэтому  является эффективной оценкой параметра а. n

         

Перейдем к оценке для дисперсии и проверим ее на состоятельность и несмещенность.

 

Теорема 23.3. Если случайная выборка состоит из n независимых наблюдений над случайной величиной  x с

 Mx = m  и  Dx = , то выборочная дисперсия

                                                                                         (23.3)

не является несмещенной оценкой Dx  - генеральной дисперсии.

 

Д о к а з а т е л ь с т в о.

 

          Пусть  - n независимых наблюдений над случайной величиной x. По условию  и  для всех . Преобразуем формулу (23.3) выборочной дисперсии:

 

          Упростим выражение

                                                .

Принимая во внимание (23.1), откуда

                                                           

можно записать

 

Тогда

         

Теперь рассмотрим  - математическое ожидание выборочной дисперсии:

                            

Используя определение дисперсии, получаем:

                            

                   и                     в силу (23.2), следовательно,

                             ,                                                  (23.4)

т.е. выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности.

         

З а м е ч а н и е 2. Оценку (23.4) можно исправить так, чтобы она стала несмещенной

                                                                                    (23.5)

Обычно оценку  называют исправленной выборочной дисперсией. Действительно,

                            

тогда

                  

          Дробь  называют поправкой Бесселя. При малых n  поправка Бесселя значительно отличается от 1. При n > 50 практически нет разницы между  и  .

          З а м е ч а н и е 3. Можно показать, что оценки  и  являются состоятельными и не являются эффективными.

          Несмещенной, состоятельной и эффективной оценкой  является оценка

                                                                                         (23.6)

в случае, когда математическое ожидание m известно.

 

Доверительные интервалы

         

Изучавшиеся ранее оценки неизвестного параметра являются точечными: мы старались судить о значении неизвестного числа или вектора q по значению оценки , принятом ею, как только известна статистическая выборка (). Однако, поскольку оценка сама является случайной величиной, её выборочное значение заведомо не совпадает с константой q. Имея в виду это обстоятельство, предпочтительнее стремиться указывать не точное значение оцениваемого параметра, а некоторый интервал, содержащий в себе значение параметра. Границы такого интервала должны определяться доступной нам информацией - выборкой из генеральной совокупности, то есть они сами случайны, и поэтому есть смысл говорить о вероятности того, что значение параметра находится внутри интервала.

 

Определение 24.1. Пусть генеральная совокупность описывается случайной величиной x, распределение которой зависит от скалярного параметра q. Пусть, далее,  и  две функции выборки такие, что всегда  и

                                      .

() со случайными границами называют доверительным интервалом для неизвестного параметра q с доверительной вероятностью b.

          Число a = 1-b называют уровнем значимости интервала.

          Стараясь иметь как можно более достоверные выводы, границы доверительного интервала выбирают таким образом, чтобы доверительная вероятность b была как можно ближе к 1.

          Схематически процесс построения доверительного интервала можно описать следующим образом.

          Пусть  - несмещенная оценка параметра q.

          Выберем доверительную вероятность b. Значение выражения «b как можно ближе к 1» относительно, оно находится вне границ математики и определяется лицом, производящим статистические исследования. Обычно выбирают b равным 0,9; 0,95; 0,99.

          Пусть, далее, можно найти такое число e > 0, что

                                                .                                          (24.1)

Записав  (24.1) в виде

,

видим, что интервал () является доверительным интервалом для параметра q с уровнем значимости a = 1-b.

          Практически вопрос о построении доверительного интервала связан с возможностью нахождения распределения оценки , а это, в свою очередь, зависит от распределения генеральной совокупности.

Пример 24.1. Построение доверительного интервала для математического ожидания нормальной генеральной совокупности при известной дисперсии.

          Пусть генеральная совокупность x распределена по нормальному закону с параметрами (q,s2), где s2 (дисперсия) известно. Мы уже знаем, что наилучшей в смысле несмещенности, состоятельности и эффективности оценкой неизвестного математического ожидания q нормального закона является выборочное среднее

.

          В продвинутом курсе теории вероятностей доказывается, что нормальное распределение обладает свойством устойчивости : если независимые случайные величины x, h распределены нормально с параметрами () и () соответственно, то их сумма x + h распределена нормально с параметрами ().

          Используя это утверждение в нашем случае, заключаем, что распределена нормально с параметрами (), а нормированное выборочное среднее  подчинено нормальному закону с параметрами (0,1).

          Это означает, что

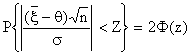,    где .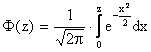

          Функция Ф(z) нам уже встречалась, её значения табулированы.

          Выберем теперь доверительную вероятность b и обозначим корень уравнения Ф() = b/2.

          После этого рассмотрим равенства

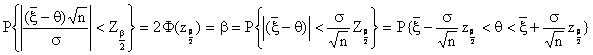, которые свидетельствуют о том, что интервал

является доверительным для параметра q с доверительной вероятностью b ( и уровнем значимости a = 1 - b).

          Приведем часть из таблицы значений  (прил. 2) для некоторых наиболее употребительных значений b.

 

Таблица 24.1 (Зависимость  от доверительной вероятности)

 

b

0,9

0,925

0,95

0,99

1,65

1,78

1,96

2,89

         

 

 

Обозначим  половину ширины доверительного интервала.

Замечаем, что:

1) при фиксированной доверительной вероятности b ширина доверительного интервала уменьшается с ростом числа наблюдений n как величина порядка   ( при увеличении, например, числа наблюдений в 100 раз ширина интервала уменьшится в 10 раз);

2) поскольку Ф(z) возрастает с ростом z, то увеличение доверительной вероятности, при всех прочих постоянных параметрах, приводит к расширению доверительного интервала.

          Пример 24.2. Желая узнать, сколько часов в неделю дети проводят у телевизора, социологическая служба обследовала 100 учеников некого города, в результате чего оказалось, что в среднем это число равно . Из прошлой практики известно, что стандартное отклонение () генеральной совокупности равно 6 (часов). Найдем доверительный интервал с доверительной вероятностью 0,95 для числа часов в неделю, проводимых ребенком у телевизора.

          Поскольку b = 0,95, из табл. 24.1 находим , и границы интервала доверия будут такими:

,

интервал доверия имеет вид (26.32; 28.68).

          Теперь поставим вопрос иначе: сколько детей надо обследовать с тем, чтобы среднее число часов в неделю, проводимых ребенком у телевизора, отклонилось от его оценки не более чем на 0,5 ч. с вероятностью 0,95?

          В такой постановке речь идет о нахождении числа n таким, чтобы выполнялось равенство

 ,

откуда  или n = (2sZ0.475)2.

          В условиях примера n = (2×6×1,96)2 @ 553.

          Разумеется, при больших значениях n ширина доверительного интервала уменьшится.

          Заметим, что по сравнению с первоначальной задачей ширина интервала уменьшилась в 1,18/0,5 = 2,36 раз, количество необходимых испытаний увеличилось в (2,36)2 = 5,57 раз ( 553 отличается в третьем знаке от 100 × 5,57).   u

 

Пример 24.3. Построение доверительного интервала для математического ожидания нормальной генеральной совокупности при неизвестной дисперсии.

          Снова рассмотрим генеральную совокупность x, распределенную нормально с параметрами (q,s2), однако теперь считаем дисперсию s2 неизвестной.

          Обозначим  стандартное выборочное квадратичное отклонение

.

          В курсах теории вероятностей доказывается, что случайная величина

подчиняется так называемому закону распределения Стьюдента с n - 1 степенью свободы и её плотность имеет вид

,

где Кn некоторая нормирующая константа.

          Созданы таблицы , дающие возможность вычислять вероятности вида

(см. прил. 4).

          Ввиду вышесказанного, получаем равенства:

,

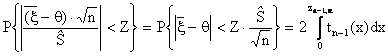из которых видно, что выбрав Z как корень уравнения

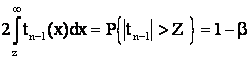
( обозначим этот корень ), приходим к доверительному интервалу для q вида

.   u

Пример 24.4. Рассмотрим вопрос о построении доверительного интервала для неизвестного количества времени в течение недели, проводимого ребенком у экрана телевизора, сохранив все данные примера 24.2, считая теперь, что 6ч. есть оценка выборочного среднеквадратического отклонения, .

          По таблице распределения Стьюдента (см. приложение 4) находим , границы интервала будут

,

а сам интервал (25,92; 29,08).

          Замечаем, что интервал стал шире, что объясняется уменьшением объема имеющейся информации из-за незнания ещё одного параметра генеральной совокупности.   u

 

Методы получения оценок

          До сих пор мы считали, что оценка неизвестного параметра известна и занимались изучением ее свойств с целью использования их при построении доверительного интервала. В этом параграфе рассмотрим вопрос о способах построения оценок.

            1. Метод моментов

          Пусть требуется оценить неизвестный параметр , вообще говоря, векторный, . При этом предполагается, что вид функции распределения известен с точностью до параметра ,

                                      .

          В таком случае все моменты случайной величины x становятся функциями от :

.

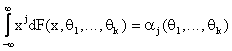          Метод моментов требует выполнения следующих действий:

1.   Вычисляем k «теоретических» моментов

.

2. По выборке  строим k одноименных выборочных моментов. В излагаемом контексте это будут моменты

3. Приравнивая «теоретические» и одноименные им выборочные моменты, приходим к системе уравнений относительно компонент оцениваемого параметра

                                                                           (25.1)

4. Решая полученную систему (точно или приближенно), находим исходные оценки . Они, конечно, являются функциями  от выборочных значений .

          Мы изложили порядок действий, исходя из начальных - теоретических и выборочных - моментов. Он сохраняется при ином выборе моментов, начальных, центральных или абсолютных, который определяется удобством решения системы (25.1) или ей подобной.

          Перейдем к рассмотрению примеров.

 

Пример 25.1. Пусть случайная величина x распределена равномерно на отрезке  [ a ;b ] , где  - неизвестные параметры. По выборке () объема n из распределения случайной величины x. Требуется оценить a и b .

 

 

Р е ш е н и е.

          В данном случае распределение определяется плотностью

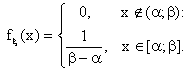
          1) Вычислим первые два начальных  «теоретических» момента:

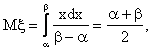
          2) Вычислим по выборке два первых начальных выборочных момента

 

          3) Составим систему уравнений

 

 

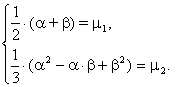
          4) Из первого уравнения выразим a через b

и подставим во второе уравнение, в результате чего придём к квадратному уравнению

решая которое, находим два корня

.

 

Соответствующие значения a таковы

.

          Поскольку по смыслу задачи должно выполнятся условие a < b , выбираем в качестве решения системы  и оценок неизвестных параметров

.

          Замечая, что есть не что иное, как выборочная дисперсия , получаем окончательно

.

          Если бы мы выбрали в качестве «теоретических» моментов математическое ожидание и дисперсию, , то пришли бы к системе (с учетом неравенства a < b)

которая линейна и решается проще предыдущей. Ответ, конечно, совпадает с уже полученным.   u

          Наконец, отметим, что наши системы всегда имеет решение и при том единственное. Полученные оценки, конечно, состоятельны, однако свойствам несмещенности не обладают.

 

            2. Метод максимального правдоподобия

          Изучается, как и прежде, случайная величина x, распределение которой задается либо вероятностями её значений , если x дискретна, либо плотностью распределения , если x непрерывна, где - неизвестный векторный параметр. Пусть () - выборка значений x. Естественно в качестве оценки  взять то значение параметра, при котором вероятность получения уже имеющейся выборки максимальна.

          Выражение

называют функцией правдоподобия, она представляет собой совместное распределение или совместную плотность случайного вектора с n независимыми координатами, каждая из которых имеет то же распределение (плотность), что и x.

          В качестве оценки неизвестного параметра  берется такое его значение , которое доставляет максимум функции , рассматриваемой как функции от  при фиксированных значениях . Оценку  называют оценкой максимального правдоподобия. Заметим, что  зависит от объема выборки n и выборочных значений

,

и, следовательно, сама является случайной величиной.

          Отыскание точки максимума функции представляет собой отдельную задачу, которая облегчается, если функция дифференцируема по параметру .

          В этом случае удобно вместо функции рассматривать её логарифм, поскольку точки экстремума функции и её логарифма совпадают.

          Методы дифференциального исчисления позволяют найти точки, подозрительные на экстремум, а затем выяснить, в какой из них достигается максимум.

          С этой целью рассматриваем вначале систему уравнений

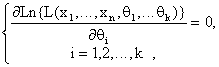                                                                        (25.2)

решения которой - точки, подозрительные на экстремум. Затем по известной методике, вычисляя значения вторых производных

по знаку определителя, составленного из этих значений, находим точку максимума.

Оценки, полученные по методу максимального правдоподобия, состоятельны, хотя могут оказаться смещенными.

          Рассмотрим примеры.

 

Пример 25.2.  Пусть производится некоторый случайный эксперимент, исходом которого может быть некоторое события А, вероятность Р(А) которого неизвестна и подлежит оцениванию.

          Р е ш е н и е.

          Введем случайную величину x равенством

 

                            

если событие А произошло,

если событие А не произошло (произошло событие ).

 

          Распределение случайной величины x задается равенством

          Выборкой в данном случае будет конечная последовательность (), где каждое из  может быть равно 0 либо 1.

          Функция правдоподобия будет иметь вид

          Найдем точку её максимума по р, для чего вычислим производную логарифма

 

Обозначим  - это число равно количеству единиц «успехов» в выбранной последовательности.

          Приравняем полученную производную к нулю

и решим полученное уравнение

.

 

Поскольку производная  меняет знак с «+» на «-» при возрастании р от 0 до 1, точка  есть точка максимума функции L, а  - оценка максимального правдоподобия параметра р. Заметим, что отношение  есть частота появления события А в первых n испытаниях.

          Поскольку m есть число «успехов» в последовательности n независимых испытаний ( в схеме Бернулли), то , и  - несмещенная оценка. В силу закона больших чисел Бернулли  стремится по вероятности к р, и оценка состоятельна.   u

 

Пример 25.3. Построим оценки неизвестных математического ожидания и дисперсии нормально распределенной случайной величины x с параметрами .

Р е ш е н и е.

          В условиях примера случайная величина определяется плотностью распределения

.

          Сразу выпишем логарифм функции правдоподобия

.

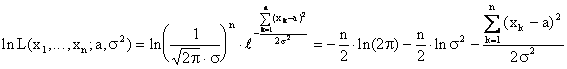          Составим систему уравнений для нахождения экстремальных точек

 

          Из первого уравнения находим , из второго, подставляя найденное значение â, находим .

          Вычислим вторые производные функции lnL в точке ():

А = ,           В = ,                С = .

          Поскольку определитель

,

а А < 0, то найденная точка в самом деле точка максимума функции правдоподобия.

          Заметим, что оценка  есть выборочное среднее (несмещенная и состоятельная оценка математического ожидания), а  - выборочная дисперсия (смещенная оценка дисперсии).   u