

Выберите нужную Вам работу
Тема: Функции нескольких переменных
Для выполнения работы необходимо усвоить теоретический материал:
1. Определение функции нескольких независимых переменных; основные понятия и обозначения;
2. Частные производные;
3. Полный дифференциал;
4. Экстремум функции нескольких переменных и его необходимые условия;
5. Понятие об эмпирических формулах;
6. Подбор параметров по методу наименьших квадратов.
Цель работы: Нахождение параметров приближенной зависимости между величинами методом наименьших квадратов
I. Вводные замечания
В различных исследованиях по данным результатов исследований, часто возникает необходимость построения эмпирических формул, составленных по этим наблюдениям.
Если аналитическое выражение функции неизвестно,
то возникает необходимость в решении практически важной задачи: найти
эмпирическую формулу ![]() значения
которой при х = хі
мало отличались бы от опытных данных
уі.
значения
которой при х = хі
мало отличались бы от опытных данных
уі.
Пусть произвели ряд измерений х и у. В результате полученные данные записаны в таблицу значений
хi
x1
x2
x3
...
xn
уi
y1
y2
y3
...
yn
|
|
Геометрически задача построения эмпирической формулы состоит в проведении кривой, «возможно ближе» примыкающей к системе точек Аі(хі,уі) (см. Рис.1).
Рис.1.
Построение эмпирической формулы слагается из двух этапов:
1) выяснение общего вида этой формулы;
2) определение наилучших параметров ее.
Большое значение для удачного подбора формулы имеет геометрическое изображение полученных данных в декартовых координатах или в специальных системах координат. По положению точек можно высказать предположение об общем виде зависимости на основе сходства между построенным графиком и образцами известных кривых.
Если вид эмпирической функции формулы выбран, то возникает задача определения наилучших коэффициентов (параметров), входящих в эту формулу.
Пусть данная система значений Аi(xi,yi) (i = 1,2, …, n) приближенно описывается формулой вида:
![]() ,
(1)
,
(1)
где
f
– известная функция, а ![]() -
неизвестные параметры (постоянные), число которых обычно меньше числа точек Аi
, т.е. n
< k.
Требуется определить эти постоянные. Если (xi,yi)
точно связаны зависимостью (1), то параметры
-
неизвестные параметры (постоянные), число которых обычно меньше числа точек Аi
, т.е. n
< k.
Требуется определить эти постоянные. Если (xi,yi)
точно связаны зависимостью (1), то параметры ![]() могут
быть найдены из системы уравнений
могут
быть найдены из системы уравнений
![]() .
(2)
.
(2)
Но на практике значения (xi,yi)
содержат неизбежные ошибки, а число уравнений (2) больше числа неизвестных и
система (2), как правило, несовместна. Поэтому находят наилучшие значения
(оценки) ![]() ,
приближенно удовлетворяющие системе (2) так, что невязки (уклонения)
,
приближенно удовлетворяющие системе (2) так, что невязки (уклонения)
![]()
являются, возможно, малыми по абсолютной величине.
Наиболее часто применяются методы:
1) метод выбранных точек,
2) метод средних,
3) метод наименьших квадратов.
Одним из наилучших способов получения таких формул является метод (способ) наименьших квадратов.
II. Описание метода (наименьших квадратов)
Пусть по результатам опыта нам нужно установить зависимость между двумя величинами х и у, где, например,
х - накладные расходы;
у - стоимость строительства объекта.
По результатам наблюдения составим таблицу:
хi
x1
x2
x3
...
xn
уi
y1
y2
y3
...
yn
Нужно теперь установить функциональную зависимость у = f(x).
Нанесем результаты наблюдений на координатную плоскость.

В данном случае естественно предположить, что зависимость линейная (т.е. все точки расположены около прямой).
Т.е. у = ах + b,
(*)
где а и b - некоторые постоянные коэффициенты, подлежащие определению.
Представим (*) в виде
ах + b - y = 0 (**)
Так как точки лежат приблизительно на этой прямой, то эта зависимость приближенная. И, если подставить точки наблюдений в (**), то получим равенства:
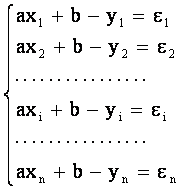 (3)
(3)
где числа ei (i = 1¸n) называются погрешностями и, вообще говоря, не равные нулю.
Способ наименьших квадратов состоит в том, что нужно подобрать а и b таким образом, чтобы ei были бы по возможности малыми по абсолютной величине, а лучше сказать, чтобы сумма квадратов погрешностей была бы минимальной. Т.е. потребуем, чтобы
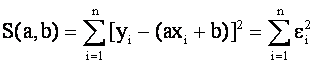 (4)
(4)
тогда S(a,в) можно рассматривать как функцию двух переменных по а и b и можно ее исследовать на экстремум ( определить минимум), т.е.
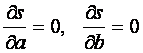 .
.
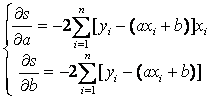 (5)
(5)![]()
Приравняем эти частные производные к нулю, получаем линейную систему двух уравнений с двумя неизвестными а и b :
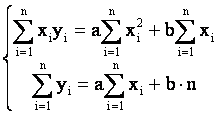 (6)
(6)
Система (6) называется нормальной системой способа наименьших квадратов.
Решая эту систему относительно а и b, находим числа а и b. Затем подставляем их в (*) получим линейную функцию, наилучшим образом отражающую зависимость между величинами х и у, полученную на основании наблюдений (из опыта).
Если опытные данные таковы, что при нанесении точек они примерно располагаются по квадратной параболе, то аналогично нужно искать приближенную зависимость в виде
у = ах2 + bx +c.
И теперь из условия минимума функции трех переменных находим оценки параметров S(a,b,c). Линейная система (6) будет состоять их трех уравнений первой степени.
III. Ход выполнения лабораторной работы
1. З а д а н и е. Дана таблица значений некоторой функции при различных значения аргумента, найти эмпирическую формулу у = f(x) данной зависимости.
2. Для определения вида формулы, нанесите наблюдения на декартову систему координат (постройте график эмпирической таблицы). Используйте ЭВМ (например, excel).
3. Сравнивая, полученный точечный график с разными кривыми, уравнения которых известны, выберите вид эмпирической формулы.
4. Определите оценки коэффициентов, входящих в эту формулу по методу наименьших квадратов (можно воспользоваться ЭВМ: любым пакетом программ «Аппроксимация опытных данных методом наименьших квадратов»).
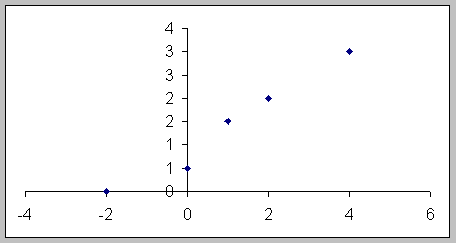
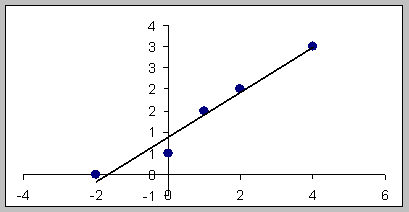
Пример. Пусть имеем результаты наблюдений:
|
хi |
-2 |
0 |
1 |
2 |
4 |
|
уi |
0.5 |
1 |
1.5 |
2 |
3 |
График эмпирической таблицы имеет вид
Определим а и b в уравнении у = ах + b
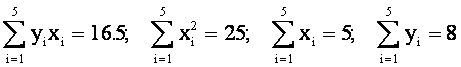
Нормальная система
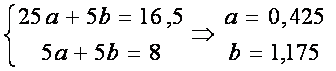 .
.
Тогда у = 0,425х + 1,175.
Нанесем график на поле точек
Тема: Определенный интеграл
Для выполнения работы необходимо усвоить теоретический материал:
7. Что называется интегральной сумой данной функции у = f(x) на данном отрезке [a,b];
8. Что называется определенным интегралом данной функции у = f(x) на данном отрезке [a,b]. Его основные свойства и геометрический смысл;
9. Какие геометрические величины можно вычислять с помощью определенного интеграла;
10. Методы приближенного вычисления определенного интеграла:
а) метод прямоугольников;
б) метод трапеций;
в) метод Симпсона.
Цель работы: Освоение методов численного интегрирования
I. Вводные замечания
Когда возникает задача численного интегрирования? Для этого вспомним теорему Коши:
Теорема (Коши). Всякая непрерывная функция имеет первообразную. То есть пусть f(x) - непрерывна, определена на (a,b) Þ $ F(x) : F/(x) = f(x) и тогда
![]() .
.
Замечание. Но, тем не менее, не решается вопрос о том, как найти первообразную с помощью конечного числа известных операций над элементарными функциями. Более того, имеется ряд непрерывных элементарных функций, интегралы от которых не являются элементарными функциями. Такие интегралы называются “неберущимися”.
Под численным интегрированием понимают нахождение приближенного значения определенного интеграла
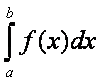 .
(1)
.
(1)
Приближенные методы приходится применять из-за того, что первообразную для f(x) нельзя выразить через элементарные функции или отыскание ее сопряжено со значительными трудностями.
Для получения приближенного значения интеграла (1) функцию f(x) аппроксимируют, т.е. приближенно выражают через другую функцию, более простую, функцией j(х) и принимают
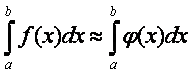 .
.
II. Описание методов
1. Понятие об интерполяции
Интерполяция – это построение приближенной или точной аналитической формулы у = j(х), если известны значения уі в дискретном ряде хі.
|
хi |
x0 |
x1 |
х2 |
... |
xn |
|
уi |
у0 |
y1 |
у2 |
... |
yn |
Точки хі (і = 0,1,2. ..., n) называют узлами.
Среди элементарных функций самыми простыми являются многочлены и поэтому часто данную функцию у = f(x) аппроксимируют многочленом возможно низшей степени m, Pm(x) таким, чтобы
Pm(x) = уі, (і = 0,1,2. ..., n).
Многочлен Pm(x) может быть построен единственным способом при
m = n и называется интерполяционным многочленом Лагранжа
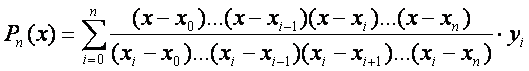 .
.
Рассмотрим два важнейших случая:
а). Линейная интерполяция:
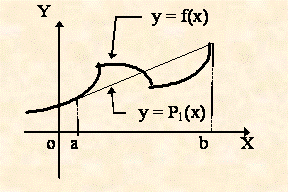 f(x)
»
P1(x);
f(x)
»
P1(x);
х0 = а, у0 = f(x0);
х1 = b, у1 = f(x1);
у0 = P(x0), у1 = P(x1).
Интерполяционный многочлен Лагранжа будет иметь вид:
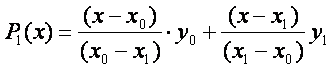 .
(2)
.
(2)
б). Параболическая интерполяция:
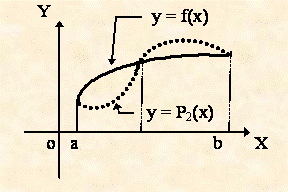 f(x)
»
P2(x);
f(x)
»
P2(x);
х0 = а, у0 = f(x0);
х1 = (а+b)/2, у1 = f(x1);
х2 = b, у2 = f(x2).
Интерполяционный многочлен Лагранжа будет иметь вид:
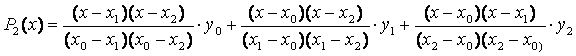 .
(3)
.
(3)
Замечание. Отметим, что совпадение интерполяционного многочлена Pn(x) и функции f(x) в узлах хі (і = 0,1,2. ..., n) не означает их совпадения в остальных точках промежутка [a,b], поэтому всегда необходимо оценивать погрешность замены f(x) ее интерполяционным многочленом.
Разность Rn(x) = f(x) - Pn(x) называется остаточным членом.
Применяя теорему Ролля можно получить оценку остаточного члена, которая будет иметь вид:
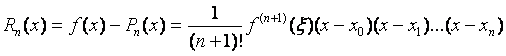 ,
(4)
,
(4)
где x Î (a,b).
2. Метод прямоугольников
Для получения приближенного значения интеграла (1) можно использовать геометрический смысл определенного интеграла.
Пусть у = f(x) определена на [a,b], непрерывна и нужно определить площадь, ограниченную кривой y = f(x), а также прямыми х = а, х = b, y = 0.
|
|
Si(x) = f(xi)×Dxi,
где Dхi = хi - хi-1.
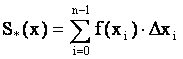 .
.
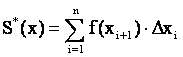 .
.
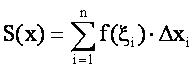 .
.
Тогда имеем ![]() .
.
Устремим n ® ¥, Dxi ® 0. Возьмем
![]() .
.
 .
.
Но тогда
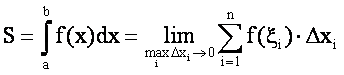 .
.
Таким образом, определенный интеграл от непрерывной неотрицательной функции при a £ b равен площади соответствующей криволинейной трапеции.
На основании этого имеем приближенную формулу:
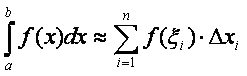 .
(5)
.
(5)
3. Метод трапеций
Пусть необходимо вычислить
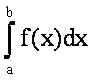 .
.
Воспользуемся геометрическим смыслом или, что тоже самое, аппроксимируем f(x) на [a,b] многочленом (2) получим приближенную формулу для вычисления интеграла.
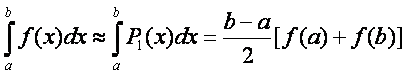 .
(6)
.
(6)
Здесь площадь криволинейной трапеции заменяется
площадью трапеции. Погрешность формулы трапеций (6) бывает очень велика.
Для увеличения точности разобьем отрезок
[a,b]
на n равных частей длиной ![]() (
h - шаг разбиения) и в каждой части применим формулу (6).
(
h - шаг разбиения) и в каждой части применим формулу (6).
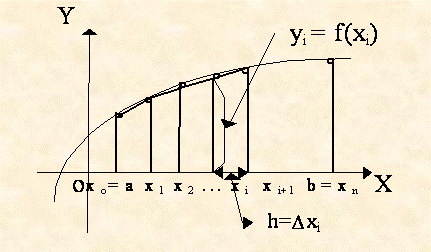
Тогда узловые точки разбиения хi = х0 + i×h, a yi = f(xi), i = 0,1, ... , n дадут нам n трапеций с основаниями yi = f(xi) и высотой h.
Суммируя площади этих трапеций, будем иметь обобщенную формулу трапеций для вычисления приближенного интеграла
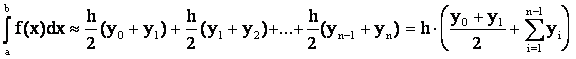 .
(7)
.
(7)
Замечание. Погрешность этой формулы (7) можно определить используя (4)
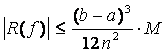 ,
где
,
где ![]() .
.
4. Метод Симпсона
Иногда лучшее приближение дает другая формула, профиль криволинейной трапеции полоски (трапеции) считать параболическим.
Интерполируя функцию f(x) по формуле (3) и выполнив интегрирование, получим малую формулу Симпсона (формула парабол).
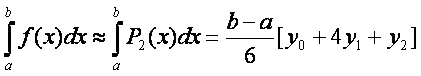 .
(8)
.
(8)
Можно показать, что погрешность этой формулы определяется по формуле
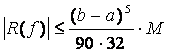 ,
где
,
где ![]() .
.
Для увеличения точности разобьем отрезок [a,b] на n =2×m частей.
|
|
И на каждом участке аппроксимируем нашу кривую
y = f(x) параболой
|
|
y = A×x2 + B×x + C.
Например, если h мало, то кривую y = f(x) можно заменить параболой
y = A×x2 + B×x + C, проходящей через точки М(х0,у0), L(x1,y1), D(x2,y2). Но нам нужно определить коэффициенты А,В,С для параболы.
С одной стороны
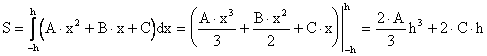 .
.
С другой стороны, если х0 = -h, тогда A×h2 - B×h + C = y0,
при x1 = 0 получаем C = y1,
и x2 = h - A×h2 + B×h + C = y2
то есть y1 = C, a ![]() .
Тогда подставим полученные значения в (5.4), получим
.
Тогда подставим полученные значения в (5.4), получим
 .
.
Но так мы можем аппроксимировать на любом промежутке [a,b] любого разбиения т.е. интерполируя функцию f(x) по формуле (3) и выполнив интегрирование, получим
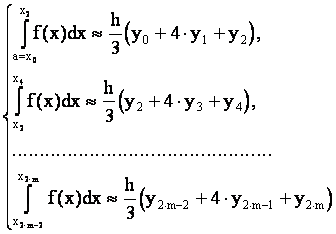 .
.
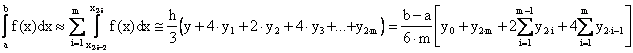
(9)
(Обобщенная формула Симпсона)
Погрешность формулы оценивается так
 ,
где
,
где ![]() .
.
III. Ход выполнения лабораторной работы
З а д а н и е.
Вычислить  приближенно,
используя методы 2,3,4 по обобщенным формулам (5), (7), (9) с абсолютной
точностью çR(f)ç
£
0,01.
приближенно,
используя методы 2,3,4 по обобщенным формулам (5), (7), (9) с абсолютной
точностью çR(f)ç
£
0,01.
Полученные результаты сравнить и сделать выводы. Используйте ЭВМ (например, excel)
Постройте графики подынтегральных функций y = f(x).
Тема: Ряды
Для выполнения работы необходимо усвоить теоретический материал:
11. Что называется сумой сходящегося числового ряда?
12. Почему при исследовании сходимости ряда можно отбрасывать любое конечное начальных членов ряда?
13. Предел общего члена ряда равен нулю, можно утверждать, что ряд сходится?
14. Изучите теорему сравнения рядов;
15. В чем суть метода Даламбера сходимости ряда;
16. Какие числовые знакопеременные ряды называются абсолютно сходящимися и, какие условно сходящимися? Приведите примеры;
17. В чем состоит признак Лейбница сходимости рядов?
18. Понятие степенного ряда. Рассмотрите степенные ряды, имеющие нулевой, конечный и бесконечный радиус сходимости;
19. Для каких значений х справедливы разложения в ряд функций:
а) у = ℮х;
б) у = Sinx;
в) ln(1+x)?
Цель работы: Исследование рядов на сходимость. Вычисления суммы ряда
I. Вводные замечания
Рассмотрим числовой ряд ![]() .
Необходимо установить сходимость ряда, если ряд сходится, то вычислить сумму с
некоторой точностью
e.
.
Необходимо установить сходимость ряда, если ряд сходится, то вычислить сумму с
некоторой точностью
e.
Исследование числового ряда целесообразно
начинать с проверки необходимого условия сходимости ряда, именно с
проверки условия ![]() ,
где аn
– общий член ряда. Если условие не выполнено, т.е. либо предел
,
где аn
– общий член ряда. Если условие не выполнено, т.е. либо предел ![]() не
существует, либо он бесконечен, либо конечен, но равен 0, то ряд
не
существует, либо он бесконечен, либо конечен, но равен 0, то ряд ![]() расходится.
Если же для ряда
расходится.
Если же для ряда ![]()
![]() ,
то вопрос о сходимости остается открытым, и требуются дополнительные
исследования на сходимость.
,
то вопрос о сходимости остается открытым, и требуются дополнительные
исследования на сходимость.
Продемонстрируем это на примерах.
З а д а ч а 1.
Исследовать на сходимость ряд ![]() .
.
Р е ш е н и е. Проверим необходимое условие,
![]() (этот
придел не существует), а
(этот
придел не существует), а ![]() .
Необходимое условие не выполнено. Следовательно, данный ряд расходится.
.
Необходимое условие не выполнено. Следовательно, данный ряд расходится.
Теперь покажем применение основных достаточных признаков сходимости рядов (признак сравнения, признак Даламбера, признак Коши, интегральный признак).
З а д а ч а 2.
Исследовать на сходимость ряд ![]() .
.
Р е ш е н и е. Проверим необходимое условие,
общий член ряда ![]() ,
тогда
,
тогда ![]()
следовательно оно выполнено. Для доказательства
сходимости применим достаточный признак сравнения рядов. Рассмотрим ряд с общим
членом ![]() и
исследуем его на сходимость: а) Так как
и
исследуем его на сходимость: а) Так как ![]() ,
то необходимое условие выполнено.
,
то необходимое условие выполнено.
Для проверки сходимости ряда ![]() применим
интегральный признак сходимости рядов. Здесь
применим
интегральный признак сходимости рядов. Здесь ![]() тогда
тогда
![]() ,
а так как производная
,
а так как производная ![]() для
всех х Î
[2,¥),
то
для
всех х Î
[2,¥),
то ![]() убывает
на [2,¥).
Все условия
убывает
на [2,¥).
Все условия
интегрального признака выполнены. Тогда для
доказательства нужно вычислить интеграл![]() .
Интеграл расходится, но тогда и ряд
.
Интеграл расходится, но тогда и ряд ![]() тоже
расходится. Теперь применим предельный признак сравнения рядов
тоже
расходится. Теперь применим предельный признак сравнения рядов  .
Видим, что предел конечен и отличен от нуля, а так как ряд
.
Видим, что предел конечен и отличен от нуля, а так как ряд ![]() расходится,
то и
расходится,
то и
ряд ![]() будет
расходящимся.
будет
расходящимся.
Достаточные признаки Коши и Даламбера
проиллюстрируем при исследовании степенных рядов. Ели проанализировать
доказательство признака Даламбера, то можно заметить, что для ряда с
положительными членами ![]() существует
предел
существует
предел ![]() .
Если l
< 1, то ряд сходится, а при
l
> 1 общий член ряда не стремится к нулю и, следовательно, ряд расходится.
Аналогичным образом можно сформулировать признак Коши.
.
Если l
< 1, то ряд сходится, а при
l
> 1 общий член ряда не стремится к нулю и, следовательно, ряд расходится.
Аналогичным образом можно сформулировать признак Коши.
З а д а ч а 3.
Найти область сходимости степенного ряда ![]() .
.
Р е ш е н и е. Применим признак Даламбера к данному ряду:
![]() ;
рассмотрим предел отношения
;
рассмотрим предел отношения
 .
.
Тогда ряд ![]() будет
сходящимся, если будет сходится ряд
будет
сходящимся, если будет сходится ряд  ,
но это возможно, в силу признака Даламбера, если
,
но это возможно, в силу признака Даламбера, если ![]() т.е.,
если
т.е.,
если ![]() или
-8 < x
< 10.
или
-8 < x
< 10.
А при
x
< -8 и x
>10 ряды  и
и
![]() будут
расходящимися т.к. для всех значений х
Î(-¥;
-8) È
(10; ¥)
будут
расходящимися т.к. для всех значений х
Î(-¥;
-8) È
(10; ¥)
общий член ряда un не стремится к нулю.
Напомним, что из расходимости ряда ![]() ,
вообще говоря, не следует расходимость ряда
,
вообще говоря, не следует расходимость ряда ![]() (см.
пример, где
(см.
пример, где ![]() ).
).
Поэтому необходимо исследовать сходимость
данного ряда на концах интервала сходимости т.е. при х = -8 ряд ![]() в
силу признака Лейбница будет сходящимся, а при х = 10 получим ряд
в
силу признака Лейбница будет сходящимся, а при х = 10 получим ряд ![]()
гармонический, который расходится. Итак,
областью сходимости степенного ряда![]() является промежуток [-8; 10).
является промежуток [-8; 10).
З а д а ч а 4.
Найти область сходимости степенного ряда  .
.
Р е ш е н и е. Для исследования ряда применим
признак сходимости Коши к ряду ![]() ,
полагая
,
полагая  .
Тогда
.
Тогда  ;
;

Далее рассуждения аналогичны задачи 3. Получим, что ряд сходится на отрезке [-3; -1]. В этом примере вопрос о сходимости ряда на концах интервала решен без дополнительного исследования.
Теория рядов часто применяется для приближенных вычислений значений функций и определенных интегралов. При этом следует обратить особое внимание на то, как оценить погрешность при замене суммы знакочередующегося ряда его частичной суммой. Если знакочередующийся ряд удовлетворяет условиям теоремы Лейбница, то допускаемая погрешность не превосходит по абсолютной величине первого из отброшенных членов ряда.
З а д а ч а 5.
Вычислить ![]() с
точностью 0,001.
с
точностью 0,001.
Р е ш е н и е. Представим ![]() .
.
Теперь воспользуемся разложением
 .
.
Положим ![]() получим
получим
![]()
![]()
Получаем с точностью до 0,001 ![]()
Условия признака Лейбница выполнены и поэтому допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов:
![]() .
.
Итак, ![]()
Рассмотрим числовой ряд ![]() для
которого требуется вычислить сумму
S
с некоторой точностью
e.
Заменяя S
суммой конечного числа членов ряда
Sn
при этом допускаем погрешность, равную остаточному члену
Rn,
где
для
которого требуется вычислить сумму
S
с некоторой точностью
e.
Заменяя S
суммой конечного числа членов ряда
Sn
при этом допускаем погрешность, равную остаточному члену
Rn,
где
Rn = S - Sn .
Для обеспечения заданной точности вычисления e необходимо потребовать, чтобы ç Rn ç < e.
Рассмотрим сущность метода Куммера.
Говорят, что ряд ![]() (*)
сходится медленно, если для получения его суммы
Sn
с точностью
e
нужно взять большое число его членов. Но есть другой ряд сходящийся быстрее
данного ряда (*) т.е. есть два сходящихся ряда
(*)
сходится медленно, если для получения его суммы
Sn
с точностью
e
нужно взять большое число его членов. Но есть другой ряд сходящийся быстрее
данного ряда (*) т.е. есть два сходящихся ряда ![]() и
и
![]() причем,
причем,
![]() ,
тогда bn
= o(an)
при n®¥
в этом случае говорят, что ряд
,
тогда bn
= o(an)
при n®¥
в этом случае говорят, что ряд ![]() сходится
быстрее ряда
сходится
быстрее ряда ![]() .
Сущность метода Куммера и заключается в том, чтобы данный ряд
.
Сущность метода Куммера и заключается в том, чтобы данный ряд ![]() заменить
рядом сходящимся быстрее, а именно
заменить
рядом сходящимся быстрее, а именно![]() .
.
II. Описание метода
Пусть ряд ![]() сходится
и сумма его равна S.
Подберем ряд
сходится
и сумма его равна S.
Подберем ряд ![]() сумма
которого известна S1,
причем,
сумма
которого известна S1,
причем, ![]() .
.
Представим ряд ![]() в
виде
в
виде
 .
.
Так как  т.е.
т.е.
![]() ,
то ряд
,
то ряд  сходится
быстрее ряда
сходится
быстрее ряда ![]() и
поэтому, вычисляя S
по формуле
и
поэтому, вычисляя S
по формуле
 ,
,
получаем требуемую точность e при меньшем числе членов.
В качестве рядов ![]() -
вспомогательных рядов с известными суммами можно использовать следующие ряды:
-
вспомогательных рядов с известными суммами можно использовать следующие ряды:
III. Ход выполнения лабораторной работы
З а д а н и е. Применяя метод Куммера
убыстрения сходимости рядов, вычислить сумму ряда ![]() с
точностью e.
с
точностью e.
Выполнение лабораторной работы необходимо разбить на несколько этапов:
1. Если величина, которую нужно вычислять, не представлена числовым рядом, нужно получить это представление (см. Зад. 5).
2. Исследовать ряд на сходимость следуя задачам 1- 4.
3. Определить количество членов ряда n, необходимое для обеспечения заданной точности e.
4.
Подобрать вспомогательный ряд ![]() из
таблицы п.II
такой, чтобы
из
таблицы п.II
такой, чтобы ![]() .
.
5.
Представить заданный ряд ![]() в
виде
в
виде  ,
где
,
где ![]() .
.
6.
Определить количество членов ряда  ,
необходимое для обеспечения заданной точности
e.
,
необходимое для обеспечения заданной точности
e.
7.
Вычислить сумму ряда ![]() с
точностью e.
с
точностью e.
П р и м е р. Вычислить сумму ряда
![]()
с точностью e = 10-6, применяя метод Куммера.
Р е ш е н и е. Сходимость ряда проверить самостоятельно.
Определим количество членов, необходимое для обеспечения требуемой точности e = 10-6 .

Решая последнее неравенство, получим
k + 1 > 10-6 , k > 10-6 - 1.
Итак, для обеспечения точности e = 10-6 необходимо взять примерно106 членов ряда.
Теперь воспользуемся вспомогательным рядом из таблицы
![]() =
=
![]() при
х = 2
при
х = 2
имеем
![]() =
=
![]() .
.
Находим
![]()
Отсюда

Определим количество членов полученного ряда, необходимое для обеспечения точности e.
 .
.
Откуда находим, что k ³ 10.
Таким образом,

Вычисление полученной суммы можно произвести на ЭВМ.
Тема: Элементы линейной алгебры
Для выполнения работы необходимо усвоить теоретический материал:
20. Что называется матрицей?
21. Какие действия (операции) установлены над матрицами? Как они определяются и каковы их свойства?
22. Определение обратной матрицы для данной матрицы А, всегда ли она существует и как ее найти?
23. Что называется определителем матрицы, для каких матриц он определен и какими свойствами обладает?
24. Что называется матрицей (расширенной матрицей) системы линейных уравнений?
25. Какие способы решения систем линейных уравнений Вы знаете? Опишите: а) метод Крамера;
б) матричный метод;
в) метод Гаусса.
26. Что такое ранг матрицы?
27. Условие совместимости систем линейных уравнений;
28. Определение линейного пространства. Что называется вектором?
29. Дайте определение линейной зависимости и независимости системы векторов;
30. Что называется размерностью линейного пространства?
31. Что называется базисом линейного пространства и координатами вектора в данном базисе?
32. Что называется арифметическим n-мерным пространством? При каком условии арифметическое n-мерное пространство Rn является линейным пространством?
33. Коков признак того, что данная система векторов в Rn является линейным пространством?
34. Собственные векторы неотрицательных матриц.
Цель работы: Использование теории матриц и определителей для решения задач линейной алгебры
I. Вводные замечания
Понятие матрицы играет важную роль во многих вопросах как теоретического, так и прикладного характера. Матрица (таблица) с m строками и n столбцами образуют, например, коэффициенты aij системы m линейных уравнений с n переменными (неизвестными); если к этой матрице добавить столбец свободных членов bi, то получим матрицу, определяющую систему уравнений (расширенная матрица. Другим примером матрицы может служить план перевозок некоторой продукции с m баз В1, В2, …, Вm n потребителям А1, А2, …, Аn: если обозначить xij – количество продукции, перевозимой с базы Вi потребителю Аj, то совокупность этих величин образует матрицу с m строками и n столбцами.
Теория определителей и систем линейных уравнений является частью линейной алгебры – математической дисциплины, которая в настоящее время широко применяется в решении и исследовании многих теоретических вопросов, как в самой математике, так и в решении практических вопросов.
Теория систем линейных уравнений закладывает основу большому и важному разделу алгебры - линейной алгебре.
Пусть нам дана система из n уравнений с n неизвестными
 (1)
(1)
Здесь х1, х2, ..., хn - неизвестные. Все они в первой степени (поэтому система называется линейной), а коэффициент i-го уравнения при j-том неизвестном обозначается через aij и bi - свободный член i-го уравнения.
Коэффициенты при неизвестных составляют прямоугольную таблицу
 ,
(2)
,
(2)
которая называется матрицей из n строк и n столбцов. Еще эту таблицу называют квадратной матрицей.
 ,
,
 (3)
(3)
b и x называются соответственно матрица-вектор b свободных членов и матрица-вектор х неизвестных.
Теперь (1) можно записать в виде
Ах = b (4)
Решением системы линейных уравнений (1) (а также (4), так как это эквивалентные записи) называется система n чисел k1,k2,...,kn таких, что каждое из уравнений (1) обращается в тождество после замены хi на ki.
Если система линейных уравнений не имеет ни одного решения, то она несовместна. В противном случае она называется совместной.
Система называется определенной, если она обладает одним единственным решением, и неопределенной, если решений больше, чем одно.
Задача теории систем линейных уравнений состоит в разработке методов, позволяющих узнать, совместна данная система уравнений или нет, и если совместна, то установить число решений, а также указать способ нахождения всех решений.
II. Описание методов
1. Формулы Крамера
Если матрица системы (1) А - квадратная, то есть
![]() ,
то она имеет определитель (детерминант):
,
то она имеет определитель (детерминант):
 .
.
З а м е ч а н и е. Не нужно смешивать эти два понятия. Матрица - это упорядоченное множество чисел, представленное в форме таблицы, а detA - число, вычисленное по определенной формуле:
![]() ,
,
где сумма берется по всем возможным комбинациям (a1,a2,...,an) элементов 1, 2, ..., n , а всего n! членов.
Введем в рассмотрение определители:
 (j
= 1, 2, …, n),
(j
= 1, 2, …, n),
получающиеся из определителя D заменой его j–го столбца (столбца коэффициентов системы при неизвестном хj) столбцом свободных членов.
Тогда верна следующая теорема:
Теорема. Если определитель системы D ¹ 0, то система уравнений (1) имеет единственное решение, и оно определяется по формулам Крамера:
 ,
(j
= 1, 2, …, n).
(5)
,
(j
= 1, 2, …, n).
(5)
Продемонстрируем это на примерах.
З а д а ч а 1. Решить систему уравнений по правилу Крамера (5)

Р е ш е н и е.
Вычислим определитель системы, если D ¹ 0, то данная система уравнений имеет единственное решение, и его можно будет определить по формулам Крамера.

Для вычисления определителя использовались основные свойства и преобразования.
Далее, аналогично определим




По формулам Крамера находим единственное решение системы:




О т в е т. х1 = 2, х2 = -3, х3 = 0, х4 = 4.
2. Метод Гаусса (метод исключения неизвестных)
Чтобы упростить изложение метода, рассмотрим систему из четырех уравнений и четырех неизвестных. Считаем, что система совместна.
 (1)
(1)
Ø. Пусть а11 ¹ 0 (ведущий коэффициент). Тогда разделим все члены первого уравнения на а11:
х1 + b12×x2 + b13×x3 + b14×x4 = b15, (2)
где
 ,
(j > 1).
,
(j > 1).
Полученное уравнение (2) умножим на а21, получим (*)
а21×х1 + а21×b12×x2 + a21×b13×x3 + a21×b14×x4 = a21×b15.
Это уравнение вычтем из второго уравнения исходной системы (2):
 .
.
В результате имеем
![]()
Повторим такую операцию со всеми оставшимися уравнениями. В результате получим систему
 (3)
(3)
Здесь
![]() ,
(i,j ³
2) (4)
,
(i,j ³
2) (4)
Ù.
Считаем, что в системе (3) ведущий элемент ![]() .
.
Повторим этап Ø.
![]() ,
(5)
,
(5)
где
 ,
(j > 2).
,
(j > 2).
Повторим процедуру (*) из этапа Ø. В результате получим систему, но уже без х2
 ,
(6)
,
(6)
где
![]() ,
(i,j ³
3) (7)
,
(i,j ³
3) (7)
Ú.
Теперь считаем, что ![]() ,
и аналогичным образом приходим к уравнению
,
и аналогичным образом приходим к уравнению
![]() ,
(8)
,
(8)
 (j
> 3).
(j
> 3).
Получим систему из одного уравнения
![]() ,
(9)
,
(9)
Û.
Пусть теперь ![]() .
Тогда
.
Тогда
![]() ,
(i,j ³
4). (10)
,
(i,j ³
4). (10)
Теперь
 .
(11)
.
(11)
И так далее, если работаем с системой более, чем из 4-х уравнений.
Эта часть вычислений называется прямым ходом метода Гаусса. Таким способом мы получим приведенные уравнения
 .
.
Из них мы последовательно находим неизвестные (обратный ход)
 .
(12)
.
(12)
З а м е ч а н и е
. Если ![]() на
каком-либо этапе окажется равным нулю, то уравнения системы надо переставить
надлежащим образом.
на
каком-либо этапе окажется равным нулю, то уравнения системы надо переставить
надлежащим образом.
При решении системы уравнений удобно результаты вычислений заносить в следующую таблицу:
Таблица №1.
|
х1
|
х2 |
х3
|
х4 |
свободный член |
S |
Этапы |
|
а11 а21 а31 а41 |
a12 a22 a32 a42 |
a13 a23 a33 a43 |
a14 a24 a34 a44 |
a15 a25 a35 a45 |
a16 a26 a36 a46 |
А0 |
|
1 |
b12 |
b13 |
b14 |
b15 |
b16 |
|
|
|
a(1)22 a(1)32 a(1)42 |
a(1)23 a(1)33 a(1)43 |
a(1)24 a(1)34 a(1)44 |
a(1)25 a(1)35 a(1)45 |
a(1)26 a(1)36 a(1)46 |
А1 |
|
|
1 |
b(1)13 |
b(1)14 |
b(1)15 |
b(1)16 |
|
|
|
|
a(2)33 a(12)43 |
a(2)34 a(2)44 |
a(2)34 a(2)44 |
a(2)36 a(2)46 |
A2 |
|
|
|
1 |
b(2)14 |
b(2)15 |
b(2)16 |
|
|
|
|
|
|
a(3)44 |
a(3)46 |
А3 |
|
|
|
|
1 |
b(3)15 |
b(3)16 |
|
|
1 |
1 |
1
|
1
|
x4 x3 x2 x1 |
|
В |
Для проверки вычислений полезно использовать “контрольные суммы”:
 (i
=1, 2, ..., 5)
(i
=1, 2, ..., 5)
 .
.
З а д а ч а 2. Решить систему методом Гаусса.

Р е ш е н и е.
Применим описанный выше метод.
Применение его приведет нас к следующей таблице:
|
х |
х |
х |
х |
S |
|
|
2 3 4 1 |
-3 4 2 1.5 |
4 -2 3 2 |
20 -11 9 10 |
23 -6 18 11.5 |
А0 |
|
|
8.5 8 1 |
-8 -5 -0.63 |
-41 -31 -3.87 |
-40.5 -28 -3.5 |
А1 |
|
|
|
-2.69 1 |
-8.07 3 |
-10.75 4 |
А2 |
|
1 |
1 |
1 |
3 -2 1 |
4 -1 2 |
В
|
О т в е т. х1 = 1, х2 = -2, х3 = 3.
Метод, изложенный выше, весьма прост и без труда реализуется на ЭВМ, однако он не дает возможности сформулировать условия совместимости или определенности системы при помощи коэффициентов и свободных членов этой системы.
Поэтому теорию развивают другим методом.
3. Метод обратной матрицы
Пусть система (1) задана в матричном виде (4):
Ах = b.
Введем определение обратной матрицы.
Определение. Матрица В называется обратной матрицей по отношению к данной матрице А, если
А×В = В×А = Е,
где Е - единичная матрица. В дальнейшем матрицу В будем обозначать А-1.
Таким образом, А×А-1 = А-1×А = Е.
Понятие обратной матрицы дает простое решение системы уравнений, записанное в матричной форме
А×Х = В и Y×А = B
А ¹ 0, следовательно, Х = А-1×В и Y = B×A-1,
где, например,
 ,
,
 ,
,

 .
.
Тогда получаем, что для решения системы необходимо определить А-1.
 .
.
Для определения обратной матрицы напомним некоторые положения из теории:
Определение. Матрица называется регулярной, если ее определитель отличен от нуля.
Теорема. Все регулярные матрицы имеют обратную матрицу.
Д о к а з а т е л ь с т в о :
Пусть

и ![]() (в
этом случае матрица называется невырожденной). Построим для матрицы А
матрицу А*, составив ее из алгебраических дополнений к элементам
матрицы А. Транспонируя ее, имеем
(в
этом случае матрица называется невырожденной). Построим для матрицы А
матрицу А*, составив ее из алгебраических дополнений к элементам
матрицы А. Транспонируя ее, имеем

Это так называемая присоединенная или взаимная матрица.
Разделим все элементы матрицы А на D:

Докажем, что ![]() .
.
Действительно,
![]()
и
![]() ,
,
где
![]() .
.
В силу свойств имеем:
1. Сумма произведений элементов какой-либо строки или столбца определителя на их алгебраические дополнения равна нулю или D.
2. Сумма произведений элементов какой-либо строки или столбца определителя на алгебраические дополнения соответствующих элементов других строк или столбцов равна нулю.
Тогда

Тогда по определению
![]() .
.
Аналогично доказывается
![]() .
.
Окончательно
![]() .
.
З а м е ч а н и я.
1. Если для матрицы А существует А-1, то она единственная.
З а д а ч а 3. Решить систему матричным методом (метод обратной матрицы).

Р е ш е н и е.
Проверим: будет ли матрица  регулярной?
регулярной?

Согласно теореме все регулярные матрицы имеют обратную матрицу. Построим для матрицы А матрицу А*, составив ее из алгебраических дополнений к элементам матрицы А.
 .
.
Тогда

Теперь определим решение системы:
 .
.
О т в е т. х1 = 1, х2 = -2, х3 = 3.
Теория систем линейных уравнений и методы нахождения решений используется в векторной алгебре. Пусть дан еще вектор b(b1, b2, ..., bn). В силу определения равенства векторов и действий между ними мы можем записать
![]() .
(13)
.
(13)
Это равенство можно записать в виде системы n линейных уравнений с k переменными
 .
(14)
.
(14)
Компоненты вектора аj образуют столбец коэффициентов при переменной хj в этой системе, а компоненты вектора b - столбец свободных членов. Верно и обратное: если в произвольно заданной системе линейных уравнений (14) совокупности коэффициентов при одной и той же переменной и свободные члены интерпретировать как соответствующие k векторы , то мы придем к векторному уравнению (13).
Уравнение (13) называется векторной формой записи системы линейных уравнений (14).
Если система (14) несовместна, то разложение вектора b по векторам а1,а2,...,аk невозможно. Если система (14) совместна, то разложение (13) возможно, а каждое решение системы (14) является совокупностью коэффициентов этого разложения.
Уравнение
![]() (15)
(15)
есть векторная запись однородной системы линейных уравнений
 (16)
(16)
Система (16) всегда совместна, так как имеет нулевое решение; и если это решение единственное, то равенство (15) имеет место только при нулевых значениях коэффициентов, то есть система векторов а1, а2, ..., аk линейно независима.
С другой стороны, нулевое решение системы (16) будет единственным тогда и только тогда, когда ее ранг равен числу переменных (r = k), или иначе говоря, утверждение “система векторов а1, а2, ..., аk линейно независима” эквивалентно условию по отношению к рангу матрицы
 ,
(17)
,
(17)
столбцы, которой образованы компонентами этих векторов: ранг этой матрицы должен быть равен числу ее столбцов. Но r £ n, следовательно, если система k векторов линейно независима, то k = r £ n.
Некоторые сведения из теории:
Теорема 1. В пространстве Rn система линейно независимых векторов не может содержать более n векторов.
Теорема 2. Любые n векторов, для которых определитель со столбцами, образованными компонентами векторов, не равен 0, будут линейно независимы.
Таким образом, если
 ,
,
то векторы будут линейно независимыми (k = n, D ¹ 0, система (16) имеет единственное нулевое решение; матрица (17) - квадратная, и ранг матрицы r равен n).
Отсюда следует, что размерность линейного пространства равна n.
Векторы, для
которых D
¹ 0, образуют базис этого пространства.
Решение системы (16) является совокупностью координат вектора ![]() в
этом базисе (в системе (16) в этом случае k = n, а системы (14) и (16) имеют
один и тот же D).
в
этом базисе (в системе (16) в этом случае k = n, а системы (14) и (16) имеют
один и тот же D).
З а д а ч а 4. Даны векторы
а1 (2, 4, 3, 2);
а2 (4, 2, 2, 8);
а3 (4, 5, 8, 7);
а4 (6, 7, 5, 3);
b (18, 24, 13, 6).
Показать, что векторы а1, а2, а3, а4 образуют базис в R4 (линейное 4-х мерное пространство) и определить координаты вектора b в этом пространстве.
Р е ш е н и е.
 .
.
Так как D ¹ 0, следовательно, векторы а1, а2, а3, а4 образуют базис в R4.
Для вычисления координат вектора b в этом базисе составим систему линейных уравнений

Решение этой системы
х1 = 2, х2 = 0, х3 = -1, х4 = 3
представляет собой совокупность координат вектора b в базисе а1, а2, а3, а4, то есть b(2, 0, -1, 3) или
b = 2×a1-a3 + 3×a4.
З а м е ч а н и е.
Базис в R4, как и в любом другом пространстве, может быть выбран не единственным образом.
Пример.
Векторы еj (j = 1, 2, ..., n) образуют базис, если
е1 (1,0,...,0)
е2 (0,1,...,0)
...................
еn (0,0,...,1)
Проверить самостоятельно, что это базис.
Тогда
b = b1×e1 + b2×e2 + ... + bn×en.
В данном случае координаты вектора являются и его компонентами.
III. Ход выполнения лабораторной работы
З а д а н и е. 1. Решить системы линейных уравнений:
а) методом Крамера;
б) матричным методом;
в) методом Гаусса.
2. Проверить, что векторы а1, а2, а3 образуют базис в R3, найти координаты вектора b в этом базисе.
