§1. Основные понятия
Пусть D — некоторое множество чисел. Если задан закон, по которому каждому числу x из множества D ставится в соответствие единственное определенное число y, то будем говорить, что на множестве D задана функция, которую назовём f. Число y — это значение функции f в точке x, что обозначается формулой y = f(x).
Число x называется аргументом функции, множество D — областью определения функции, а все значения y образуют множество E, которое называется множеством значений или областью изменения функции.
Функция f называется возрастающей (убывающей) на множестве G, если для любых чисел х1 и х2 из множества G, таких что x1 < x2, выполняется условие f(x1) < f(x2) (f(x1) > f(x2)).
Так как между множеством действительных чисел и множеством точек числовой оси можно установить взаимно-однозначное соответствие, в дальнейшем изложении понятиям “число х” и “точка х числовой оси” в некоторых случаях будет придаваться один и тот же смысл. Например, вместо “значение функции при значении аргумента, равном х1” будет говориться “значение функции в точке х1”. В нижеследующем определении можно везде заменить выражение “точка х” на выражение “число х”.
Пусть
e
— некоторое положительное число. e-окрестностью
точки x0 называется множество всех точек x,
принадлежащих промежутку (x0 ‑ e, x0 + e),
кроме самой точки x0. Принадлежность точки x
e‑окрестности
точки ![]() можно
выразить с помощью двойного неравенства
можно
выразить с помощью двойного неравенства
0 < êx – x0ç < e.
Число e называется радиусом окрестности.
Рассмотрим функцию y = x2 в точке x0 = 2. Значение функции в этой точке равно 4.
Отметим одну особенность поведения функции в этой точке. Можно
|
|
выбрать какое-либо положительное число e и построить e-окрестность точки y0 = 4. Очевидно, что найдется такая окрестность точки x0 = 2 (на рисунке 1 эта окрестность имеет радиус d) , что если x будет лежать в этой окрестности, то соответствующее значение y, равное x2, попадет в e-окрестность точки y0 = 4. Это заключение справедливо для любого, сколь угодно малого числа e. Здесь точка x0 = 2 выбрана произвольно. Можно было бы для данной функции выбрать любую другую точку и сделать подобное заключение.
Рассмотрим
функцию 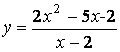 .
Эта функция не определена в точке x0 = 2. При x0 ¹ 2
её можно преобразовать:
.
Эта функция не определена в точке x0 = 2. При x0 ¹ 2
её можно преобразовать:
![]() .
.
|
|
График функции представлен на рисунке 2. Хотя исходная функция не определена в точке x0 = 2 и естественно не равна 3 в этой точке, точка y0 = 3 имеет характерную особенность. Выбрав положительное число e, можно утверждать, что если рассматривать значения x, расположенные достаточно близко к точке x0 = 2 (или лежащие в некоторой окрестности точки x0 = 2, причем радиус этой окрестности зависит от e), то соответствующие значения y попадут в e-окрестность точки y0 = 3. Всё сказанное остаётся справедливым независимо от того, насколько малым выбрано положительное число e.
Введем понятие предела функции. Число A называется пределом функции y = f(x) в точке x0 (иногда говорят, при x, стремящемся к x0), если для любого положительного числа e можно найти такое положительное число d, что для всех x из d-окрестности точки x0 соответствующие значения y попадают в e-окрестность точки y = A.
Можно сформулировать определение предела функции по-другому. Число A называется пределом функции y = f(x) в точке x0, если для любого положительного числа e можно найти такое положительное число d, что для всех x, удовлетворяющих условию
0 < êx – x0ê < d,
выполняется условие
êy – Aê < e.
Тот факт, что A есть предел функции y = f(x) в точке x = x0, записывается формулой
|
|
![]() .
.
Как видно из второго из рассмотренных выше примеров, для того, чтобы функция имела предел в точке x = x0, не требуется, чтобы она была определена в этой точке.
Рассмотрим
функцию 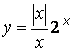 .
Очевидно, что если x > 0, то y = 2x; если x < 0,
то y = –2x; при x = 0 функция не определена.
.
Очевидно, что если x > 0, то y = 2x; если x < 0,
то y = –2x; при x = 0 функция не определена.
График функции изображен на рисунке 3. Легко убедиться в том, что, согласно приведенному выше определению предела, эта функция в точке x = 0 предела не имеет.
Функция y = f(x)
называется непрерывной в точке x = x0, если она
определена в этой точке и ее значение f(x0) равно
пределу функции в этой точке: ![]() .
.
Функция y = x2
непрерывна в точке x = 2, как и во всех точках числовой оси.
Функция 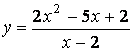 не
является непрерывной в точке x = 2. Функция
не
является непрерывной в точке x = 2. Функция
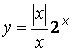 не
является непрерывной в точке x = 0.
не
является непрерывной в точке x = 0.
![]() Функция,
непрерывная в каждой точке открытого промежутка, называется непрерывной на
этом промежутке.
Функция,
непрерывная в каждой точке открытого промежутка, называется непрерывной на
этом промежутке.
Приведем свойства предела функции.
1. Функция не может иметь в одной точке два разных предела.
2.
![]() ,
если C — постоянная функция.
,
если C — постоянная функция.
3. Если существует![]() и
C — постоянная функция, то
и
C — постоянная функция, то
![]() .
.
4. Если существуют![]() и
и
![]() ,
то существует
,
то существует ![]() ,
равный
,
равный ![]() ,
а также существует
,
а также существует ![]() ,
равный
,
равный ![]() .
Если при этом
.
Если при этом ![]() ,
то существует
,
то существует![]() ,
равный
,
равный ![]() .
.
Введем определения так называемых “односторонних пределов”.
Число B
называется пределом функции f(x) в точке a
справа (это записывается в виде формулы
![]() ),
если для любого положительного числа e
найдется положительное число d,
такое что из из условия 0 < x – a < d
будет следовать êB –f(x) ê < e.
),
если для любого положительного числа e
найдется положительное число d,
такое что из из условия 0 < x – a < d
будет следовать êB –f(x) ê < e.
Согласно
приведенному определению ![]() .
Отметим, что обыкновенного предела функция
.
Отметим, что обыкновенного предела функция
![]() в
точке x = 0 не имеет.
в
точке x = 0 не имеет.
Число С
называется пределом функции f(x) в точке b
слева (это записывается в виде формулы
![]() ),
если для любого положительного числа e
найдется положительное число d
такое, что из условия 0 < b – x < d
будет следовать êC – f(x)ê < e.
),
если для любого положительного числа e
найдется положительное число d
такое, что из условия 0 < b – x < d
будет следовать êC – f(x)ê < e.
Очевидно, что
функция 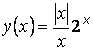 (её
график, изображен на рисунке 3) имеет два односторонних предела в точке x = 0:
(её
график, изображен на рисунке 3) имеет два односторонних предела в точке x = 0:
![]() ;
;
![]() .
.
Функция f(x) называется непрерывной в точке a справа (непрерывной в точке b слева), если
![]() (
(![]() ).
).
Функция
![]() непрерывна
справа в точке x=0.
непрерывна
справа в точке x=0.
Функция называется непрерывной на замкнутом промежутке [a, b], если она непрерывна на открытом промежутке (a, b), непрерывна справа в точке a и непрерывна слева в точке b.
Достаточно просто можно доказать теорему, связывающую понятия предела функции в точке и односторонних пределов. Мы ограничимся только формулировкой теоремы.
Для того,
чтобы выполнялось равенство
![]() ,
необходимо и достаточно, чтобы одновременно выполнялись два равенства:
,
необходимо и достаточно, чтобы одновременно выполнялись два равенства:
![]() ;
;
![]()
В дальнейшем нам понадобятся понятия предела функции в бесконечно удалённых точках. Рассмотрим сначала функцию f(x), определенную на полубесконечном промежутке (х0; ¥). Число А называется пределом функции f(x) при х, стремящемся к бесконечности:
![]() ,
,
если для любого положительного числа e можно найти такое положительное число M (зависящее от e), что для всех чисел х, превосходящих М, выполняется условие:
½f(x) – A½ < e.
Пусть теперь
функция f(x)
определена на полубесконечном промежутке
(–¥;
х0).
Число А называется пределом функции
f(x)
при
х, стремящемся к минус бесконечности:
![]() ,
,
если для любого положительного числа e можно найти такое положительное число M (зависящее от e), что для всех чисел х, меньших, чем – М, выполняется условие:
½f(x) – A½ < e.
Отметим два, так называемых, "замечательных предела".
1. ![]() .
Геометрический смысл этой формулы заключается в том, что прямая
.
Геометрический смысл этой формулы заключается в том, что прямая
![]() является
касательной к графику функции
является
касательной к графику функции ![]() в
точке
в
точке ![]() .
.
2. ![]() .
Здесь e — иррациональное число, приблизительно равное 2,72.
.
Здесь e — иррациональное число, приблизительно равное 2,72.
Приведем пример применения понятия предела функции в экономических расчетах. Рассмотрим обыкновенную финансовую сделку: предоставление в долг суммы S0 с условием, что через период времени T будет возвращена сумма ST. Определим величину r относительного роста формулой
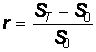 .
(1)
.
(1)
Относительный рост можно выразить в процентах, умножив полученное значение r на 100.
Из формулы (1) легко определить величину ST:
ST = S0(1 + r)
При расчете по долгосрочным кредитам, охватывающим несколько полных лет, используют схему сложных процентов. Она состоит в том, что если за 1-й год сумма S0 возрастает в (1 + r) раз, то за второй год в (1 + r) раз возрастает сумма S1 = S0(1 + r), то есть S2 = S0(1 + r)2. Аналогично получается S3 = S0(1 + r)3. Из приведенных примеров можно вывести общую формулу для вычисления роста суммы за n лет при расчете по схеме сложных процентов:
Sn = S0(1 + r)n.
В финансовых
расчетах применяются схемы, где начисление сложных процентов производится
несколько раз в году. При этом оговариваются годовая ставка r и
количество начислений за год k. Как правило, начисления производятся
через равные промежутки времени, то есть длина каждого промежутка Tk
составляет ![]() часть
года. Тогда для срока в T лет (здесь T не обязательно является
целым числом) сумма ST рассчитывается по формуле
часть
года. Тогда для срока в T лет (здесь T не обязательно является
целым числом) сумма ST рассчитывается по формуле
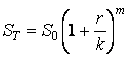 (2)
(2)
Здесь
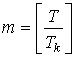 —
целая часть числа
—
целая часть числа ![]() ,
которая совпадает с самим числом, если, например, T ‑ целое число.
,
которая совпадает с самим числом, если, например, T ‑ целое число.
Пусть годовая ставка равна r и производится n начислений в год через равные промежутки времени. Тогда за год сумма S0 наращивается до величины, определяемой формулой
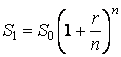 (3)
(3)
В теоретическом анализе и в практике финансовой деятельности часто встречается понятие “непрерывно начисляемый процент”. Чтобы перейти к непрерывно начисляемому проценту, нужно в формулах (2) и (3) неограниченно увеличивать соответственно, числа k и n (то есть устремить k и n к бесконечности) и вычислить, к какому пределу будут стремиться функции ST и S1. Применим эту процедуру к формуле (3):
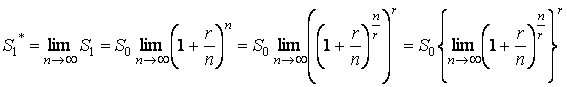 .
.
Заметим, что предел в фигурных скобках совпадает со вторым замечательным пределом. Отсюда следует, что при годовой ставке r при непрерывно начисляемом проценте сумма S0 за 1 год наращивается до величины S1*, которая определяется из формулы
S1* = S0er. (4)
Пусть теперь сумма S0 предоставляется в долг с начислением процента n раз в год через равные промежутки времени. Обозначим re годовую ставку, при которой в конце года сумма S0 наращивается до величины S1* из формулы (4). В этом случае будем говорить, что re — это годовая ставка при начислении процента n раз в год, эквивалентная годовому проценту r при непрерывном начислении. Из формулы (3) получаем
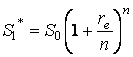 .
.
Приравнивая правые части последней формулы и формулы (4), полагая в последней T = 1, можно вывести соотношения между величинами r и re:
 ,
,
 .
.
Эти формулы широко используются в финансовых расчётах.