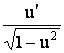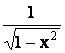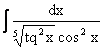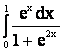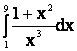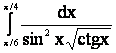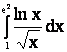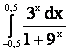МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНЕЦКИЙ
НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
ВЫСШАЯ
МАТЕМАТИКА
Донецк 2000
ВЫСШАЯ МАТЕМАТИКА
Методические указания и контрольные задания
(для студентов экономических
специальностей заочной формы обучения)
У т в е р ж д е н о
на заседании
кафедры математики и
математических
методов в экономике
Протокол
№ 3 от 25.10.99
ББК 22.1
УДК 516+517(076.1)
Высшая математика.
Методические указания и контрольные задания / Сост. Н.Е. Зима, М.И. Медведева, Миронова Е.М. и др. - Донецк: ДонНУ, 2000.-77с.
Составлены в соответствии с программой
курса “Математика для экономистов” высших учебных заведений (для студентов
экономических специальностей заочной формы обучения).
Составители:
Н.Е. Зима, доц.
М.И. Медведева, ст преп.
Е.М. Миронова, ассист.
Е.Г. Новожилова,
ст.преп.
Г.М. Николайчук, ст.преп.
А.В. Онюшкина, ассист.
Ответственный
за выпуск:
В.
В. Христиановский, проф., зав. кафедрой МММЭ
Методика изучения математики
Основной формой обучения студента-заочника
является самостоятельная работа над учебным материалом по математическим
курсам. Такая работа включает в себя: чтение учебников, решение задач,
выполнения контрольных работ. В помощь студентам организуются чтение лекций и
практические занятия.
Завершающий
этап изучения курса высшей математики – защита контрольной работы и сдача
экзаменов в соответствии с учебным планом.
Студент
выполняет контрольную работу, вариант которой задается с помощью приведенной
ниже таблицы. Для определения номера соответствующего задания необходимо
выписать фамилию, имя, отчество и найти номер соответствующего задания в
таблице:
|
|
Номер задания |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
А |
1 |
26 |
51 |
76 |
101 |
126 |
151 |
176 |
201 |
|
|
БЬ |
2 |
27 |
52 |
77 |
102 |
127 |
152 |
177 |
202 |
|
|
В |
3 |
28 |
53 |
78 |
103 |
128 |
153 |
178 |
203 |
|
|
ГЫ |
4 |
29 |
54 |
79 |
104 |
129 |
154 |
179 |
204 |
|
|
Д |
5 |
30 |
55 |
80 |
105 |
130 |
155 |
180 |
205 |
|
|
ЗЧ |
6 |
31 |
56 |
81 |
106 |
131 |
156 |
181 |
206 |
|
|
ИЭ |
7 |
32 |
57 |
82 |
107 |
132 |
157 |
182 |
207 |
|
|
КЪ |
8 |
33 |
58 |
83 |
108 |
133 |
158 |
183 |
208 |
|
|
ЛЦ |
9 |
34 |
59 |
84 |
109 |
134 |
159 |
184 |
209 |
|
|
М |
10 |
35 |
60 |
85 |
110 |
135 |
160 |
185 |
210 |
|
|
Н |
11 |
36 |
61 |
86 |
111 |
136 |
161 |
186 |
211 |
|
|
О |
12 |
37 |
62 |
87 |
112 |
137 |
162 |
187 |
212 |
|
|
П |
13 |
38 |
63 |
88 |
113 |
138 |
163 |
188 |
213 |
|
|
С |
14 |
39 |
64 |
89 |
114 |
139 |
164 |
189 |
214 |
|
|
ТЙ |
15 |
40 |
65 |
90 |
115 |
140 |
165 |
190 |
215 |
|
|
У |
16 |
41 |
66 |
91 |
1216 |
141 |
166 |
191 |
216 |
|
|
Ш |
17 |
42 |
67 |
92 |
117 |
142 |
167 |
192 |
217 |
|
|
Ф |
18 |
43 |
68 |
93 |
118 |
143 |
168 |
193 |
218 |
|
|
Ж |
19 |
44 |
69 |
94 |
119 |
144 |
169 |
194 |
219 |
|
|
Е |
20 |
45 |
70 |
95 |
120 |
145 |
170 |
195 |
220 |
|
|
Я |
21 |
46 |
71 |
96 |
121 |
146 |
171 |
196 |
221 |
|
|
Щ |
22 |
47 |
72 |
97 |
122 |
147 |
172 |
197 |
222 |
|
|
Ю |
23 |
48 |
73 |
98 |
123 |
148 |
173 |
198 |
223 |
|
|
Р |
24 |
49 |
74 |
99 |
124 |
149 |
174 |
199 |
224 |
|
|
Х |
25 |
50 |
75 |
100 |
125 |
150 |
175 |
200 |
225 |
|
1.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
1.1.
Векторная алгебра
Вектором называется упорядоченный набор из 3-х чисел (геометрическая
интерпретация- направленный отрезок ) и обозначается ![]() (или
(или ![]() ), где точка А рассматривается как начало, а точка В – как
конец вектора.
), где точка А рассматривается как начало, а точка В – как
конец вектора.
Пусть даны ось l и вектор ![]() =
= ![]() . Обозначим через A¢ и B¢ соответственно проекции
точек A и B на ось l.
. Обозначим через A¢ и B¢ соответственно проекции
точек A и B на ось l.
В
![]()
![]()
![]()
А
А¢ В¢ l

Проекцией вектора ![]() на ось l (обозначение прl
на ось l (обозначение прl![]() ) называется число, равное длине вектора
) называется число, равное длине вектора ![]() , взятой со знаком плюс, если направление вектора
, взятой со знаком плюс, если направление вектора ![]() совпадает с
направлением оси l, и со знаком минус – в
противном случае. Аналогично определяется проекция вектора на вектор.
совпадает с
направлением оси l, и со знаком минус – в
противном случае. Аналогично определяется проекция вектора на вектор.
Свойства проекции вектора на ось
1. прl ![]() = ê
= ê![]() êcosj, где j - угол между вектором
êcosj, где j - угол между вектором ![]() и осью l;
и осью l;
2. прl (![]() +
+ ![]() ) = прl
) = прl ![]() + прl
+ прl ![]() ;
;
3. прl (k![]() ) = k прl
) = k прl ![]() .
.
Пример. Пусть ![]() ,
, ![]() и
и ![]() - векторы,
составляющие с осью l
соответственно углы
- векторы,
составляющие с осью l
соответственно углы ![]() и
и ![]() , причем ê
, причем ê![]() ê= 1, ê
ê= 1, ê![]() ê= 2, ê
ê= 2, ê![]() ê= 3. Найти проекцию вектора
3
ê= 3. Найти проекцию вектора
3![]() -
- ![]() + 5
+ 5![]() на ось l.
на ось l.
Решение. По свойству 1 проекций имеем
прl ![]() = ê
= ê![]() êcos
êcos![]() =
= ![]() , прl
, прl ![]() = ½b1êcosp = 2(-1) = -2,
= ½b1êcosp = 2(-1) = -2,
прl![]() = ê
= ê![]() êcos
êcos![]() = 3
= 3![]() =
= ![]() .
.
Согласно свойствам 2 и 3 проекций находим
прl (3![]() -
- ![]() + 5
+ 5![]() ) = 3прl
) = 3прl ![]() - прl
- прl ![]() + 5 прl
+ 5 прl ![]() =
= ![]() + 2 -
+ 2 - ![]() = -4.
= -4.
Разложение вектора по координатным осям
Оx, Оy и Оz записывается в виде ![]() = x
= x![]() + y
+ y![]() + z
+ z![]() или
или ![]() = (x, y, z), где x, y, z -
проекции
= (x, y, z), где x, y, z -
проекции ![]() на оси Оx, Оy, Оz;
на оси Оx, Оy, Оz; ![]() ,
, ![]() ,
, ![]() - единичные векторы
(орты), совпадающие по направлению с этими осями. Проекции x, y, z
называются координатами вектора.
- единичные векторы
(орты), совпадающие по направлению с этими осями. Проекции x, y, z
называются координатами вектора.
Длина
вектора ![]() = (x, y, z), вычисляется по формуле
= (x, y, z), вычисляется по формуле
![]() .
.
Если a, b, g - углы между вектором ![]() = (x, y, z) и осями Оx, Оy, Оz , то cosa, cosb, cosg называется направляющими косинусами вектора
= (x, y, z) и осями Оx, Оy, Оz , то cosa, cosb, cosg называется направляющими косинусами вектора ![]() и вычисляется по
формулам
и вычисляется по
формулам
![]() .
.
Если
известны координаты точек A(x1, y1, z1) и B(x2, y2, z2), то
![]() = (x2 - x1, y2 - y1, z2 - z1).
= (x2 - x1, y2 - y1, z2 - z1).
Расстояние между двумя точками A(x1, y1, z1) и B(x2, y2, z2) вычисляется по формуле
![]() .
.
Скалярным произведением двух векторов ![]() и
и ![]() называется число,
равное произведению длин этих векторов на косинус угла j между ними
называется число,
равное произведению длин этих векторов на косинус угла j между ними
![]() ×
× ![]() = |
= |![]() ||
||![]() |cosj.
|cosj.
Свойства скалярного
произведения
1. ![]() ×
× ![]() =
= ![]() ×
× ![]() ;
;
2. ![]() × (
× (![]() +
+ ![]() ) =
) = ![]() ×
×![]() +
+![]() ×
×![]() ;
;
3.
(l![]() )×
)×![]() = (l
= (l![]() )
)![]() = l(
= l(![]() ×
×![]() ) (сочетание значений по отношению к скалярному произведению);
) (сочетание значений по отношению к скалярному произведению);
4. ![]() ×
×![]() = 0, если
= 0, если ![]() = 0, либо
= 0, либо ![]() = 0, либо
= 0, либо ![]() ^
^ ![]() ;
;
5.
![]() ×
×![]() = |
= |![]() |2 или
|2 или ![]() 2 = |
2 = |![]() |2 (скалярный квадрат вектора
равен квадрату его длины).
|2 (скалярный квадрат вектора
равен квадрату его длины).
Пусть векторы ![]() (x1, y1, z1) и
(x1, y1, z1) и ![]() ( x2, y2, z2) заданы своими
координатами.
( x2, y2, z2) заданы своими
координатами.
Тогда скалярное произведение
этих векторов находится по формуле
![]() ×
×![]() = x1 x2 + y1 y2 + z1 z2,
= x1 x2 + y1 y2 + z1 z2,
а косинус угла между ними –
по формуле

Пример. Векторы ![]() и
и ![]() образуют угол
образуют угол ![]() . Найти длину вектора
. Найти длину вектора ![]() = 2
= 2![]() - 3
- 3![]() , если |
, если |![]() | = 2, |
| = 2, |![]() | = 1.
| = 1.
Решение. Согласно свойству 5 скалярного произведения,
квадрат длины вектора ![]() равен его скалярному
квадрату. Найдем скалярный квадрат
равен его скалярному
квадрату. Найдем скалярный квадрат ![]()
|![]() |2 = (2
|2 = (2![]() - 3
- 3![]() )2 = 4
)2 = 4![]() 2 - 12
2 - 12![]() ×
×![]() + 9
+ 9![]() 2 = 4|
2 = 4|![]() |2 - 12|
|2 - 12|![]() ||
||![]() |cosj + 9|
|cosj + 9|![]() |2 =
|2 =
= 4×22 - 12×2×1×cos![]() + 9×12 = 16 - 12 + 9
= 13,
+ 9×12 = 16 - 12 + 9
= 13,
следовательно, |![]() | =
| = ![]() .
.
Пример. Найти внутренний угол ![]() в треугольнике с
вершинами A(1, 2, -1); B(5, 5,
11); C(13, 18, 20).
в треугольнике с
вершинами A(1, 2, -1); B(5, 5,
11); C(13, 18, 20).
Решение: Искомый угол – это угол между векторами ![]() =
= ![]() =(4; 3; 12) и
=(4; 3; 12) и ![]() =
= ![]() = (12; 16; 21). По
формуле
= (12; 16; 21). По
формуле 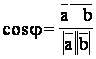 имеем
имеем
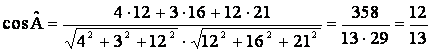 ,
,
таким образом, ![]() .
.
1.2. Прямая линия на плоскости
Если точка M(x; y; z) делит
отрезок между точками A(x1, y1, z1) и B(x2, y2, z2) в отношении l (т.е. |АМ|:|МВ| = l), то ее координаты находят по формулам
![]()
В частности, при делении отрезка пополам, т.е. при l = 1, получаем формулы для вычисления
координат середины отрезка
![]()
Уравнением линии на плоскости Oxy называется уравнение,
которому удовлетворяют координаты (x, y) каждой точки данной линии
и не удовлетворяют координаты любой точки, не лежащей на этой линии. Всякое
уравнение первой степени относительно текущих координат x и y, т.е.
уравнение вида
Ax + By + C = 0,
где A, B, C - постоянные коэффициенты, причем A2 + B2 ¹ 0 определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.
Пример. Построить прямую 3x – 2y +6 = 0.
х у 3 2 1
В
А
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Решение: Для построения прямой достаточно
знать какие-либо две ее точки, например, точки пересечения с осями координат.
Точку A пересечения прямой с осью Оx можно
получить, если в уравнении прямой принять y = 0. Тогда имеем 3x + 6 =
0, т.е. x = -2. Таким образом, A(-2, 0). Аналогично, точка B -
точка пересечения прямой с осью Оy, имеет координату x = 0.
Следовательно, ордината точки B находится из уравнения –2y + 6 =
0, т.е. y = 3. Значит, B(0, 3).
Решение: Для построения прямой достаточно
знать какие-либо две ее точки, например, точки пересечения с осями координат.
Точку A пересечения прямой с осью Оx можно
получить, если в уравнении прямой принять y = 0. Тогда имеем 3x + 6 =
0, т.е. x = -2. Таким образом, A(-2, 0). Аналогично, точка B -
точка пересечения прямой с осью Оy, имеет координату x = 0.
Следовательно, ордината точки B находится из уравнения –2y + 6 =
0, т.е. y = 3. Значит, B(0, 3).
![]()
-2 -1 1 2
Если в общем уравнении прямой B ¹ 0, то разрешив его
относительно y, получаем уравнение вида
y = kx + b
(здесь k = - A/B, b = -C/B). Его называют уравнением с угловым коэффициентом, т.к. k = tga, где a - угол, образованный прямой с положительным направлением оси Ох. Угловой коэффициент k прямой, заданной двумя точками A(xA, yA) и B(xB, yB), где xA ¹ xB, можно вычислить по формуле
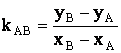 .
.
Уравнение прямой, проходящей через заданную
точку A(xA, yA), с угловым коэффициентом k, записывается
в виде
y – yA = k(x - xA).
Рассмотрим
две прямые (не параллельные оси Оy), заданные уравнениями с
угловыми коэффициентами l1: y = k1x + b1, и l2: y = k2x + b2. Пусть j- угол между этими прямыми,
тогда
 .
.
Условия
пересечения, параллельности, перпендикулярности
или совпадения двух прямых,
заданных общими уравнениями A1x + B1y +C1 = 0
и A2x + B2y +C2 = 0 имеют вид
1)
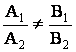 (пересечение);
(пересечение);
2)
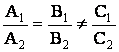 (параллельность);
(параллельность);
3)
А1А2 + В1В2 = 0 (перпендикулярность);
4)
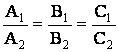 (совпадение).
(совпадение).
Если известны угловые
коэффициенты k1 и k2 прямых, то условия параллельности и перпендикулярности
этих прямых имеют вид
k1 = k2 и k1 = -1/k2
соответственно.
Уравнение прямой, проходящей через две
данные точки А(хА,уА) и В(хВ,уВ),
имеет вид
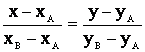 .
.
Если прямая проходит через точки А и В и параллельна
оси Ох, т.е. уА = уВ (или оси Оу, т.е. хА = хВ),
то уравнение такой прямой задается формулой у = уВ (х = хВ, соответственно).
Расстояние от точки М(х0, у0) до прямой Ах + Ву + С = 0 находится по
формуле
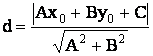 .
.
Пример. Даны вершины треугольника
А(2; -2), В(-4; 1), С(-1; 2). Сделать чертеж и найти:
1) периметр треугольника;
2) уравнение высоты, проведенной
через вершину С;
3) уравнение прямой ЕС,
проходящей через точку С и параллельной прямой АВ;
4) уравнение медианы СМ,
проведенной через вершину С;
5) угол, который медиана ВМ1,
проведенная через вершину В, образует со стороной ВС;
6) координаты точки К -
пересечения медиан треугольника;
7) площадь треугольника АВС;
8) систему линейных неравенств,
определяющих треугольник АВС.
Решение. 1) Периметр треугольника РАВС равен |AB| + |BC| + |CA|. Длины
сторон найдем по формуле расстояния между двумя точками. Имеем
![]() ,
,
![]() ,
,
![]() .
.
Тогда PABC ![]() » 14,87.
» 14,87.
2) Найдем уравнение высоты CD. Так как CD ^ АВ, то по условию перпендикулярности двух прямых kCD = -1/kAB. Вычислим угловой коэффициент прямой AB
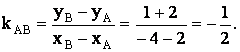
Таким образом,. kCD = 2. Подставив координаты точки C(-1; 2) и угловой коэффициент kCD = 2 в формулу уравнения прямой с угловым коэффициентом, получим уравнение прямой CD
у – 2 = (2х - 2) или 2х – у + 4 = 0.
3. Так как прямые АВ и ЕС параллельны, по
условию параллельности двух прямых kАВ = kЕС.
Тогда ![]() и уравнение прямой ЕС
принимает вид: у - 2 = -1/2(х + 1) или 2у – 4 = - (х + 1) и, окончательно, х +
2у – 3 = 0.
и уравнение прямой ЕС
принимает вид: у - 2 = -1/2(х + 1) или 2у – 4 = - (х + 1) и, окончательно, х +
2у – 3 = 0.
4) Найдем координаты точки М. Так как СМ - медиана, то точка М является серединой отрезка АВ и
![]()
![]()
Так как хМ = хС, то уравнение СМ имеет вид: х = -1.
5) Найдем угол a между прямыми ВМ1 и ВС, используя формулу тангенса угла между двумя прямыми. Предварительно вычислим угловые коэффициенты прямых ВМ1 и ВС. Точка М1 является серединой отрезка АС и, следовательно, как и в предыдущем случае ее координаты
![]() ,
, ![]() ,
,
т.е. М1(1/2;0). Тогда,
 ,
,
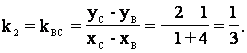
и
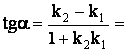

т.е. ![]() .
.
6) Для определения координат точки пересечения медиан треугольника, достаточно знать уравнения двух его медиан. Выше было найдено, что уравнение медианы СМ. Найдем уравнение медианы ВМ1, используя формулу уравнения прямой, проходящей через две заданные точки. Получаем
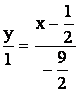 или
или ![]() ;
;
После преобразования получаем уравнение медианы BM1 в общем виде 2x + 9y – 1 = 0. Точка К лежит и на прямой СМ и на прямой ВМ1. Следовательно, координаты удовлетворяют уравнениям обеих прямых. Значит, для вычисления координат точки К достаточно решить систему уравнений, содержащую уравнения первой и второй прямых.
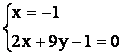 ~
~ 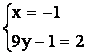 ~
~ 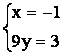 ~
~ 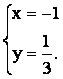
Итак, точка
пересечения медиан треугольника ![]() .
.
![]()
7) Площадь треугольника может
быть вычислена по формуле ![]() , где a
= ½AB½ - длина основания, h = ½CD½-
длина высоты треугольника. В нашем примере длина основания треугольник ½AB½ = 3
, где a
= ½AB½ - длина основания, h = ½CD½-
длина высоты треугольника. В нашем примере длина основания треугольник ½AB½ = 3![]() (было вычислено выше, см 1). Длину высоты СД найдем
как расстояние от точки C
до прямой AB. Для этого
определим сначала общее уравнение прямой АВ. Имеем
(было вычислено выше, см 1). Длину высоты СД найдем
как расстояние от точки C
до прямой AB. Для этого
определим сначала общее уравнение прямой АВ. Имеем
![]()
или после преобразований х +2у + 2 = 0. Таким образом, А = 1, В = 2, С = 2. Кроме того, из условия известны координаты точки С: хС =-1, уС = 2. Тогда, по формуле расстояния от точки до прямой, имеем
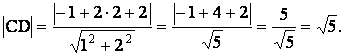
Следовательно, площадь треугольника
![]() .
.
![]()
8) Сделаем чертеж.

Для того, чтобы записать систему неравенств, определяющих треугольник, необходимо знать уравнения всех трех сторон. Найдем уравнения всех сторон треугольника. Уравнение прямой АВ - х +2у + 2 = 0 - было найдено выше (см. 7). Найдем теперь уравнения прямых ВС и АС, используя формулу прямой, проведенной через две заданные точки. Для прямой ВС имеем
![]()
или после преобразований х – 3у + 7 = 0. Для прямой АС аналогично получаем
![]()
или после преобразований 4х + 3у –2 = 0. Теперь определяем систему неравенств. По чертежу видно, что точка с координатами (0, 0) лежит внутри треугольника. Каждая прямая делит плоскость на две полуплоскости. Подставим в каждое уравнений прямой координаты точки (0, 0) и определим вид неравенства. Для прямой АВ, после подстановки координат (0, 0) получаем:
0 + 2×0 + 2 = 2.
Так как 2 ³ 0, то соответствующее неравенство имеет вид
х + 2у + 2 ³ 0.
Подставим в уравнение прямой ВС координаты точки (0, 0)
0 - 3×0 + 7 = 7.
Так как 7 ³ 0, то неравенство имеет вид
х - 3у + 7 ³ 0.
Подставим в уравнение прямой АС координаты точки (0, 0)
4×0 + 3×0 - 2 = - 2.
Так как –2 £ 0, то получаем неравенство
4х +3у –2 £ 0.
Отсюда система линейных неравенств, определяющих треугольник АВС

2. ТЕОРИЯ ПРЕДЕЛОВ
Число А называется пределом
функции f(x) при х ® а (или в точке а), если для
любого наперед заданного положительного числа e найдется такое положительное число d , что
½f(х) - А
½< e
для всех х таких, что½х – а ½ < d.
Обозначают
![]() .
.
2.1 Основные свойства пределов
Если функции f(x) и j(х) при х ® а имеют конечные пределы, причем ![]()
![]() и
и![]()
![]() ,
то имеют место следующие равенства:
,
то имеют место следующие равенства:
1.
![]() .
.
2.
![]() .
.
3.
 , если
, если ![]() .
.
Частое
применение находят следующие пределы:

Примеры.

 .
.
2.2.
Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых
Функция a(х) называется бесконечно малой при х, стремящемся к а, если
![]() .
.
Функция a(х) называется бесконечно большой при х, стремящемся к а, если
![]()
Связь между
бесконечно малой и бесконечно большой функциями
1. Функция, обратная по величине бесконечно большой, является бесконечно малой.
2. Функция, обратная по
величине бесконечно малой, отличной от нуля, есть бесконечно большая.
Свойства
бесконечно малых и бесконечно больших функций
1. Сумма или разность двух бесконечно малых функций есть функция бесконечно малая.
2. Произведение бесконечно
малой функции на функцию ограниченную есть функция бесконечно малая.
3. Сумма бесконечно большой
функции и функции ограниченной есть бесконечно большая функция.
4. Сумма двух бесконечно больших
функций одинакового знака есть бесконечно большая функция того же знака.
Сравнение
бесконечно малых. Принцип эквивалентности
Бесконечно малые при х ® а функции a(х) и b(х) сравниваются между собой:
1) Если
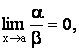
то a есть бесконечно малая высшего порядка, чем b.
2) Если

то a есть бесконечно малая низшего порядка, чем b.
3) Если
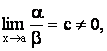
то a есть бесконечно малая того же порядка, чем b.
4) Если
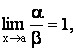
то ![]() a и b
называются эквивалентными бесконечно
малыми. (Обозначают a ~ b.)
a и b
называются эквивалентными бесконечно
малыми. (Обозначают a ~ b.)
5)
Если a
~ b и
существует  то существует
то существует 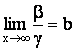 .
.
Пример.
Вычислить предел
![]()
Решение. Используя свойство 5 и эквивалентность arcsinx
~ sinx ~ x при x ® 0, получаем
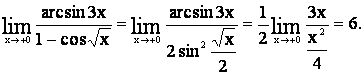
2.3. Примеры вычисления пределов
Предел функции не зависит от того, определена она в предельной точке или нет. Но в практике вычисления пределов элементарных функций это обстоятельство имеет существенное значение.
1. Если функция является элементарной и если предельное значение аргумента принадлежит ее области определения, то вычисление предела функции сводится к простой подстановке предельного значения
Пример.
![]() .
.
2. Если аргумент стремится к ¥ или к числу, которое не
принадлежит области определения функции, то в каждом таком случае нахождения
предела функции требует специального исследования.
Более
сложные случаи нахождения предела функции ![]() рассмотрим далее
каждый в отдельности.
рассмотрим далее
каждый в отдельности.
3. Если при х ® а или х ® ¥ функция f(x)
представляет отношение двух бесконечно больших функций ![]() .
.
Пример.

Чтобы
вычислить такие пределы, числитель и знаменатель дроби нужно разделить на
старшую степень переменной х (в примерах х3 и х соответственно, т.к.
при х ® ¥ величины 1/х3,1/х
являются бесконечно малыми). После чего легко получаем результат.
Замечание. Если в числителе и
знаменателе стоят многочлены одной степени, то предел такой дроби при х ® ¥ равен отношению
коэффициентов при старших степенях.
4. При х ® а или х ® ¥ функция f(x)
представляет отношение двух бесконечно малых функций ![]() . Если необходимо вычислить предел дроби, числитель и
знаменатель которой - многочлены, обращающиеся в нуль в предельной точке х = а,
то оба многочлена нужно разложить на простые множители и сократить на (х - а),
а затем вычислить предел.
. Если необходимо вычислить предел дроби, числитель и
знаменатель которой - многочлены, обращающиеся в нуль в предельной точке х = а,
то оба многочлена нужно разложить на простые множители и сократить на (х - а),
а затем вычислить предел.
Пример.
1) 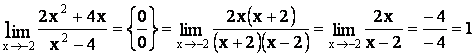 .
.
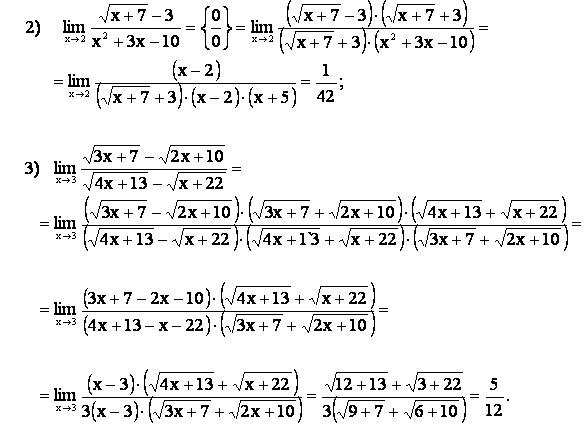
5. Пусть при х ® а или х ® ¥ функция f(x)
представляет собой произведение бесконечно малой функции на бесконечно большую {0×¥}. Этот случай нахождения предела
функции приводится путем преобразования функции к одному из двух
рассматриваемых случаев, а именно к случаю ![]() . Например,
. Например,
f(x)×g(x) = 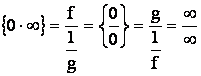 .
.
Пример. Вычислить предел
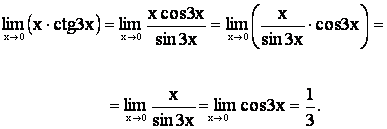
6. Случай, когда при х ® а или х ® ¥ функция f(x)
представляет степень, основание которой стремится к 1, а показатель – к ¥ {1¥}. В этом случае для
нахождения предела функции используется второй замечательный предел.
Пример. Вычислить предел.
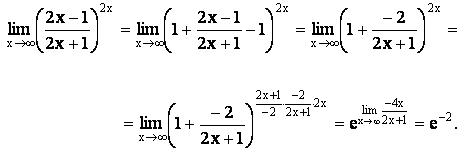
7. Случай, когда при х ® а или х ® ¥ функция f(x)
представляет разность двух положительных бесконечно больших функций {¥ - ¥}.Этот случай нахождения
предела можно привести к случаям 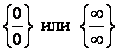 путем преобразования
функции к виду дроби.
путем преобразования
функции к виду дроби.
Пример. Вычислить пределы
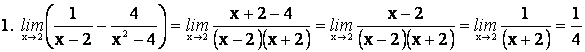
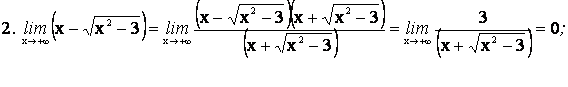
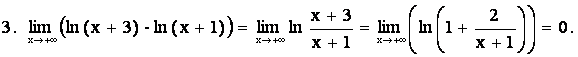
3. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Рассмотрим функцию у = f(x), которая определена на
некотором интервале (а, b) и непрерывна на этом интервале. Производной функции ![]() по независимой
переменной х называется предел, к которому стремится отношение приращения
функции Dу к приращению
аргумента Dх, когда приращение
аргумента стремится к нулю. т.е.
по независимой
переменной х называется предел, к которому стремится отношение приращения
функции Dу к приращению
аргумента Dх, когда приращение
аргумента стремится к нулю. т.е.
![]()
Производная обозначается ![]() или f¢(x), или
или f¢(x), или ![]() .
.
Операция нахождения производной называется дифференцированием. Функция называется
дифференцированной в некоторой точке х, если в этой точке она имеет
определенную производную и при этом функция будет непрерывной.
3.1. Правила
дифференцирования алгебраических функций
1. если с – константа, то![]() ;
;
2. если y = u(х) ± v(х), то y¢ = u¢(х) ± v¢(х);
3. если y = u(х)v(х), то
y¢ = u¢(х)v(х) + u(х)v¢(х);
4.
если 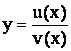 , то
, то 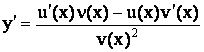 .
.
Пусть у = у(u) и u = u(х) –
дифференцируемые функции. Тогда сложная
функция
у = у[u(x)] есть также
дифференцируемая функция, причем
у¢х=у¢u ×u¢x.
Таблица
производных основных элементарных функций
|
1 |
y =
с, |
y¢ = 0 |
|
|
|
2 |
y =
х, |
y¢= 1 |
|
|
|
3 |
у = xn , |
y¢ = nxn-1 |
у = un |
y¢ = nun-1 u¢ |
|
4 |
|
|
|
|
|
5 |
у = lnx |
y¢ = 1/x |
у = lnu |
y¢ = u¢/u |
|
6 |
у = ax, |
y¢ = axlna |
у = au, |
y¢ = aulna u¢ |
|
7 |
y
= ex, |
y¢ = ex |
y
= eu, |
y¢ = eu u¢ |
|
8 |
у = sinx, |
y¢ = cosx |
у = sinu, |
y¢ = cosu u¢ |
|
9 |
у =
соsх, |
y¢ = -sinx |
у =
соsu, |
y¢ = -sinu u¢ |
|
10 |
y =
tgx, |
|
y = tgu, |
|
|
11 |
у =
ctgx, |
|
у =
ctgu, |
|
|
12 |
у=arcsinx, |
y¢= |
у=arcsinu, |
y¢= |
|
13 |
у=arccosx |
y¢= |
у=arccosu |
y¢= |
|
14 |
у=arctgx, |
y¢= |
у=arctgu, |
y¢= |
|
15 |
у=arcctgx, |
y¢=- |
у=arcctgu, |
y¢=- |
Пример . Продифференцировать функции 1) y = ![]() , 2)
, 2) 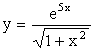 ,
,
3) у = arcsinln(x![]() + 2x + 1).
+ 2x + 1).
Решение: 1) y
= ![]() . Применим правило дифференцирования произведения двух
функций
. Применим правило дифференцирования произведения двух
функций
![]() ;
;
2) Пусть  Применим правило
дифференцирования частного двух фукций и сложной функции.
Применим правило
дифференцирования частного двух фукций и сложной функции.
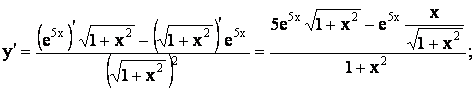
3) Пусть у = arcsinln(x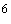 + 2x + 1). Применяя правило дифференцирования сложной
функции и суммы, получим
+ 2x + 1). Применяя правило дифференцирования сложной
функции и суммы, получим
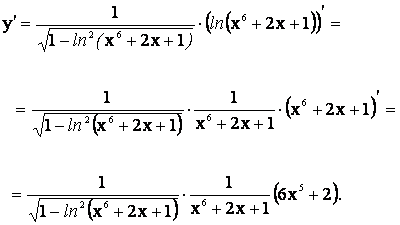
3.2. Исследование функции.
Если функция f(x) задана аналитически, то ее исследование можно
проводить по следующей схеме:
1) область определения функции;
2) точка пересечения графика с
осями координат;
3) четность, нечетность;
4) периодичность;
5) промежутки возрастания и
убывания функции;
6) экстремумы функции;
7) интервалы выпуклости,
вогнутости, точки перегиба;
8) асимптоты графика;
9) построение графика
.
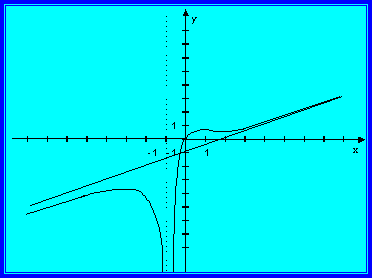
Пример. Провести полное исследование функции и построить
график
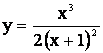 .
.
1) Область
определения функции x + 1 ¹ 0 или x ¹ - 1. Значит, функция
существует при всех значениях x кроме x = -1,
при котором знаменатель дроби обращается в нуль, т.е. x Î (-¥, -1) È (-1, +¥).
2)
Точки пересечения с осями
координат
у(0)= ,
,
следовательно, линия пересекает оси в точке (0, 0).
3) Четность или нечетность:
 .
.
Следовательно, заданная
функция свойством четности не обладает, т.е. является функцией общего вида.
4) Периодичность: определяем
только для тригонометрических функций.
5) Промежутки возрастания и убывания функции: находим первую производную
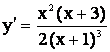
Определим критические точки, для этого решаем
уравнение у¢ = 0 или
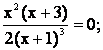
х2(х + 3) = 0;
х1 = 0, х2 = -3.
Используя метод интервалов, определим промежутки
монотонности
-3 -1
х

Функция возрастает на промежутке х Î (-¥,-3] È [-1, ¥) и убывает при х Î [-3, -1).
6) Так как производная
функции меняет знак с “+” на “-” в точке х = -3, то функция имеет max в этой
точке и уmax = y(-3) = -27/8. Точка х = -1
является точкой разрыва функции и не входит в область ее определения. Поэтому,
несмотря на то, что производная в этой точке меняет знак с “-” на “+ экстремума
здесь нет.
7) Интервалы вогнутости,
выпуклости. Найдем вторую производную функции и решим уравнение у¢¢ = 0. Несложно показать, что
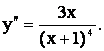
Приравнивая числитель к нулю, получаем: х = 0.
Критическая точка х = 0 разбивает область определения ]-¥, -1[ È ]-1, +¥[ на интервалы: ]-¥, -1[ È ]-1, 0[ È ]0, +¥[.
-1
0
х

Т
Таким образом, на интервалах
]-¥, -1[ È ]-1, 0[ функция выпуклая,
на интевале ]0, +¥[ - вогнутая.
8) Асимптоты:
а) горзонтальная асимптота определяется
с помощью предела
![]() .
.
Так
как предел равен ± ¥, то горизонтальной
асимптоты нет.
б) вертикальную асимптоту можно определить из области определения функции. Так как точка х = -1 является точкой разрыва, то прямая х = -1 есть вертикальная асимптота. Найдем лево - и правосторонние пределы
 .
.
в) уравнение наклонной асимптоты ищем в виде у = kх + b, где

Тогда,
прямая 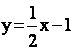 - наклонная асимптота.
- наклонная асимптота.
9) Строим чертеж
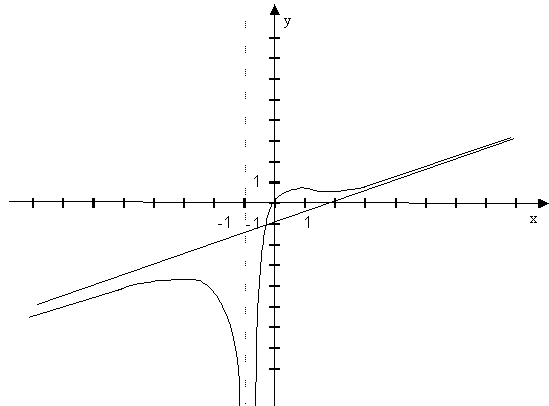
4.
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
4.1. Неопределенные интегралы
Функция F(x) называется первообразной для функции f(x) на некотором промежутке [a, b], если для всех значений x из этого промежутка справедливо равенство F¢(x) = f(x). Например, функция F(x) = x2 является первообразной функции f(x) = 2х на всей числовой прямой, т.к. F¢(x) = f(x) для всех х Î (-¥, ¥). Если F(x ) – первообразная для f(x), то, очевидно, F(x) + С, где С –произвольная константа, также является первообразной для f(x). Пусть функция F(x) - первообразная для функции f(x) на некотором промежутке [a, b], тогда множество функций F(x)+С, где С - произвольная постоянная, называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается
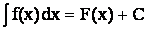 .
.
Вычисление неопределенного
интеграла данной подынтегральной функции f(x) называется интегрированием этой функции. Для того, чтобы
проверить, правильно ли выполнено интегрирование, достаточно
продифференцировать результат и получить подынтегральную функцию.
Основные свойства неопределенного интеграла
1. Производная неопределенного
интеграла равна подынтегральной функции
![]() .
.
2. Неопределенный интеграл от
дифференциала функции F(x) равен F(x)+C
![]() .
.
3. Постоянный множитель можно
вынести из под знака интеграла
![]() .
.
4. Неопределенный интеграл от
алгебраической суммы двух функций равен алгебраической сумме двух интегралов от
этих функций
![]()
5. Если F(x)
является первообразной для f(x), то
![]()
Таблица основных интегралов
1. ![]() .
.
2. ![]()
3. 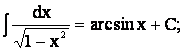
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. 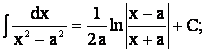
12. 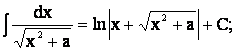
13. ![]()
14. 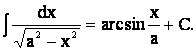
4.2. Основные методы
интегрирования
1. Непосредственное
интегрирование. Вычисление неопределенного интеграла с помощью
непосредственного использования таблицы простейших интегралов и основных
свойств неопределенных интегралов называется непосредственным интегрированием.
Пример. Вычислить интегралы

![]()
2. Метод подстановки (метод замены переменной). Введение новой переменной интегрирования
часто дает возможность свести вычисление данного интеграла к табличному
интегралу. Полагая
x = j(x), получаем
![]()
Пример. Вычислить интегралы 1) 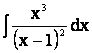 ;
2)
;
2) ![]() .
.
Решение.
1) Полагаем
x – 1 = t, тогда x = t + 1.
Значит, dx = d(t + 1) =
dt и
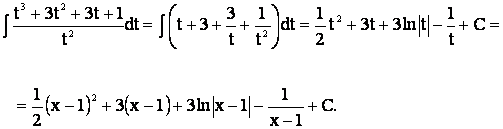
2) Поскольку d(cosx) =
- sinxdx, то
![]() .
.
3. Интегрирование по
частям. Формула интегрирования по частям имеет вид
![]() .
.
Так как v¢(x)dx = dv и u¢(x)dx = du, то формулу интегрирования
по частям можно переписать в виде
![]() .
.
Формула интегрирования по частям позволяет свести
вычисление ![]() к вычислению интеграла
к вычислению интеграла
![]() . При этом за u принимается функция,
которая дифференцированием упрощается, а за dv - часть подынтегрального
выражения, содержащая dx, интеграл от которой может
быть легко вычислен. За u обычно обозначают функции lnx, arctgx, arcsinx.
. При этом за u принимается функция,
которая дифференцированием упрощается, а за dv - часть подынтегрального
выражения, содержащая dx, интеграл от которой может
быть легко вычислен. За u обычно обозначают функции lnx, arctgx, arcsinx.
Пример. Вычислить интегралы


Иногда формулу интегрирования по частям приходится использовать несколько раз.
Пример. Вычислить интеграл:

4.3. Определенный интеграл
Определенным интегралом в
пределах от а до b от функции f(x), непрерывной на отрезке [a, b],
называется приращение любой ее первообразной F(x) при изменение аргумента x от
значения x = a до значения x = b:
![]()
Основные свойства
определенного интеграла
1. Определенный интеграл от алгебраической
суммы конечного числа функций равен алгебраической сумме определенных
интегралов от слагаемых функций:
![]() .
.
2. Постоянный множитель можно
выносить за знак интеграла:
![]()
3. При перестановке пределов интегрирования
определенный интеграл меняет знак на противоположный:
![]()
4. Определенный интеграл с
одинаковыми пределами равен нулю
![]()
5. Отрезок интегрирования можно
разбить на части, т.е. каковы бы ни были числа a, b, c справедливо равенство
![]() .
.
Пусть F(x) - первообразная для f(x), тогда
![]()
Эта формула является
основной формулой интегрального исчисления и называется формулой Ньютона- Лейбница.
Примеры. Вычислить интегралы
1.![]()

2. 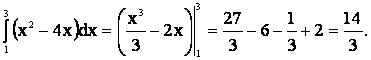
3. ![]()
Также как и неопределенный,
определенный интеграл может быть вычислен методом интегрирования по частям и
заменой переменной.
Формула интегрирования по
частям в определенном интеграле имеет вид
![]() ,
,
при этом функции u(x), v(x) должны быть непрерывно дифференцируемы на интервале [a, b].
Пример. Вычислить ![]() .
.
Решение. Пусть u = lnx, dv = dx, тогда du = d(lnx) = dx/x,
v = х и ![]() . Значит,
. Значит,

Замена переменной в
определенном интеграле
Полагая x = j(u), dx = j¢(u)du, получаем
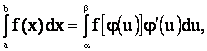
где j(a) = a, j(b) = b.
Пример. Вычислить ![]() .
.
Решение. Пусть x2 + 1 = u тогда du = 2xdx, xdx =
2-1du. Кроме того, если x = 0, то u = 1, если x = 1, то u = 2. Таким
образом, получаем
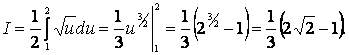 .
.
4.4. Площадь криволинейной трапеции
Пусть на плоскости Oxy дана
фигура, ограниченная кривой y = f(x), и прямыми x = a, x = b (a< b). Площадь такой плоской фигуры находится
по формуле
![]()
При вычислении площади
необходимо соблюдать правило знаков: площади, находящиеся над осью Ox, берутся со знаком плюс, а площади, расположенные
под осью Ox, берутся со знаком минус. Если f(x) конечное число раз меняет знак
на отрезке [a, b], то площадь криволинейной
трапеции можно вычислить по формуле
![]() .
.
Если
площадь ограниченна двумя непрерывными кривыми, уравнения которых y = f1(x),
y = f2(x) и прямыми x = a, x = b (a< b), то площадь определяется
по формуле
![]() .
.
 Пример. Вычислить площадь фигуры,
ограниченной параболой
у = -х2 - 2х + 3 и прямыми х = 0, х = 2, у = 0.
Пример. Вычислить площадь фигуры,
ограниченной параболой
у = -х2 - 2х + 3 и прямыми х = 0, х = 2, у = 0.
Решение. Так как на отрезке [0, 2] функция f(x) = -х2- 2х + 3
меняет знак, а именно f(x) ³ 0 на отрезке [0, 1] и f(x) £ 0 на отрезке [1, 2], то искомую площадь можно вычислить по
формуле
![]() .
.
Тогда
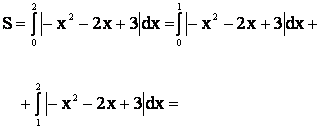
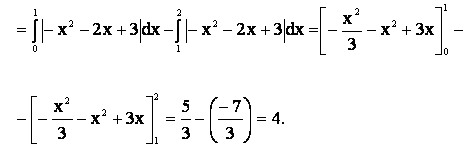
4.5. Несобственные интегралы
1.
Интегралы от неограниченных функций. Пусть
f(x) неограниченна в любой
окрестности точки с отрезка [a, b] и непрерывна в промежутке при a £ x < c и c < x £ b, то, по определению, полагают
![]()
если пределы в правой части равенства существуют и
конечны, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.
2. Интегралы с бесконечными
пределами интегрирования. Пусть функция f(x)
непрерывна при a £ x < ¥, то, полагают,
![]()
Если существует конечный предел в правой части последнего равенства, то такой несобственный интеграл называется сходящимся. Аналогично определяем следующие интегралы
![]() ,
, ![]() ,
,
где с - некоторая точка из интервала (а, b).
Пример. Вычислить интеграл
 .
.
Решение. Так как ![]() , то
, то
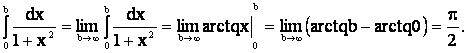
5. ФУНКЦИИ
ДВУХ ПЕРЕМЕННЫХ
Переменная z называется функцией двух переменных x и y, если каждой паре значений x и y в некоторой области их изменения поставлено в соответствие значение z. Функциональную зависимость z от x и y записывают в виде z = f(x, y). Совокупность значений x и y, при которых z = f (x, y) имеет действительные значения, называется областью определения функции z. d - окрестностью точки A0(x0, y0) называется круг с центром в точке A0 радиуса d. Точки, принадлежащие окрестности, удовлетворяют неравенству
(x - x0)2 + (y - y0)2 £ d2.
Постоянное число k называется пределом функции z = f(x, y), если для любой точки B(x, y) из d - окрестности точки A0 выполняется неравенство |k - z| < e, где e > 0. Функция z = f(x, y) называется непрерывной в точке A0(x0,y0), если
![]() ,
,
т.е. предел функции при стремлении к точке A0(x0, y0) равен значению функции в этой точке.
5.1.
Производная, градиент и полный дифференциал функции двух переменных
Дана функция z = f(x, y), непрерывная в некоторой области. В некоторой точке A(x, y) дадим аргументу x приращение Dx, аргумент y остается при этом постоянным.
![]()
Отношение ![]() - называется частной производной функции z по аргументу x.
- называется частной производной функции z по аргументу x.
Аналогично, получаем производную функции z по аргументу y:
![]() .
.
Для вычисления частных производных используем таблицу производных функции одной переменной. Условие неизменности второго аргумента остается в силе только в процессе нахождения производных. Полученные производные вновь являются функциями двух переменных и от каждой из них можно найти по две производные, которые называются частными производными второго порядка

Смешанная вторая производная не зависит от порядка дифференцирования:
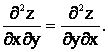
Полный дифференциал функции двух переменных равен сумме его частных дифференциалов
![]()
т.е.
![]() .
.
Выражение
![]()
называется производной функции z = f(x, y) в данном направлении l0(cosa, cosb) (производной по направлению). Градиентом функции z = f(x, y) называется вектор, координатами которого являются частные производные функции
![]() .
.
Производная по направлению градиента имеет наибольшее значение, т.е. градиент – это направление максимального роста функции.
5.2.
Экстремумы функции двух переменных
Пусть функция z = f(x, y) непрерывна в некоторой области D. Точка P0(x0, y0) называется максимумом функции z, если в этой точке функция имеет наибольшее значение по сравнению с точками некоторой ее окрестности
![]() .
.
Точка P0(x0, y0) называется минимумом функции z, если в этой точке функция имеет наименьшее значение по сравнению с точками некоторой ее окрестности
![]()
Если в точке P0(x0, y0) функция z = f(x, y) достигает максимума или минимума, то говорят, что функция z = f(x, y) в точке P0 достигает экстремума, а саму точку называют точкой экстремума. Функцию двух переменных z = f(x, y) исследуем на экстремум по следующим правилам:
1. Находим частные производные первого порядка z¢x и z¢y. Приравниваем их к нулю z¢x = 0, z¢y = 0. Решаем полученную систему уравнений. Решения этой системы являются координатами критических точек (точек, в которых возможен экстремум).
2. Находим частные производные
второго порядка z¢¢xx, z¢¢xy и z¢¢yy. Вычисляем их
значения в каждой критической точке. В точке Р(x0, y0):
![]() ,
, ![]() ,
, ![]() , D
= AC - B2.
, D
= AC - B2.
Если D
>
3. Вычисляем экстремальные значения функции.
Пример. Исследовать на экстремум
функцию z = x3 + y3 - 3xy.
Решение. 1) Находим частные производные первого
порядка
z¢x = 3x2 - 3y; z¢y = 3y2 - 3x.
Приравниваем их
к нулю и решаем систему уравнений
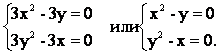
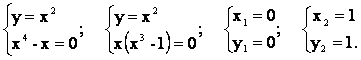
Получили две критические точки P1(0, 0), P2(1,1).
2) Находим частные производные второго порядка:
z¢¢xx = 6x;
z¢¢xy = -3; z¢¢yy = 6y.
Вычисляем их значения в каждой критической точке.
Точка P1(0,
0):
A = 6×0 = 0;
B = -3; C = 6×0 = 0. D = 0×0-9 = -9 < 0.
B точке P1(0, 0) экстремума нет.
Точка P2(1,
1):
A = 6×1 = 6;
B = -3; C = 6×1 = 6. D = 6×6 – 9 = 27.
В точке P2(1, 1) (A >
3) zmin= 13 + 13 - 3×1×1 = -1.
Ответ:
в точке P(1, 1) функция принимает минимальное значение zmin = -1.
Метод наименьших квадратов.
Часто при решении практических задач возникает необходимость установить
аналитическую зависимость между двумя величинами, значения которых получены
экспериментально. Пусть эти
значения сведены в таблицу.
|
xi |
х1 |
x2 |
x3 |
… |
xn |
|
yi |
y1 |
y2 |
y3 |
… |
yn |
Наносим точки (xi, yi) из таблицы на координатную плоскость. Предположим, что точки расположены вблизи прямой линии y = ax + b.
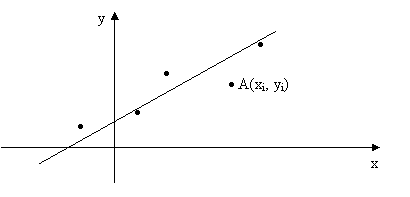
Возьмем точку Ai(xi, yi). На прямой линии ей соответствует точка Вi(xi, ax i + bi). Разность между ординатами этих точек составляет погрешность [yi- (axi + b)].Сумма квадратов этих погрешностей составляет функцию:
![]() .
.
Найдем ее минимум. Находим частные производные первого порядка и приравниваем их к 0. После преобразований получаем систему уравнений

относительно a и b. Эта система имеет единственное решение (a¢, b¢)и в этой точке функция S(a, b) имеет минимум.
Пример. Полученные из опыта значения двух переменных x, y приведены в таблице
|
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
1,9 |
7,1 |
11,8 |
17,2 |
21,9 |
Построив точки на координатной плоскости, видим, что они расположены вблизи прямой линии. Уравнение прямой y = ax + b. Составляем расчетную таблицу
|
i |
xi |
yi |
xi2 |
xiyi |
|
1 |
1 |
1,9 |
1 |
1,9 |
|
2 |
2 |
7,1 |
4 |
14,2 |
|
3 |
3 |
11,8 |
9 |
35,4 |
|
4 |
4 |
17,2 |
16 |
69,2 |
|
5 |
5 |
21,9 |
25 |
109,5 |
|
å |
15 |
60,0 |
55 |
230,2 |
Получаем систему:

Решив ее, находим а = 5,05, b = -3,15. Уравнение искомой прямой y = 5,05x - 3,15.
6. ЛИНЕЙНАЯ АЛГЕБРА
6.1.
Матрицы
Система элементов (чисел, функций) расположенных в виде прямоугольной таблицы, состоящей из m строк и n столбцов, называется прямоугольной матрицей размерности m ґ n:
А= ,
,
где aij –элементы матрицы (i = 1, 2,…, m; j = 1, 2, …, n). Сокращенная запись матрицы: A = (aij)m´n. Если m = n, то матрица называется квадратной. В этом случае число m = n называют ее порядком. В квадратной матрице n-го порядка диагональ, состоящая из элементов a11, a22 ,…, ann называется главной диагональю. Если в квадратной матрице все элементы, стоящие на главной диагонали, равны единице, а остальные элементы равны нулю, то такая матрица называется единичной и обозначается Е. Например, единичная матрица четвертого порядка имеет вид

Две матрицы A = (aij)m´n и В = (bij)m´n одинаковой размерности называются равными, если равны элементы, стоящие на одинаковых местах этих матриц. Над матрицами можно выполнять действия: сложение (вычитание), умножение на число, умножение двух матриц, транспонирование.
Суммой (разностью) двух матриц A = (aij)m´n. и В = (bij)m´n. одинаковой размерности называется матрица С, элементы которой определяются равенством
сij = aij ±
bij (i = 1, 2, …, m; j = 1, 2, …, n).
Обозначение: А ± В = С.
Произведением матрицы A = (aij) m´n на число к называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы А на число к:
Aк = к(aij)m´n = (кaij) m´n
(i = 1, 2,
…, m; j = 1, 2, …, n).
Произведением АВ матрицы A = (aij)m´n на матрицу В = (bij)n ´k называется матрица C = (cij)m´k, где элемент cij равен сумме произведений элементов i-ой стороки матрицы А на соответствующие элементы j-го столбца матрицы В, т.е.
cij = (ai1, ai2 , … , ain)(b1j, b2j, … , bnj) = ai1b1j+ ai2b2j+… + ainbnj.
(i = 1, 2, …, m; j = 1, 2, …, n).
Произведение матрицы А на матрицу В определено только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. Матрица, полученная из матрицы А заменой всех строк соответствующими по номеру столбцами, называется транспонированной по отношению к А и обозначается АТ, т.е.

Пример. Даны матрицы
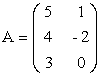 ,
, 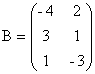
Найти А + С; 2А.
Решение. Так как при сложении матриц складываются соответствующие элементы, то
А + В =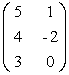 +
+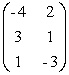 =
=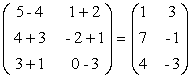 .
.
При умножении матрицы на число нужно каждый элемент
матрицы умножить на это число:
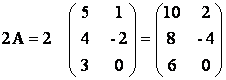 .
.
Пример. Даны матрицы
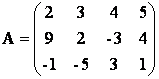
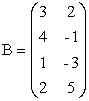 .
.
Найти произведение АВ.
Решение. Размерность матрицы А – (3х4), а матрицы В – (4х2) ,т.е. число столбцов матрицы А равно числу строк матрицы В, следовательно АВ существует. Заметим, что так как число столбцов матрицы В не равно числу строк матрицы А, то В×А не существует.
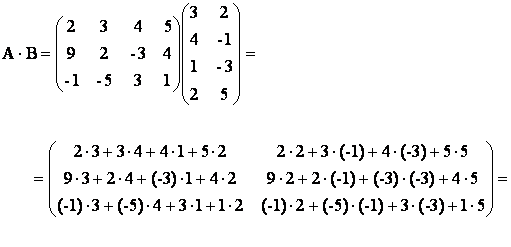
 .
.
6.2.
Определители
Определителем n-го порядка (n і 2) называется число, обозначаемое
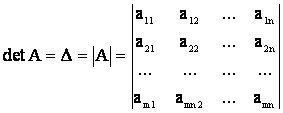
и равное алгебраической сумме n! членов, каждый из которых равен произведению n элементов, взятых по одному из каждой строки и каждого столбца.
Минором Mik элемента аik, определителя n - го порядка называется определитель (n - 1) - го порядка, получающийся из данного определителя в результате вычеркивания i-й строки и j-го столбца, на пересечении которых стоит данный элемент. Алгебраическим дополнением А1j элемента аik, определителя называется число Аik = (-1)i+kMik,. Определитель n - го порядка (n і 2) вычисляют разложением по элементам первой строки по формуле
![]()
где а1i (i = 1, …, n) – элементы первой строки, А1j (i = 1, …, n) - алгебраические дополнения этих элементов. Если n = 2, то имеем определитель второго порядка
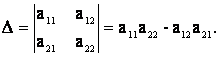
При n = 3 получим определитель 3-го порядка
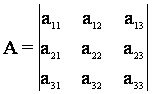 ,
,
каждый член которого равен произведению трех элементов, взятых по одному из каждого столбца и каждой строки; число членов равно n! = 1×2×3 = 6. Определитель 3-го порядка можно вычислить по треугольной схеме (правило Саррюса). Если соединить линией каждые три элемента определителя (по одному из каждой строки и каждого столбца), то получим легко запоминающуюся схему
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()

Пример. Вычислить определитель
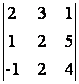 .
.
Решение. Вычислим определитель по правилу Саррюса:
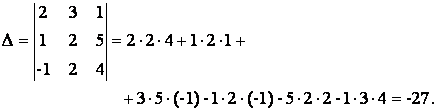
6.3. Основные
свойства определителей
1. При транспонировании определителя его величина не изменяется.
2. Если поменять местами любые две строки или два столбца, то определитель изменит свой знак.
3. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
4. Определитель равен нулю, если все элементы какой-нибудь строки (столбца) равны нулю, или имеются две одинаковые или две пропорциональные строки (столбца).
5. Величина определителя не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.
Из свойств определителей следует, что все строки и столбцы определителя равноправны. Поэтому определитель n - го порядка можно вычислить разложением по любой строке (столбцу). Используя свойство 5, можно преобразовать определитель так, чтобы в выбранной строке (столбце) все элементы, кроме одного, были равны нулю. Тогда вычисление определителя n-го порядка сводится к вычислению единственного определителя (n - 1)-го порядка. Покажем это на примере.
Пример. Вычислить определитель

Решение. При получении нулей в строке (столбце) удобно использовать любой элемент аik = ± 1. Разложим определитель по элементам второй строки (здесь есть элемент а23 = 1). Обратим элементы а21, а22, а24, в нули. Для этого все элементы 3-го столбца умножим на (-2) и прибавим к соответствующим элементам 1-го столбца, затем умножим 3-й столбец на (-1) и прибавим ко 2-му, умножив 3- й столбец на (-2), прибавим его к 4-ому.
![]()
![]()

6.4.
Матрица, обратная данной
Матрица А-1 называется обратной по отношению к матрице А, если
А-1А = А А-1 = Е,
где Е- единичная матрица. Для любой квадратной матрицы А, определитель которой отличен от нуля, существует единственная обратная матрица, которую находят по формуле
А-1 =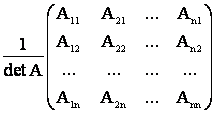 ,
,
где Аik – алгебраические дополнения элементов аik , detА - определитель исходной матрицы А.
Пример. Выяснить, существует ли матрица, обратная данной

и если существует, найти ее. Сделать проверку.
Решение. Найдем определитель матрицы А.

Поскольку detА № 0, то существует обратная матрица А-1. Найдем алгебраические дополнения для
каждого элемента А.
А11 =
(-1)1+1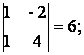 А12
= (-1)1+2
А12
= (-1)1+2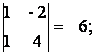
А13 =
(-1)1+3 А21 = (-1)2+1
А21 = (-1)2+1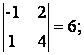
А22 =
(-1)2+2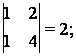 А23 = (-1)2+3
А23 = (-1)2+3
А31 =
(-1)3+1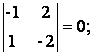 А32
= (-1)3+2
А32
= (-1)3+2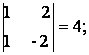
А33 =
(-1)3+3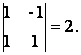
Тогда
А-1= .
.
Проверим, правильно ли найдена матрица А-1:
A×А-1 =
=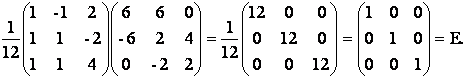
Проверка показывает, что обратная матрица найдена верно.
6.5.
Ранг матрицы
Рангом матрицы называется порядок ее наивысшего минора отличного от нуля. Если ранг матрицы равен r, то это означает, что в матрице А имеется хотя бы один отличный от нуля минор порядка r, но всякий минор порядка, большего чем r равен нулю. Ранг матрицы А обозначают r(А). При определении ранга матрицы приходится вычислять большое число определителей. Чтобы облегчить этот процесс, пользуются элементарными преобразованиями матриц, которые не изменяют ее ранга.
Элементарные преобразования матрицы
1. Перестановка строк (столбцов);
2. Умножение строки (столбца) на число, отличное от нуля;
3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на некоторое число;
4. Отбрасывание строк (столбцов), все элементы которых равны нулю.
Пример. Вычислить ранг матрицы, используя определение
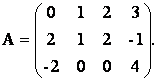
Решение. Среди миноров первого порядка есть
отличные от нуля, так как матрица не нулевая. Среди миноров второго порядка
есть также миноры, отличные от нуля, например 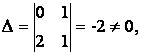 стоящий в левом
верхнем углу.
стоящий в левом
верхнем углу.
Найдем миноры третьего порядка, заключающие минор D:
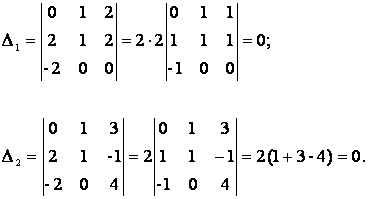
Минор второго порядка  , а все миноры более высоких порядков равны нулю, значит,
ранг матрицы r(A) = 2.
, а все миноры более высоких порядков равны нулю, значит,
ранг матрицы r(A) = 2.
Пример. Вычислить ранг матрицы из предыдущего примера с помощью элементарных преобразований.
Решение.

Так как минор второго порядка  , а все миноры более высоких порядков равны нулю, то ранг матрицы r(A) = 2.
, а все миноры более высоких порядков равны нулю, то ранг матрицы r(A) = 2.
6.6.
Системы линейных уравнений
Общий вид системы

или в матричной форме: АХ = В, где
![]()
 ,
, 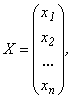 ,
, 
Расширенная матрица системы имеет вид:
![]()

Согласно
теореме Кронекера-Капелли, для того, чтобы система уравнений была совместна,
необходимо и достаточно, чтобы r(A)
= r(A).
При этом, если r(A) = r(`A) = n. где n – число неизвестных, то система имеет единственное решение; если r(A) = r(`A) < n, то система имеет бесчисленное множество решений; если r(A) ¹ r(`A), то система несовместна.
6.7.
Методы решения систем.
Правило Крамера. Неизвестные х1 ,х2 , ….,хn можно найти по формулам Крамера
![]() ,
,
где D-определитель системы, составленный из коэффициентов при неизвестных системы, а Dк (к = 1, 2, …, n) – определитель , полученный из D заменой k - ого столбца столбцом из свободных членов системы. Система имеет единственное решение, если D № 0.
Матричный метод (метод обратной матрицы). Из записи системы уравнений в матричном виде АХ = В следует, что Х = А-1В. Суть метода заключается в нахождении обратной матрицы А-1 и умножении ее на столбец из свободных членов В. Используется для систем уравнений, у которых m = n и detA № 0.
Метод Гаусса. Это метод последовательного исключения неизвестных. Суть метода: с помощью элементарных преобразований строк расширенной матрицы, матрица`А приводится к трапецеидальной форме. Этой матрице ставится в соответствие система, эквивалентная исходной. Решение ее осуществляется снизу вверх (обратный ход метода Гаусса).
Метод Жордана-Гаусса (модификация метода Гаусса). Для упрощения нахождения решений расширенную матрицу данной системы приводят к диагональному виду, исключая неизвестные не только из последующих уравнений, но и из предыдущих.
Пример. Решить систему уравнений тремя способами:
1) методом Крамера;
2) матричным способом;
3) методом Гаусса.
 .
.
1) Решение системы методом Крамера.
Составим определитель из коэффициентов при неизвестных
D=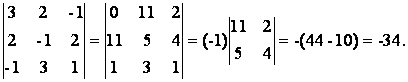
Т.к. D = кАк = -34 № 0, то существует единственное решение системы. Найдем определители D1, D2, D3, заменяя в определителе D соответствующий столбец столбцом из свободных членов.
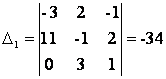 ,
, 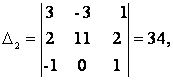

Согласно формул Крамера:
![]()
2) Решение системы матричным способом.
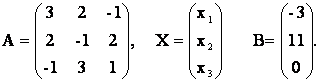
Из матричного уравнения следует, что Х = А-1В. Выше было показано, что D = кАк = -34 № № 0. Т.к. D № 0, то обратная матрица А-1 существует. Найдем алгебраические дополнения:

Отсюда
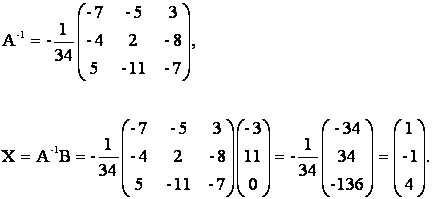
Значит, х1 = 1, х2 = -1, х3 = 4.
3). Решение системы методом Гаусса. Запишем расширенную матрицу системы и приведем ее к трапецеидальной форме с помощью элементарных преобразований матрицы, выполняемых над строками:
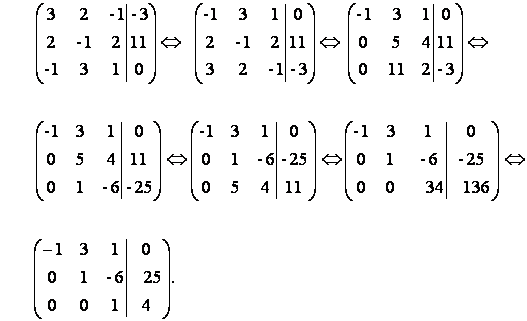
Ставим в соответствие этой расширенной матрице систему, эквивалентную исходной и находим ее решение

Таким образом, решение системы: х1 = 1, х2
= -1, х3 = 4.
Для проверки правильности решения подставим полученные значения х1, х2, х3 в исходную систему.

Система решена верно.
Ответ: х1 =
1, х2 = -1, х3 = 4.
3а) Решение системы методом Жордана-Гаусса. Для упрощения нахождения решений системы расширенную матрицу приводят к диагональному виду, исключая неизвестные не только из предыдущих уравнений, но и из последующих.

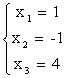
Таким образом, решение системы: х1 = 1, х2 = -1, х3 = -4.
Пример. Исследовать совместность системы и в случае
совместности найти общее решение и частное решение
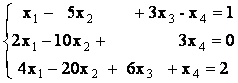
Решение. Выпишем расширенную матрицу
системы и будем выполнять элементарные преобразования ее строк
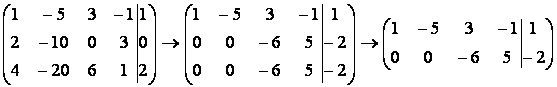 ,
,
r(A) = r(`A) = 2 < n = 4, где n - число неизвестных. Т.к. r(A) = r(`A),
то система совместна, а т.к. ранг меньше числа неизвестных, то система
неопределена. Минор 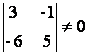 , значит его можно принять в качестве базисного
минора. Тогда неизвестные, коэффициенты которых входят в этот минор, являются
базисными. Таким образом, х3 и х4 – базисные неизвестные,
а х1, х2 – свободные.
, значит его можно принять в качестве базисного
минора. Тогда неизвестные, коэффициенты которых входят в этот минор, являются
базисными. Таким образом, х3 и х4 – базисные неизвестные,
а х1, х2 – свободные.
Запишем систему уравнений, соответствующую преобразованной расширенной матрице:

Выразим базисные неизвестные х3 и х4
через свободные х1 и х2

![]() .
.![]()
Получаем общее решение
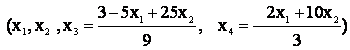 .
.
Придавая свободным неизвестным произвольные числовые значения, например х1 = 1, х2 = -2, получим: х3 = -52/9, х4 = -22/3. Тогда частное решение системы - (1,-2,-52/9, -22/3).
6.8. n-мерные вектора. Действия над векторами
Упорядоченная совокупность n действительных чисел х1, х2,…, хn, называется n – мерным вектором:
`х = (х1, х2, …, хn).
Числа х1, х2,…,хn – координаты вектора. Количество координат определяет размерность
вектора. Суммой (разностью) двух
векторов ` х = (х1, х2,
…, хn) и ![]() называется
вектор вида
называется
вектор вида ![]() . Умножение вектора
. Умножение вектора ![]() на число к определено так
на число к определено так ![]() . Множество всех n–мерных векторов, для которых
определены операции сложения и умножения на число, называется арифметическим векторным пространством и обозначается Rn.
. Множество всех n–мерных векторов, для которых
определены операции сложения и умножения на число, называется арифметическим векторным пространством и обозначается Rn.
Скалярным произведением двух n – мерных векторов ![]() и
и ![]() называют число,
определяемое формулой
называют число,
определяемое формулой ![]() .
.
6.9.
Линейная зависимость векторов. Базис. Разложение вектора
по
базису
Вектор ![]() , где
, где ![]() - числа, называется линейной
комбинацией векторов
- числа, называется линейной
комбинацией векторов ![]() . Векторы
. Векторы ![]() называется линейно-зависимыми, если существуют
такие числа
называется линейно-зависимыми, если существуют
такие числа ![]() , не все равные нулю, что
, не все равные нулю, что ![]() . Если же это равенство возможно в единственном случае,
когда
. Если же это равенство возможно в единственном случае,
когда ![]() то векторы
то векторы ![]() называются линейно независимыми. Векторы n –
мерного пространства
называются линейно независимыми. Векторы n –
мерного пространства
![]()
![]()
…
![]()
линейно независимы, если определитель, составленный из координат этих векторов, отличен от нуля, т.е.

Любая система n – линейно независимых векторов n- мерного пространства называется базисом этого пространства. Из этого определения следует, что любая система n- мерных векторов
![]()
![]()
…
![]() .
.
образует базис n- мерного пространства, если определитель, составленный из их координат, не равен нулю. Всякий вектор n- мерного пространства разлагается по векторам любого базиса этого пространства, и притом единственным образом по формуле
![]() ,
,
где ![]() образуют базис
n- мерного пространства, ``b
- вектор этого пространства, не принадлежащий базису. Коэффициенты этого разложения
являются координатами вектора`
`b в этом пространстве, т.е.
образуют базис
n- мерного пространства, ``b
- вектор этого пространства, не принадлежащий базису. Коэффициенты этого разложения
являются координатами вектора`
`b в этом пространстве, т.е. ![]() .
.
Пример. Проверить, что векторы
![]()
образуют базис в R3. Найти координаты вектора ![]() в этом базисе.
в этом базисе.
Решение. Покажем, что векторы ![]() образуют базис в
R3 . Составим определитель из координат векторов.
образуют базис в
R3 . Составим определитель из координат векторов.
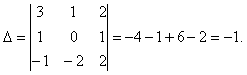
Так как D = -1 №
0, то векторы ![]() -
линейно независимы, а значит, образуют базис в R3. Вектор ``b не принадлежит
этому базису, поэтому его можно единственным образом разложить по базису
-
линейно независимы, а значит, образуют базис в R3. Вектор ``b не принадлежит
этому базису, поэтому его можно единственным образом разложить по базису ![]() .
.
![]()
получаем следующую систему линейных уравнений
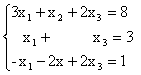
Решим систему методом Гаусса. Выпишем расширенную матрицу системы и произведем над ней элементарные преобразования:
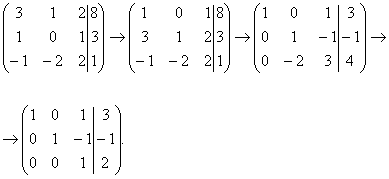
Последней матрице соответствует система, эквивалентная исходной

х3 = 2, х2 = -1 + х3 = -1 + 2 =!, х1 = 3 - х3 = 3 – 2 = 1.
Итак, ![]() . Значит в базисе
. Значит в базисе ![]() вектор ``b имеет координаты
вектор ``b имеет координаты ![]()
8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
При проведении научных исследований не всегда
можно установить непосредственно характер зависимости между переменными х и у,
но можно определить зависимость между х и у, у¢,…,у(n).
Уравнение вида F(x, y
,у¢, …, у(n))
= 0, связывающее независимую переменную х с искомой функцией у и ее
производными у¢, …, у(n),
называются дифференциальными. Порядком дифференциального уравнения
называется порядок наивысшей производной, входящей в это уравнение. Например, у¢ = 2x - дифференциальное уравнение
первого порядка; y¢¢ + у¢ - x = 0 - дифференциальное
уравнение второго порядка.
Решением дифференциального уравнения называется функция j(x), которая удовлетворяет
данному уравнению, т.е. при подстановке y, у¢ = j¢(x), …, y(n)
= j(n)
уравнение превращается в тождество. Методы решения дифференциальных уравнений
тесно связаны с порядком уравнения и видом зависимости между переменными.
8.1.
Дифференциальные уравнения первого порядка
Дифференциальное
уравнение первого порядка имеет вид
F(x, y, y¢) = 0.
Если его разрешить относительно y¢, то можно найти приведенную
форму дифференциального уравнения первого порядка
y¢ = f(x, y).
Например, решением уравнения y¢ = 2x является функция у = х2,
но его решениями также будут функции у = х2-3, у = х2+![]() и т.д., т.е, все возможные решения этого уравнения имеют вид у = х2+С,
где С – произвольная постоянная. Общим
решением дифференциального уравнения первого порядка называется функция у =
j(x, С), которая удовлетворяет
дифференциальному уравнению при любом значении константы С. Если в процессе
решения дифференциального уравнения получаем соотношение вида
и т.д., т.е, все возможные решения этого уравнения имеют вид у = х2+С,
где С – произвольная постоянная. Общим
решением дифференциального уравнения первого порядка называется функция у =
j(x, С), которая удовлетворяет
дифференциальному уравнению при любом значении константы С. Если в процессе
решения дифференциального уравнения получаем соотношение вида
Ф(х, у, С) = 0,
т.е. неявное задание функции у, то его называют общим интегралом. Частным решением дифференциального уравнения называется любая
функция у = j(х, С0), полученная из общего
решения у = j(х, С), если произвольной постоянной С
придается конкретное значение С = С0.
Теорема. Если в уравнении y¢ = f(x, y) функции f(x, y) и ![]() непрерывны в некоторой области D и
точке (х0, у0) Î D, то существует единственное
решение этого уравнения у = j(x), такое, что у0 =
j(x0).
непрерывны в некоторой области D и
точке (х0, у0) Î D, то существует единственное
решение этого уравнения у = j(x), такое, что у0 =
j(x0).
Условие,
вида: у = у0 при х = х0 называется начальным условием (или условием Коши). Если известно общее решение
уравнения и начальное условие, то значение С0 является решением
уравнения у = j(x0, С).
8.2. Дифференциальное уравнение с разделенными и
разделяющимися переменными
Если для уравнения вида у¢ = f(x, y), правая часть имеет
вид f(x, y) = f1(x)×f2(y), то соответствующее
уравнение называется уравнением с
разделяющимися переменными и поскольку ![]() , то уравнение можно записать в виде уравнения с разделенными переменными.
, то уравнение можно записать в виде уравнения с разделенными переменными.
![]() .
.
Это уравнение можно рассматривать как равенство двух дифференциалов. Вычислив первообразные правой и левой части
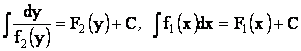 ,
,
получаем общий интеграл F2(y) = F1(x) + C.
Пример. Найти частное решение дифференциального уравнения ![]() , удовлетворяющее начальным условиям х0 = 2, у0
= 3.
, удовлетворяющее начальным условиям х0 = 2, у0
= 3.
Решение. Разрешая уравнение относительно у¢, получим
![]() .
.
Поскольку ![]() , т.е.
, т.е. ![]() , f2(у) = у, то данное уравнение является
уравнением с разделяющимися переменными, его можно записать в виде уравнения с
разделенными переменными
, f2(у) = у, то данное уравнение является
уравнением с разделяющимися переменными, его можно записать в виде уравнения с
разделенными переменными
![]()
Проинтегрируем
обе части последнего равенства
![]()
или
ln|y| = ln|1 + x2| + lnC.
Упрощая, имеем y = C(1 + x2) - общее уравнение.
Подставив начальное условие, находим 3 = С(1 + 22), С = 3/5.
Окончательно, искомое частное решение у = 3(1 + х2)/5.
8.3.Линейные дифференциальные уравнения первого
порядка
Линейным называется дифференциальное уравнение линейное относительно у и у¢, т.е. его вид
у¢+Р(х)у=Q(x),
где Q(x) и Р(х)- непрерывные по х
функции. Если Q(x) º 0, то уравнение у¢ + Р(х)у = 0 называется однородным, если Q(x) ¹ 0, то уравнение – неоднородное. Однородные линейные уравнения являются одновременно уравнения с
разделяющимися переменными, а неоднородные решают с помощью замены
![]() .
.
Пример. Найти частное решение уравнения ху¢ + у = 1/(1 + х), при х0
= 1, у0 = ln2.
Решение. Разделим обе части
равенства на х.
у¢+![]() у =
у =![]() ,
,
т.е. Р(х) = 1/х и Q(x) =![]() . Следовательно, замена имеет вид y = ue-lnx =
u/x. Тогда у¢=
. Следовательно, замена имеет вид y = ue-lnx =
u/x. Тогда у¢=![]() -
-![]() . Подставив в исходное уравнение, получим
. Подставив в исходное уравнение, получим
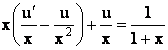
или после упрощения
u¢=![]() ,
,
![]()
Общее решение исходного уравнения имеет вид
![]() .
.
Найдем константу С: ln2 = ln|1 +
1| + C, т.е. С = 0. Подставим начальные условия в общее решение, тогда
частное решение
![]()
В некоторых случаях, если точное решение
дифференциального уравнения громоздко или трудно определимо, можно найти
приближенное решение, используя ряды Тейлора или Маклорена. Проиллюстрируем
применение этого метода на примере.
Пример. Найти три ненулевых члена разложения в ряд частного решения уравнения
ху¢ + у = 1/(1 + х), х0 =
1, у0 = ln2.
Решение. Поскольку х0 =
1, то полученное разложение будет разложением в ряд Тейлора по степеням (х - х0),
для данного случая – (х - 1).
![]() .
.
Запишем уравнение в приведенной форме у¢ = ![]() -
- ![]() . Подставив начальные условия, находим
. Подставив начальные условия, находим
![]() .
.
По
определению у¢¢ = (у¢)¢ = 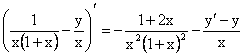 и, используя известные
значения х0, у0, у¢0 получаем у¢¢0 = -3/4 - ½ + 2ln2 =
-5/4 + 2ln2. Отсюда
и, используя известные
значения х0, у0, у¢0 получаем у¢¢0 = -3/4 - ½ + 2ln2 =
-5/4 + 2ln2. Отсюда
у = ln2 + (![]() - ln2)(х - 1) + (2ln2 -
- ln2)(х - 1) + (2ln2 - ![]() )
)![]() +…
+…
ЗАДАНИЕ 1
Даны вершины А(х1,у2)
В(х2,у2), С(х3,у3) треугольника.
Найти:
1) периметр треугольника;
2) уравнение высоты, проходящей через вершину А;
3) уравнение прямой, проходящей
через точку А параллельно прямой ВС;
4) уравнение медианы,
проведенной через вершину А;
5) угол, образованный медианой, проведенной из
вершины А, и стороной АВ;
6) площадь треугольника АВС;
7) систему линейных неравенств, определяющих
треугольник АВС. Сделать чертеж.
|
1. |
А(1,0),
В(7,3), С(4,4) |
|
14. |
А(-3,1), В(3,4),
С(0,5) |
|
2. |
А(1,-2),
В(-5,1), С(-2,2) |
15. |
А(-1,-3), В(5,0),
С(2,3) |
|
|
3. |
А(-1,-1),
В(5,2), С(2,3) |
16. |
А(2,-1), В(-4,2), С(-1,3) |
|
|
4. |
А(1,-1),
В(-5,2), С(-2,3) |
17. |
А(-1,-1), В(5,2),
С(2,5) |
|
|
5. |
А(1,-1),
В(7,2), С(4,5) |
18. |
А(-1,2), В(5,5),
С(2,6) |
|
|
6. |
А(-1,1),
В(-7,4), С(-4,5) |
19. |
А(-4,0), В(2,3),
С(-1,4) |
|
|
7. |
А(-1,1), В(5,4),
С(2,5) |
20. |
А(-1,0), В(5,3),
С(2,6) |
|
|
8. |
А(1,1),
В(-5,4), С(-2,5) |
21. |
А(0,-1), В(-6,2),
С(-3,3) |
|
|
9. |
А(1,1), В(7,4),
С(4,5) |
22. |
А(2,0), В(-4,3),
С(-1,4) |
|
|
10. |
А(-1,-1), В(-7,2),
С(-4,3) |
23. |
А(3,1), В(-3,-2),
С(0,-3) |
|
|
11. |
А(-1,-1), В(-7,2),
С(-4,3) |
24. |
А(3,-2), В(9,1),
С(6,4) |
|
|
12. |
А(-2,2), В(4,1),
С(1,2) |
25. |
А(-2,-1), В(4,2),
С(1,3) |
|
|
13. |
А(3,1), В(-3,4),
С(0,5) |
|
|
ЗАДАНИЕ 2
Продифференцировать заданные функции:
|
1. |
у
= (34x - 1) |
|
у = arctg ln(x - cosx) |
|
2. |
у = 6 |
|
у =
ln(e-2x + xe-2x) |
|
3. |
у = e-3xsin4x |
|
у = |
|
4. |
у =
(3x + log34x)2 |
|
у = ln3 |
|
5. |
у = |
|
у = arctg( |
|
6. |
у
= x3 |
|
|
|
7. |
у = (x2 + log2x)-2 |
|
у = ln |
|
8. |
у =
(5x2 - 3x)3 - |
|
у = arccos |
|
9. |
у = |
|
у = ln |
|
10. |
у = 12x3arctg |
|
у = arcsin |
|
11. |
у = cos(1
- 3x) |
|
у =
ln(1 + cos-12x) + e5x |
|
12. |
у = xlog2(3x + 1) |
|
у = ln(3
+ x + |
|
13. |
у = sin5xe3x |
|
|
|
14. |
у = x5 |
|
у =
ln(x + |
|
15. |
у = xecos5x |
|
у = sin3cos4x + cos-2x |
|
16. |
у = 5ctg2x
cos4x |
|
у = arcsinln3x + 1/(1 + x2) |
|
17. |
у = 32xtq5x |
|
у = 2lntqx - 1/(sin2x) |
|
18. |
у = e-2xlnx |
|
у = (x2 + 4)sin3x + 7-3x |
|
19. |
у = |
|
у = 1/3sin3(6cos2x + 7) |
|
20. |
у =
sinxcos3x |
|
у = (5x2 - 3x)3 - |
|
21. |
у = |
|
у = tq2x - ctqx2 |
|
22. |
y = (2
+ x) |
у = |
у = arcctgx |
|
23. |
у = |
у = |
у
= arcsin(lnx)
+ esin3x |
|
24. |
у = х |
у = |
у =
arccos2x + 2 |
|
25. |
|
|
|
ЗАДАНИЕ 3
Вычислить пределы:
1. 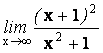
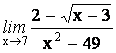
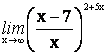
2. 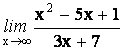
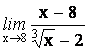

![]()
3. ![]()
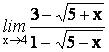
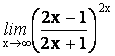
4. 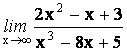
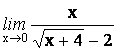
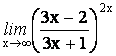
5. 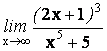
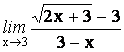
![]()
6. 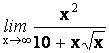

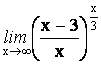
7. 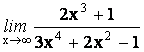
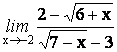
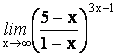
8. 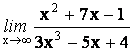
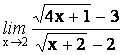
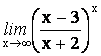
9. 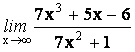

![]()
10. 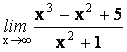
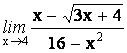
![]()
11. 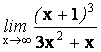
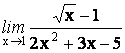
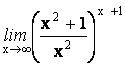
12. 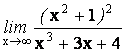

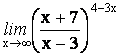
13. ![]()

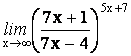
14. 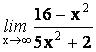
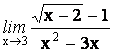
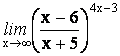
15. 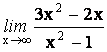


16. ![]()


17. ![]()
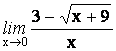
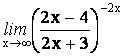
18. 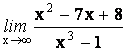


19. ![]()
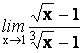

20. 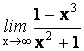
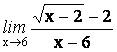

21. 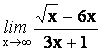


22. ![]()
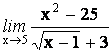
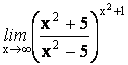
23. 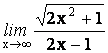


24. 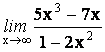
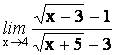

25. 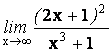
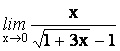
![]()
ЗАДАНИЕ 4
Исследовать
функции методами дифференциального исчисления и построить графики.
|
1. |
у = х2 + 2/х |
14. |
у = х / (х2 -
4) |
|
2. |
у = (х2 - 2х +
2) / (х - 1) |
15. |
у = 5х / (х2 + 3) |
|
3. |
у = (3х4 + 1)/х3 |
16. |
у = (х4 - 3) /
х |
|
4. |
у = 16 / (х2(х - 4)) |
17. |
у = х2 + 1 / х2 |
|
5. |
у = х / (5+х2) |
18. |
у = х3 / (3 – х2) |
|
6. |
у = (х2 - 1) / (х + 2) |
19. |
у = 1 / х +4х2 |
|
7. |
у = х + 4 / (х + 2) |
20. |
у = х4 (х3
– 1) |
|
8. |
у = 4 / х + 1 / х4 |
21. |
у = 3 / х – 1 / х2 |
|
9. |
у = 2 + 12 / (х2 - 4) |
22. |
у = х + х / (3х – 1) |
|
10. |
у = (1 - х3) / х2 |
23. |
у = 4 + х) /х2 |
|
11. |
у = 2х3 / (х2 + 1) |
24. |
у = (х + 1)2 / (х – 2) |
|
12. |
у = 16х / (х – 1)3 |
25. |
у = х + 4 / (х + 2) |
|
13. |
у = 16 / (х2(х – 4)) |
|
|
ЗАДАНИЕ 5
Вычислить
интегралы.
|
1. |
|
|
|
|
2 |
|
|
|
|
3. |
|
|
|
|
4. |
|
|
|
|
5. |
|
|
|
|
6. |
|
|
|
|
7. |
|
|
|
|
8. |
|
|
|
|
9. |
|
|
|
|
10. |
|
|
|
|
11. |
|
|
|
|
12. |
|
|
|
|
13. |
|
|
|
|
14. |
|
|
|
|
15. |
|
|
|
|
16. |
|
|
|
|
17. |
|
|
|
|
18. |
|
|
|
|
19. |
|
|
|
|
20. |
|
|
|
|
21. |
|
|
|
|
22. |
|
|
|
|
23. |
|
|
|
|
24. |
|
|
|
|
25. |
|
|
|
ЗАДАНИЕ 6
Найти экстремум функции двух
переменных:
|
1. |
Z
= 2x3+xy+y2/2+5y |
14. |
Z
= x2+xy+y2-2x+3y- |
|
2. |
Z =
x2-xy+y3+2x-y |
15. |
Z =
x3+4xy+2y2+4y |
|
3. |
Z
= x2+xy+3y2+16x |
16. |
Z
= x2+2xy+y3+8x |
|
4. |
Z
= x3+2xy+y2+5y-3x+18 |
17. |
Z
= 2x2+3xy+y3+x |
|
5. |
Z
= x2-xy+y3-5x |
18. |
Z
= x2+3xy+y3-x |
|
6. |
Z
= x3+4xy+2y2+4y |
19. |
Z = x2+2xy+y3+8x |
|
7. |
Z
= 2x2+2xy+y3+4x |
20. |
Z
= x2-4xy+y3+4x |
|
8. |
Z
= 2x3+xy+0,5y2+y |
21. |
Z = x3+xy+3y2+16y |
|
9. |
Z
= x3+3xy+3y2+12y |
22. |
Z
= x3-5xy+2y2+2y |
|
10. |
Z
= x3+2xy+2y2+10y |
23. |
Z
= x2+xy+y3+4x |
|
11. |
Z =
x3+xy+2y2+2y |
24. |
Z
= x2+xy+3y3+4x |
|
12. |
Z
= x2 +2xy+y3+16x |
25. |
Z
= x3+xy+3y2+4y |
|
13. |
Z
= x3+3xy+3y2+9y |
|
|
ЗАДАНИЕ 7
Решить систему методом Гаусса.
1.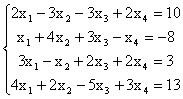 2.
2. 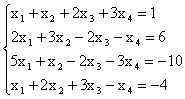
3. 4.
4.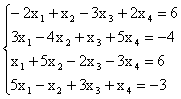
5. 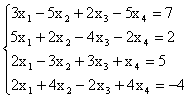 6.
6. 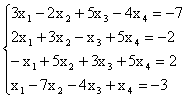
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 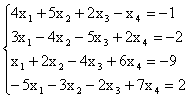
13. 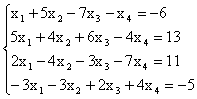 14.
14. 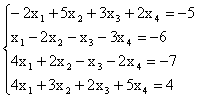
15. 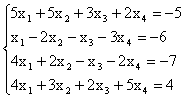 16.
16. 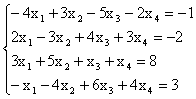
17. 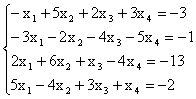 18.
18. 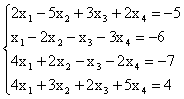
19. 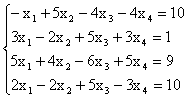 20.
20. 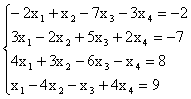
21. 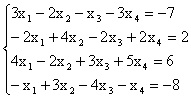 22.
22. 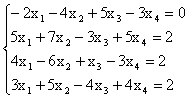
23.  24.
24. 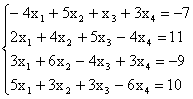
25. 
ЗАДАНИЕ 8
Даны векторы а1, а2 а3 а4. Показать, что векторы а1 , а2 , а3,, а4. образуют базис трехмерного пространства. Найти координаты вектора в в этом базисе. (Систему решить матричным методом и методом Крамера.)
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]()
13. ![]()
14. ![]()
15. ![]()
16. ![]()
17. ![]()
18. ![]()
19. ![]()
20. ![]()
21. ![]()
22. ![]()
23. ![]()
24. ![]()
25. ![]()
ЗАДАНИЕ 9
Найти частное решение дифференциального уравнения
у¢(1 + bх) = ay,
удовлетворяющего начальным условиям х0 =
0, у0 = 1. Написать три члена разложения в ряд частного решения
дифференциального уравнения. Вычислить приближенно и точно у1 = Q(x1). Сравнить результаты.
|
NN п/п |
а |
b |
x1 |
|
1 |
1 |
½ |
1 |
|
2 |
2 |
1 |
0,5 |
|
3 |
3 |
-1/2 |
1 |
|
4 |
-1 |
-1 |
0,5 |
|
5 |
-2 |
1/2 |
1 |
|
6 |
-3 |
1 |
0,5 |
|
7 |
1/2 |
1 |
0,25 |
|
8 |
1/3 |
1 |
0,331 |
|
9 |
-1/2 |
1 |
0,25 |
|
10 |
-1/3 |
1 |
0,331 |
|
11 |
1 |
1 |
0,5 |
|
12 |
2 |
1/2 |
1 |
|
13 |
-2 |
1 |
0,25 |
|
14 |
-1 |
1/3 |
2 |
|
15 |
1,5 |
1 |
1/3 |
|
16 |
-1,5 |
1 |
0,5 |
|
17 |
2,5 |
1 |
0,25 |
|
18 |
-2,5 |
1 |
0,1 |
|
19 |
1 |
1/3 |
0,2 |
|
20 |
2 |
-1/2 |
0,25 |
|
21 |
-1 |
-1/3 |
0,5 |
|
22 |
-2 |
-1/2 |
0,2 |
|
23 |
1 |
-1 |
0,1 |
|
24 |
3 |
-1 |
-0,25 |
|
25 |
2 |
-1 |
-0,2 |
Учебное издание
Высшая математика
Методические указания и контрольные задания
(для студентов экономических специальностей заочной формы обучения)
Составители Зима
Нина Евтихиевна
Медведева Марина Ивановна
Миронова Елена Михайловна
Новожилова Елена Геннадиевна
Николайчук Галина Михайловна
Онюшкина
Алла Васильевна
Редактор Л.Х. Соловьева
СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ
1. Данко П.Е., Попова А.Г.
Высшая математика в упражнениях и задачах. -М.: Высш.шк., 1974.-Ч. 1.-346 с.
2. Ильин В.А., Поздняков Э.Г. Линейная алгебра. -М.: Наука, 1974.-302 с.
3. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. -М.: Высш. шк., 1982.-Ч.1.-272 с.
4. Кудрявцев В.А., Демидович
В.П. Краткий курс математики. -М.: Наука,1975.-622 с.
5. Минорский В.П. Сборник задач по высшей математики. -М.: Наука, 1977.-352 с.