§ 2. Операции над событиями. Алгебры и

s - алгебры событий

Пространство элементарных исходов может иметь довольно сложную структуру.

Пример 2.1. Рассмотрим случайный эксперимент, состоящий в том, что два игрока поочередно подбрасывают симметричную монету до тех пор пока не выпадет герб.

Что следует назвать элементарным исходом такого эксперимента? Пусть литера Г означает появление герба, литера Р - появление решки. Тогда элементарный исход нашего воображаемого эксперимента можно изобразить в виде бесконечной последовательности литер Г и Р, например,

w = ( Р Р ... Р Г ).

Если сопоставить литере Р цифру 0, а литере Г цифру 1, то каждому элементарному исходу w ставится во взамно-однозначное соответствие число, заданное своим двоичным разложением

w « 0,00...01.

Поскольку каждое вещественное число из отрезка [0,1] можно представить в виде его двоичной записи, то пространство элементарных исходов можно отождествить с отрезком [0,1] : W = [0,1] .

Далее, так как игроки продолжают подбрасывание до тех пор, пока не выпадет герб. Обозначим А событие “ выиграл первый игрок (бросавший первым)” .

Событию А следует сопоставить подмножество чисел из отрезка [0,1] таких, что цифра 1 появиться в них впервые на нечетном после запятой месте:

А ={0,1 ...; 0,001 ... ; 0,00001 ...; ... }.

Как назначить разумным образом вероятности элементарных исходов в рассматриваемом эксперименте?

Поскольку, если первый игрок выигрывает при бросании с номером 2k+1, дальнейшее продолжение игры теряет смысл, то разумно принять следующие вероятности

Р(первый игрок выигрывает при бросании с номером 2к+1) =

(всего имеется 22k+1 возможных исходов, один из них благоприятен).

Теперь, согласно определению 1.1

.

Обозначим В событие “выиграл второй игрок”.

Подобно вышеизложенному, событию В ставим в соответствие подмножество из отрезка [0,1] , состоящее из чисел, в которых 1 появится впервые на четном месте:

В ={0,01 ...; 0,0001 ... ; 0,000001 ...; ... }.

Аналогичные соображения приводят к равенству

Р(второй игрок выигрывает при бросании с номером 2к) = ,

и к равенству

 

. u

 

Мы уже условились отождествлять со случайным событием некоторое подмножество пространства элементарных исходов W.Ё

Определение 2.1. Достоверным событием называют событие, происходящее при всяком осуществлении случайного эксперимента.

Невозможным событием называют событие, которое в условиях эксперимента не происходит никогда.

 

Достоверному событию благоприятствует любой элементарный исход, поэтому его обозначают той же литерой, что и пространство элементарных исходов, W. Невозможному событию не благоприятствует ни один элементарный исход, его обозначают символом пустого множества, Ж.

 

Определение 2.2. Событие А влечет за собой событие В, если событие В происходит всякий раз, когда происходит А . Обозначение: А М В.

 

По определению, Ж М А. для любого события А.

События А и В эквивалентны (равны), если одновременно верны два соотношения А М В и В М А. В этом случае пишут А = В.

Очевидно, А М W , каково бы ни было А.

 

Определение 2.3. Пусть имеем события А и В. Их суммой (объединением) называют событие С , происходящее тогда и только тогда, когда происходит хотя бы одно из данных событий, при этом пишут С = А И В.

Верны равенства А И W = W , А И Ж = А, каково бы ни было А.

Определение 2.4. Пусть имеем события А и В. Их произведением (пересечением) называют событие С , происходящее тогда и только тогда, когда происходят одновременно оба данных события, при этом пишут

С = А З В.

Верно всегда А З W = A , А З Ж = Ж для любого события А.

Введенные выше понятия принято иллюстрировать с помощью так называемых диаграмм Венна, изображая пространство элементарных исходов W внутренностью квадрата, а события - его подмножествами.

 

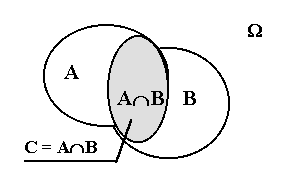
Рис. 2.1 Рис. 2.2 Рис. 2.3

На рисунках 2.1 - 2.3 изображены диаграммы Венна, соответствующие понятиям А М В, А И В, А З В соответственно.

Определение 2.5. События А и В называются несовместными, если

А З В = Ж (одновременное их осуществление невозможно).

Соответствующая диаграмма Венна имеет вид:

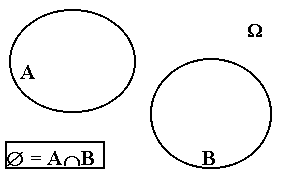
Рис. 2.4

Определение 2.6. Событие называются противоположным событию А, если оно происходит тогда и только тогда, когда А не происходит.

На диаграмме изображается внешностью подмножества А:

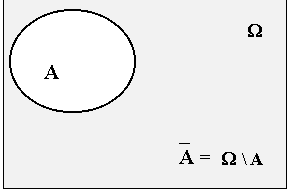
Рис. 2.5

Очевидно, что два события являются противоположными, если

Тогда = В.

Определение 2.6. Разностью событий А и В (в указанном порядке) называют событие С, происходящее тогда и только тогда, когда происходит событие А и , при этом пишут С = А\ В = А З .

Аналогично определяют В \ А. Диаграмма Венна имеет вид:

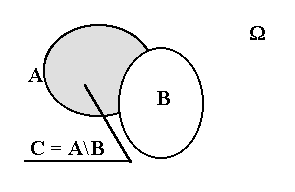
Рис. 2.6

Полезны следующие равенства:

(формулы двойственности).

Докажем, например, последнее из них.

Пусть произошло событие . Это значит, что не произошло событие

A З B, то есть, произошло либо событие А, а событие В не произошло, либо произошло событие В, а событие А нет. В любом случае произошло либо , либо , то есть произошло событие .

Итак, .

Пусть теперь произошло событие , то есть произошло хотя бы одно из событий либо , то есть либо А, либо В (либо оба) не произошло, а следовательно, не произошло событие BЗA, но тогда произошло .

Итак, всегда .

В силу определения 2.2 получаем .

 

Пример 2.2. Игральная кость подбрасывается один раз. Обозначим wi элементарный исход, означающий появление грани, на которой i - очков (i = 1,2,3,4,5,6).

Тогда W = { w1, w2 , w3, w4, w5, w6 }.

Пусть событие А - “на верхней грани четное число очков”.

Событие В - “ на верхней грани число очков, кратное трем”.

Тогда А = { w2, w4 , w6 }, В = { w3, w6 }.

Рассмотрим события:

а) С = А ИВ = { w2 , w3, w4, w6 } - на верхней грани число очков не менее двух, но не пять;

б) D = А З В = { w6 } - состоит в том, что выпала грань с числом очков шесть;

в) Е = А \ В = { w2, w4 } - на верхней грани четное число очков, но не шесть;

г) Н = В \ А = { w3 } - на верхней грани три очка ;

д) F = = { w1, w3, w5 } - выпала нечетное число очков;

е) G = = { w1, w2, w4 , w5 } - число очков на верхней грани не делится на три;

ж) = = { w1, w5 } - число очков на верхней грани нечетно и не равно трём. u

Понятие суммы и произведения переносятся на бесконечные наборы событий.

С = А1 И А2И А3И ... И АnИ ...=

происходит тогда и только тогда, когда происходит хотя бы одно из событий А1 , А2, ... .

Событие

D = А1 З А2 З А3 З ... З Аn З ...=

происходит тогда и только тогда, когда происходят одновременно все события А1 , А2, ... .

 

Оказывается, что для корректного определения вероятности как функции от события следует накладывать некоторые условия на область определения.

Пусть W - пространство элементарных событий, а Б - некоторый класс случайных событий (подмножеств W ).

Определение А1. Класс Б называют алгеброй событий, если:

1) W О Б ;

2) А О Б Ю О Б ;

3) А ,В О Б Ю А ИВ О Б .

Из определения А1 заключаем, что в любой алгебре Ж О Б ; из того, что А и В О Б следует, что А З В , А \ В , В \ А О Б .

Пример 2.3. Построим Б - алгебру событий в примере 2.2.

В неё входит невозможное событие Ж и достоверное событие W, все элементарные события { w1 },{w2 },{ w3},{w4 },{ w5},{w6},

все события вида { w1 , w2 }, ..., { w2 , w3}, ... , все события вида { w1 , w2 , w3},

{ w3,w4 , w5}, ... , все события вида { w3,w4 , w5, w6 },..., и так далее - всего 26 = =64 события. u

Определение А2. Алгебра событий Б называется s - алгеброй (сигма - алгеброй), если вместо аксиомы 3) имеет место аксиома

3/ ) Аn О Б , (n = 1,2,3, ... ) Ю О Б .

Из формул двойственности следует, что в сигма алгебре для каждой последовательности событий Аn О Б , (n = 1,2,3, ... ) их пересечение

О Б

Определение Р . Пусть имеем пространство элементарных исходов W и s - алгебру событий Б . Функция Р(о ) с областью определения Б называется вероятностью, если она удовлетворяет условиям:

Р1. Р(А) і 0, для любого события А из Б ;

Р2. Р( W) = 1;

Р3. ,

если А1 , А2, ..., Аn , ... О Б , Аi З Вj =Ж ().

Доказывается, что любой убывающей последовательности событий из Б

А1 Й А2 Й А3 Й ... Й Аn Й ... и такой, что = Ж

имеет место равенство P( Аn ) = 0 (непрерывность вероятности).

 

Тройка объектов {W, Б , Р} называется вероятностным пространством.

4 В оглавление ÷ Назад Дальше ø