1. М н о ж е с
т в а
Понятия
множества и элемента множества являются первичными понятиями. Теория множеств как
математическая дисциплина создана немецким математиком, Георгом Кантором в
В первом издании “Теории множеств” Бурбаки (1939г.) имеется следующее предложение: « Множество образуется из элементов, обладающих некоторыми свойствами и находящихся в некоторых отношениях между собой или с элементами других множеств ».
Первичным понятием является также понятие пустого множества. Пустое множество не содержит элементов. Объекты, сущности или элементы, составляющие множество, обозначаются строчными латинскими буквами: х, а, b, ...; множество будем обозначать прописными латинскими буквами Е, N, ... . Знак Î обозначает вхождение или принадлежность.
Под множеством А = {a,b,c,...} понимается собрание (совокупность) некоторых элементов а,b,c,... . Если х есть элемент множества А, то пишут
х ![]() А
А
(читается: х принадлежит А); если у не является элементом множества А, то пишут
y ![]() А
А
(читается: у не принадлежит множеству А).
2. Способы
задания множеств
а) Множество может быть задано перечислением всех его элементов.
П р и м е р ы :
1. Множество цифр: А = {0,1,2,...,9};
2. Множество лиц, присутствующих на собрании:
В = {Иванов, Сидоров, Петров, Павлов}
b) Обобщение первого способа состоит в том, что каждый элемент задаваемого множества определяется по некоторому элементу уже известного множества.
П р и м е р ы : считая известным множество действительных чисел
Z = {... -3,-2,-1,0,1,2,3,...},
определим множество степеней числа 10
D = {..., 10-3, 10-2,10-1,100, 101,102,103,...}
c) Другой способ состоит в описании ограничительного свойства, выделяющего элементы множества из другого более широкого или основного множества.
П р и м е р ы : 1. Считая известным множество натуральных чисел
N = {1,2,3,4,...},
определим множество четных чисел
L = {2,4,6,..., 2n+2, ...}, где n ÎN.
2. [а,b] = {х: а ![]() х
х ![]() b} - отрезок;
b} - отрезок;
3. B - множество деревьев в парке;
4. Множество трехголовых людей пусто, т.е. оно
не содержит ни одного элемента
(обозначать это множество будем ![]() ).
).
d) Новые множества можно задавать при помощи некоторых операций над множествами.
3.
Операции над множествами

(читается: множество А содержится во множестве В либо равно В).
Условимся считать, что пустое множество есть подмножество любого множества.
![]() Будем
изображать, для наглядности, множества при помощи диаграммы Эйлера-Венна, изображающие эти множества и наглядно
демонстрируют некоторые свойства операций над множествами.
Будем
изображать, для наглядности, множества при помощи диаграммы Эйлера-Венна, изображающие эти множества и наглядно
демонстрируют некоторые свойства операций над множествами.
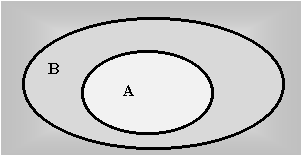
Если
![]() а
а ![]() В
В ![]() а
а ![]() А,
А,
тогда А = В.
 Рис.3.1.
Рис.3.1.
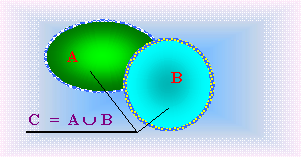
Рис. 3.2.
Аналогично определяется объединение большего числа множеств.
П р
и м е р : {1,2,3} ![]() {2,3,4} = {1,2,3,4}.
{2,3,4} = {1,2,3,4}.

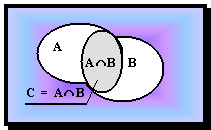
Рис. 3.3
Если
множества А и В не имеют общих элементов, то их пересечение пусто:
А ![]() В =
В = ![]() .
.
Аналогично определяется пересечение большего числа множеств.
П р
и м е р :
{1,2,3} ![]() {2,3,4} = {2,3} = С.
{2,3,4} = {2,3} = С.

(С = В \ А - аналогично).
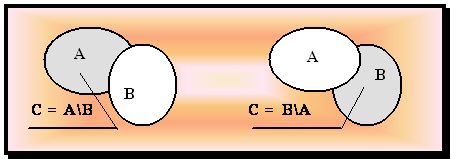
Рис. 3.4.
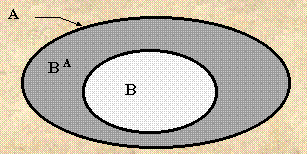
Если ![]() , то множество
, то множество![]() ВА = А\ В
называется дополнением
ВА = А\ В
называется дополнением ![]() множества В до множества А.
множества В до множества А.
Очевидно,
В![]() ВА = A,
ВА = A,
В ![]() ВА =
ВА = ![]() .
.
Рис. 3.5.![]()
Кратко эти определения можно записать следующим
образом:
А
![]() В = {x: x - принадлежит по крайней мере одному из
множеств
В = {x: x - принадлежит по крайней мере одному из
множеств![]() А или В};
А или В};
А
![]() В = {x: x
В = {x: x ![]() А и x
А и x![]() В};
В};
А
\ В = {x: x ![]() А и x
А и x ![]() В}.
В}.
Если
задана система множеств {Ai} (i=1¸n), то их объединение ![]() и пересечение
и пересечение ![]() , определяются соответственно по формулам:
, определяются соответственно по формулам:
![]() = {x: x - принадлежит по крайней мере одному из
множеств А};
= {x: x - принадлежит по крайней мере одному из
множеств А};
![]() = {x: x
= {x: x ![]() Аi,
Аi, ![]() i=1¸n }.
i=1¸n }.