Глава I

 

Элементы аналитической геометрии

 

1.  Прямоугольные координаты точки на плоскости

 

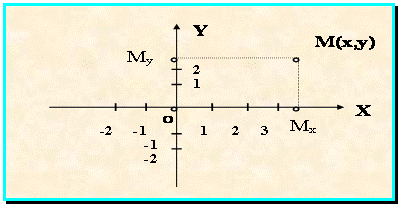
            Положение точки на плоскости проще всего определить при помощи прямоугольной системы координат (декартовы координаты), которую мы определим следующим образом:

 

            1) выберем две взаимно перпендикулярные прямые - две оси координат (ось абсцисс и ось ординат), точка их пересечения называется начало координат (обозначим буквой O);

            2) на каждой оси выберем положительное направление;

 

Рис. 1.1.

            3) для каждой оси выберем единицу длины.

 

 

            Положение точки  М  относительно выбранной системы координат определяется двумя координатами - абсциссой  х  (число,  равное длине oмх) и ординатой  у  (длина oму).     Эти два числа полностью определяют положение точки на плоскости.

 

 

            Отрезок, соединяющий начало координат с точкой М,  называется ее радиусом-вектором.

 

Рис.  1.2.

 

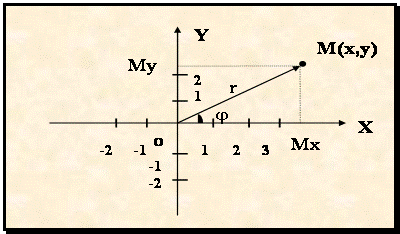
            Обозначим через  j  угол, образованный  ОМ  с положительным направлением оси  Ох,  и через   r - его длину, тогда можно координаты точки определить следующим образом:

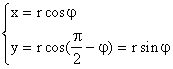
(1.1)

 

 

 

 

 

 

 

При решении различного рода задач, иногда выгодно, вместо данной системы координат Оху, решать задачу в другой системе координат и тогда возникает вопрос о переходе от одной системы координат к другой и обратно. Другими словами, выбирается система координат О'х'у', определенным образом ориентированная относительно первой Оху.

Рассмотрим простейший случай, когда происходит простой параллельный перенос системы координат.

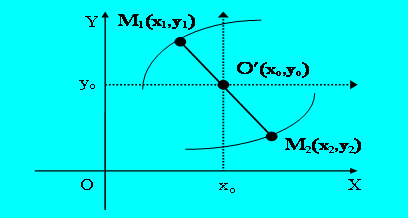
            Пусть начало новой системы координат О'х'у', по отношению к старой имеет координаты О'(а,b). Возьмем произвольную точку М(х,у) в старой системе координат, которая в новой системе будет иметь некоторые «новые координаты» (х'у') (См. рис.1.2.1).

 

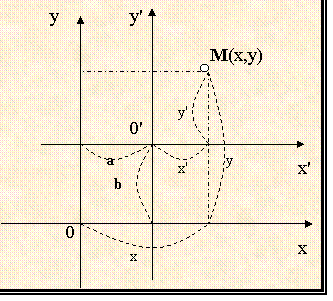
Тогда получаем, что

х' = х – а,

  у' = у – b    

      (1.1.1)

т.е. новые координаты точки М(х'у') равны ее старым координатам минус координаты нового начала.

Обратно, из (1.1.1) находим

 х = х' + а,

                                  у = у'+ b.                (1.1.2)

Рис.1.2.1

 

Теперь рассмотрим поворот «новой системы» координат О'х'у' относительно «старой системы» Оху на некоторый угол a (рис.1.2.2), т.е. Ðх¢Ох = a считается положительным, если поворот осуществляется против 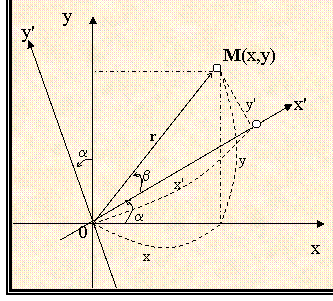часовой стрелки и отрицательный в противном случае.

Пусть угол b - угол между радиус-вектором точки М (r = OM) и осью Ох¢ ; тогда r, с учетом знака угла b, будет составлять с осью Ох угол

a +b. Тогда на основании формул (1.1) при любом расположении точки М имеем

 

.

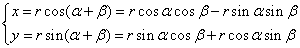А так как новые координаты точки М есть

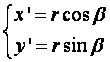,                  (1.1.3)

то тогда можно вернуться к старым координатам

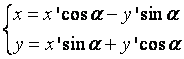.                       (1.1.4)

 

Теперь, если рассмотреть общий случай, когда новое начало координат есть точка О'(а,b) и ось О'х' образует с осью Ох угол a, то на основании формул (1.1.1) и (1.1.4) имеем

 

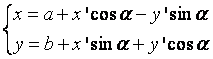.            (1.1.5)

           

При повороте системы относительно данной на угол -a, необходимо принять во внимание, что cos(-a) = cosa, sin(-a) = -sin(a), будем, соответственно иметь

 

,    .

 

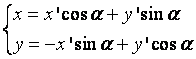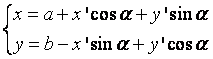1.2. Расстояние между двумя точками на плоскости

 

            Найдем сначала длину r-вектора, т.е. это будет расстояние точки  М(х,у) от начала координат О(о,о). Расстояние  r = ОМ, очевидно, является гипотенузой прямоугольного треугольника ОММх с катетами ОМх = ç х ç и ММх = ç у ê. По теореме Пифагора получаем

                                                                   r =                                                          (1.2)

     В общем случае, пусть даны две точки А(х1,у1) и В(х2,у2) и требуется найти расстояние между ними (r(А,В))

 

 

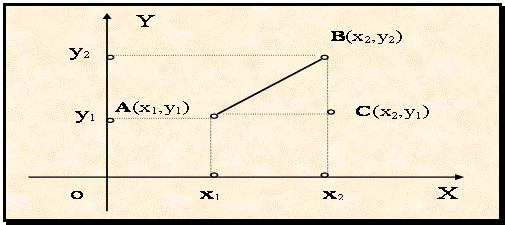
Рис. 1.3.

 

            Так как длина АС =  çх2 - x1ç, а ВС = çу2 - у1ç, тогда, используя (1.2), получаем

 

                                  r(A,B) =                                                            (1.3)

 

З а м е ч а н и е .  Формула (1.3) дает возможность найти и длину отрезка АВ. 

 

1.3. Линия как множество точек

 

            Изучение свойств геометрических фигур с помощью алгебры  носит название аналитической геометрии, а использовать при этом мы будем так называемый метод координат.

            Линия на плоскости обычно задается как множество точек, которые обладают присущими только им свойствами. Тот факт, что координаты (числа)  х  и  у точки, лежащей на этой линии, аналитически записываются в виде некоторого уравнения.

 

Определение 1.1.  Уравнением линии (уравнением кривой) на плоскости  Оху    называется уравнение, которому удовлетворяют   координаты  х  и  у  каждой точки данной линии и не   удовлетворяют координаты любой другой точки, не    лежащей на этой линии.

 

            Из определения 1.1  следует, что всякой линии на плоскости соответствует некоторое уравнение между текущими координатами (х,у) точки этой линии и наоборот, всякому уравнению соответствует, вообще говоря, некоторая линия.

            Отсюда возникают две основные задачи аналитической геометрии на плоскости.

            ˆ  -    Дана линия в виде множества точек. Нужно составить уравнение

                      этой линии.

            ˆ  -    Дано уравнение линии. Необходимо изучить ее геометрические

                      свойства (форму и расположение).

1.4. Прямые в  R2

 

            Пусть задана декартова система координат  Оху  и через произвольную точку М(х,у) проведена прямая линия   .  Теперь пусть эта прямая, для определенности, образует угол  j (0 £ j £ )  с положительным направлением оси  Ох.  Тогда прямая пересекает ось ординат в некоторой точке  В(0, b), а ордината текущей точки  М(х,у)  равна NМ,  т.е.  у = NМ = NC + СМ, где NC=b  есть величина постоянная для данной прямой, а вторая переменная и  СМ = ВС tg j = kx.

 

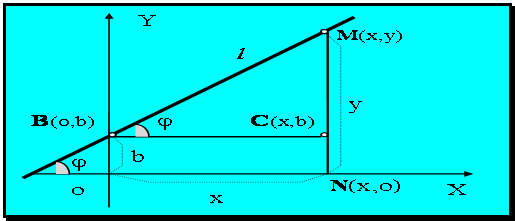
Рис. 1.4.

 

 

 

Таким образом,

                                                            y = kx + b                                                                       (1.4)

 

при х  ³  0. (Проверьте самостоятельно справедливостьформулы (1.4) для  х < 0.). Так как координаты  точки  М(х,у) Î , то они удовлетворяют уравнению (1.4).

            Убедитесь в обратном. Пусть координаты  точки М(х1,у1) удовлетворяют уравнению (1.4), то точка обязательно лежит на прямой. Следовательно, уравнение (1.4) представляет собой уравнение прямой линии с угловым коэффициентом, где k и  b - параметры, имеющие следующие значения: b - отрезок, который отсекает прямая от начала координат до точки пересечения прямой с осью Оу;   k = tg j  - угловой коэффициент.

 

            Самостоятельно рассмотреть:  b < 0,  b > 0, b = 0;   j = 0,   p/2 < j < p,  j  = p/2.

 

Теорема 1.1.  Всякое невырожденное уравнение первой степени

                                             Ах + Ву + С = 0          (А2 + В2 ¹ 0)                                             (1.5)

 представляет собой общее уравнение прямой на плоскости  Оху.

 

Д о к а з а т е л ь с т в о:  1).  Пусть В ¹ 0.  Тогда уравнение (1.5) запишем в каноническом виде                                               

сравним с  (1.4), получим  k = - А/В;  b = -C/B.

2).  Пусть теперь  В = 0,  а  А ¹ 0,  имеем  Ах + С = 0  и х = -С/А,              (1.6)

получаем прямую параллельную оси  Оу.

 

1.4.1. Взаимное расположение двух прямых в R2

 

     Пусть заданы две прямые

                                                      l2:   у = k2x + b2,   где  k2 =  tg  a,

                               и

                                           l1:   у = k1x + b1,   где  k1 = tg j .

Очевидно, что взаимное расположение этих прямых можно определить

при помощи  Ð b . (См. Рис. 1.5).

 

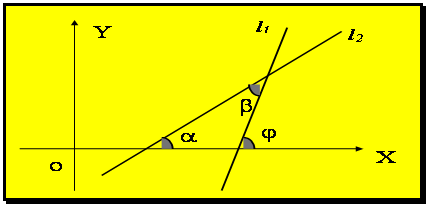
Рис. 1.5.

 

            Из элементарной геометрии известно, что внешний угол j = a + b или

b = j - a. Отсюда на основании

 

              .                                           (1.7)

 

На основании формулы (1.7) получим условия параллельности и перпендикулярности двух прямых:

1.  Если  k2 = k1, то прямые параллельны, т.к.  a = j,   а  b = 0.

2.  Если  k2= - 1/k1.

 

З а м е ч а н и е.  Пусть заданы две прямые

                             (1):  Ах + Ву + С = 0

                             (2): А1х + В1у + С1 = 0,  тогда

                                         

                                          

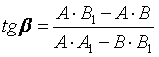
            1).  (1) çç(2) Þ    - условие параллельности двух прямых;

 

            2).  (1) ^ (2) Þ  AA1 + BB1  = 0 - условие перпендикулярности двух прямых.

Дополнения к прямой на плоскости

 

2. Линии второго порядка

2.1. Окружность

 

            Пусть задана точка С(хо,уо) и R - радиус. Тогда, если для  любой точки М(х,у) справедливо  |MС|=R, то линия называется окружностью.

            Уравнение получается из того, что

                                             r(М,С) = = R,

 и называется нормальным уравнением окружности, т.е.

                                                  .                                                        (2.1)

 

 

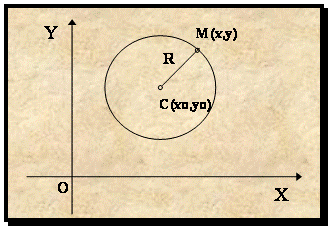
Рис. 2.1.

 

            В частном случае xо = 0,  уо = 0 :

                                                                          х2 + у2 =R2                                                         (2.2)

            Уравнение (2.1) можно записать в виде:

                                                                x2 + y2 + A×x + B×y + C = 0,                                          (2.3)

т.е. окружность является кривой второго порядка.

 

Определение 2.1. Линия называется линией (или кривой) nго порядка (n = 1,2, ...), если  она определяется уравнением  nй  -  степени  относительно  текущих  прямоугольных   координат.

 

            Тогда общий вид кривых первого порядка есть

                                                           Ах + Ву + С = 0,                                                                  (2.4)

где А и В  ¹ 0 одновременно.

            Соответственно

                                               Ax2 + By2 + Cx + Dy + F = 0,                                                           (2.5)

 где  A2 + B2 + C2 ¹ 0.  Тогда (2.5)- общий вид кривых второго порядка.

 

З а м е ч а н и е. Не всякому уравнению второго порядка соответствует действительная кривая.

 

Пример. Пусть задано уравнение второго порядка  x2 + 2xy + y2 + 1 = 0,

            Так как  нет действительных чисел x, y, что удовлетворяют этому уравнению, то не существует и

 действительной кривой.

 

Таким образом,     Ax2 + Ay2 + Dx + Ey + F = 0  является общим уравнением окружности.

 

            Если  A ¹ 0 , тогда разделим почленно, получим

что соответствует (2.3).

           

Тогда для того , чтобы действительная кривая второго порядка являлась окружностью,  необходимо:

                          1. Равенство коэффициенты при квадратах текущих координат;

                          2. Отсутствие члена, содержащего произведение текущих координат.

 

2.2. Центральные кривые второго порядка

 

            Рассмотрим  уравнение

Ax2 + Cy2 + Dx + Ey + F = 0

(A ¹ 0, C ¹ 0, без члена, содержащего х,у).

 

            Выделим в этом уравнении полный квадрат

                                     A ( x+ )2 + C ( y + )2  =   +   -  F.                               (2.6)

             Теперь положим

xo = -,     yo = -,  D = +- F .

Получим

                                          A(x - xo)2 + C(y - yo)2  = D.                                                                    (2.7)

 

 

Точку  O/ (xo,yo) назовем точкой симметрии кривой (2.7) (центром кривой).

Т.е. если точка  M1 (x1,y1) Î l  точка M2(x2,y2), симметричная относительно O/, очеви-дно также лежит на  l (2.7).

            Параллельные осям координат Ох и Оу прямые  y = yo, x = xo  являются осями симметрии кривой (2.7).

 

 

 

 

 

                                                                                                                                                          Рис.2.2.

 

Для простоты положим, что  O/(0,0) находится в начале координат. Тогда (2.7) принимает вид : 

                                         

Ax2  + Cy2 = D.                                                   (2.8)

 

2.3. Кривые эллиптического и гиперболического типа

 

Определение 2.2. Кривая второго порядка (2.8) называется эллипсом (принадлежит эллиптическому типу), если коэффициенты А и С имеют одинаковые знаки, т.е.             

А×С > 0                                                                  (2.9)

            Пусть для определенности A > 0, C > 0

1). D > 0  тогда  будем иметь действительный эллипс;

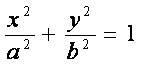                                               , (каноническое уравнение)                (2.10)

            где

                                               .

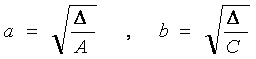 Числа a, b называются полуосями эллипса. Обычно полагают 0 < b £ a .

 

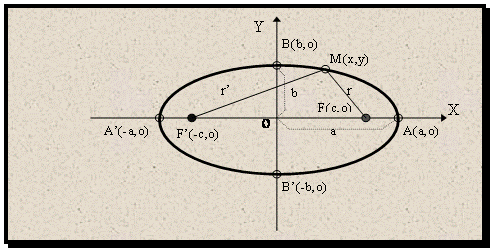
Рис.2.3.

 

Точки   A’, B’ A, B - называются вершинами эллипса,

              AA/ = 2a, BB’= 2b- называются его осями.

Отметим, что  ½x½ £ a, ½y½£ b , если  a = b и, тогда x2 + y2 = a2  -  окружность.

2). Если D = 0,  то O(0,0) - вырожденный эллипс.

3). При D< 0  (2.8)  не имеет действительных точек и эллипс называется мнимым эллипсом.

 

Определение 2.3. Кривая второго порядка (2.8) называется гиперболой (кривой гиперболического типа), если А и С имеют противоположные знаки, т.е.

                                                                 АC < 0                                                                      (2.11)

Пусть А > 0, С > 0.

1. D > 0 - имеем гиперболу с каноническим уравнением

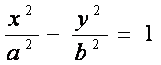                                                         ,                                                  (2.12)

где 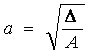 - действительная полуось, 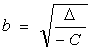   - мнимая полуось.

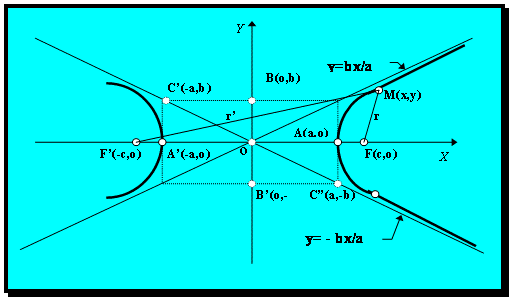
 Точки A/ (-a,o), A(a,o) - вершины гиперболы.

Отметим, что здесь  ½x½ ³ a .

2. D = 0 - будет пара пересекающихся прямых (вырожденная гипербола)

.

 

 

Рис.2.5.

 

 

 

            3. D < 0  получим гиперболу с полуосями

a/ =  и   b/=.

 

 

 

 

Если a/ = a   и   b/ = b  , то гипербола

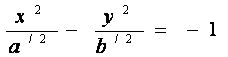                                                                                              (2.13)

 

называется сопряженной к гиперболе (2.12) и ее вершинами будут точки В(o,b)   и   B/ (o,-b).  

Отрезок AA/ = 2а - действительная ось;   BB/ = 2b - мнимая ось гиперболы.

 

2.4. Фокальные свойства центральных кривых второго порядка

 

Точки F(c,0) и F/(-c,0) называются фокусами,

 где      c=   (“+” - для гиперболы;“-”  - для эллипса).                                       (2.14)

Отношение e =  называется эксцентриситетом центральной кривой второго порядка:

                                   1) для эллипса 0 £ e < 1;

                                   2) для гиперболы 1< e < ¥ :

                                   3) для окружности e = 0.

            Пусть имеем точку M(x,y). Обозначим r = MF и r/ = MF/ (r,r/ - фокальные радиусы). Тогда имеем   

 

  и  .

Так как

 

  откуда   , с учетом (2.14)  получим, что

 

r = 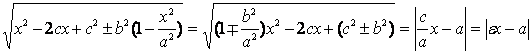 .    (2.15)

 

Аналогично(самостоятельно):

                                            r/ = 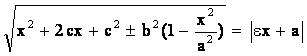                     (2.16)

Тогда получаем:

1). Если кривая эллипс, то  0  £  e  <  1 ,    çx ç £  a

поэтому  r = a - ex,   r/  = a + ex

получим, что                                r + r/ = 2a                                                                           (2.17)

 

  Для каждой точки М(х,у), принадлежащей эллипсу, сумма ее фокальных радиусов есть величина постоянная (характеристическое свойство эллипса).

2). Для гиперболы e > 1, çx ç  ³   a

r = ± (ex -  a),         r/ = ± (ex + a) .

            “+” соответствует правой ветви гиперболы (х>0);

             “-” соответствует левой ветви (х<0).

                                                                                  r/ - r = ± 2a                                              (2.18)

(характеристическое свойство).

            Для каждой точки М(х,у), принадлежащей гиперболе, абсолютная величина разности ее фокальных радиусов есть величина постоянная.

 

2.5. Асимптоты гиперболы

 

Рассмотрим

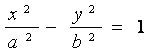                     или

.

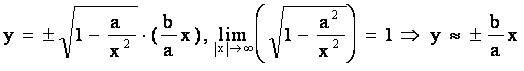Тогда  y =   - называется асимптотой гиперболы.

Пусть, например, х>0. Рассмотрим точки M(x,y),  принадлежащую  гиперболе и    N(x,y/)- прямой, тогда

 

 .

 

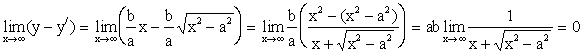З а м е ч а н и е. Для равнобокой гиперболы (а = b)

x2 - y2 = a2

асимптоты y = ±x  взаимно перпендикулярны.

 

2.6. Нецентральные кривые второго порядка

 

            Если кривая второго порядка не имеет центра симметрии, то она называется нецентральной.

           

Пусть                                Ax2 + Cy2 + Dx + Еy + F = 0,

 

где  A = 0, C ¹ 0, D ¹ 0.

           

Дополним в этом уравнении члены при у до полного квадрата

или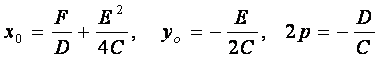

                                      (2.19)

            Кривая (2.19) называется параболой.

O/(xo,yo) - вершина параболы,  р - параметр параболы,    y = yo - ось симметрии параболы (ось параболы).

Пусть вершина параболы находится в O/(0,0) тогда кривая имеет вид:

 

 

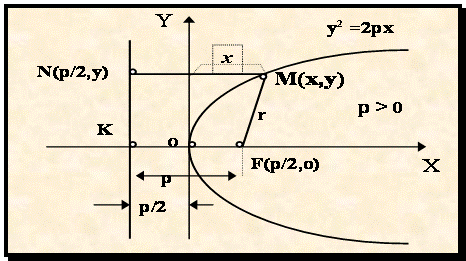
Рис.2.6.

 

2.7. Фокальное свойство параболы

 

y2 = 2px    (p>0).

            Точка F(p/2,0) называется ее фокусом; а прямая х = - р/2  - директрисой.

            Для точки M(x,y)  ее фокальный радиус   r = MF  и вычисляется

 

r =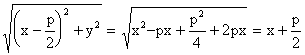

 

С другой стороны расстояние этой точки от директрисы равно

 

MN = x + p/2 = r.

 

Таким образом, получаем определение параболы:

 

Определение 2.4.  Парабола представляет собой множество точек плоскости, равноотстоящих от данной точки (фокуса) и от данной прямой (директрисы). (Это - характеристическое свойство).

 

Самостоятельно рассмотреть графики квадратного трехчлена

 

y = Ax2 + Bx + C.

 

Назад  Далее