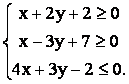Дополнения 1.
Прямая линия на плоскости
Если точка M(x; y; z) делит
отрезок между точками A(x1, y1, z1) и B(x2, y2, z2) в отношении l (т.е. |АМ|:|МВ| = l), то ее координаты находят по формулам
В частности, при делении отрезка пополам, т.е. при l = 1, получаем формулы для вычисления координат середины отрезка
Уравнением линии на плоскости Oxy называется уравнение,
которому удовлетворяют координаты (x, y) каждой точки данной линии
и не удовлетворяют координаты любой точки, не лежащей на этой линии. Всякое
уравнение первой степени относительно текущих координат x и y, т.е.
уравнение вида
Ax + By + C = 0,
где
A, B, C - постоянные коэффициенты, причем A2 + B2 ¹ 0 определяет на плоскости некоторую
прямую. Это уравнение называется общим
уравнением прямой.
Пример. Построить прямую 3x – 2y + 6 = 0.
Решение: Для построения прямой
достаточно знать какие-либо две ее точки, например, точки пересечения с осями
координат. Точку A пересечения прямой с
осью Оx можно получить, если в уравнении прямой принять y = 0.
Тогда имеем 3x + 6 = 0, т.е. x = -2. Таким образом, A(-2,
0). Аналогично, точка B - точка пересечения прямой
с осью Оy, имеет координату x = 0. Следовательно,
ордината точки B находится из уравнения –2y + 6 = 0, т.е. y = 3.
Значит, B(0, 3).
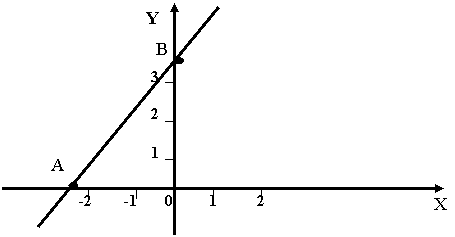
Если в общем уравнении
прямой B ¹ 0, то разрешив его относительно y,
получаем уравнение вида
y = k•x + b
(здесь k = - A/B, b =
-C/B). Его называют уравнением с угловым коэффициентом, т.к.
k = tga,
где a - угол, образованный прямой с
положительным направлением оси Ох.
Угловой коэффициент k прямой, заданной
двумя точками A(xA, yA) и
B(xB, yB),
где xA ¹ xB, можно вычислить по формуле
.
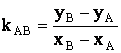Уравнение прямой, проходящей
через заданную точку A(xA, yA), с угловым коэффициентом k,
записывается в виде
y – yA = k(x - xA).
Рассмотрим
две прямые l1 и l1 (не параллельные оси Оy),
заданные уравнениями с угловыми коэффициентами. l1: y = k1x + b1 и l2: y = k2x + b2. Пусть j - угол между этими прямыми,
тогда
.
Условия
пересечения, параллельности, перпендикулярности
или совпадения двух прямых,
заданных общими уравнениями A1x + B1y +C1 = 0
и A2x + B2y +C2 = 0 имеют вид
1)
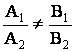(пересечение);
2)
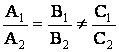(параллельность);
3)
А1А2 + В1В2 = 0
(перпендикулярность);
4)
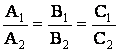(совпадение).
Если известны угловые
коэффициенты k1 и k2 прямых, то условия параллельности и перпендикулярности этих прямых имеют вид
k1 = k2 и k1 = -1/k2
соответственно.
Уравнение прямой, проходящей через две данные точки А(хА,уА)
и В(хВ,уВ), имеет вид
.
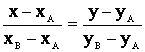Если прямая проходит через
точки А и В и параллельна оси Ох, т.е.
уА = уВ (или оси Оу, т.е. хА = хВ),
то уравнение такой прямой задается формулой у = уВ (х = хВ, соответственно).
Расстояние от точки М(х0,
у0) до прямой Ах + Ву
+ С = 0 находится по формуле
.
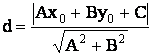Пример. Даны вершины треугольника А(2; -2), В(-4; 1), С(-1; 2). Сделать чертеж
и найти:
1) периметр треугольника;
2) уравнение высоты,
проведенной через вершину С;
3) уравнение прямой ЕС,
проходящей через точку С и параллельной прямой АВ;
4) уравнение медианы СМ,
проведенной через вершину С;
5) угол, который медиана ВМ1,
проведенная через вершину В, образует со стороной ВС;
6) координаты точки К -
пересечения медиан треугольника;
7) площадь треугольника АВС;
8) систему линейных неравенств,
определяющих треугольник АВС.
u Периметр треугольника РАВС равен
|AB| + |BC| + |CA|. Длины сторон найдем по
формуле расстояния между двумя точками. Имеем
,
,
.
Тогда PABC 
» 14,87.
v Найдем
уравнение высоты CD.
Так как CD
^ АВ, то по условию перпендикулярности
двух прямых kCD = -1/kAB.
Вычислим угловой коэффициент прямой AB
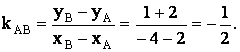
Таким образом, kCD = 2. Подставив координаты точки C(-1; 2) и угловой коэффициент kCD = 2 в формулу уравнения прямой с угловым
коэффициентом, получим уравнение прямой CD
у – 2 = (2х - 2) или 2х – у + 4 = 0.
w Так как прямые АВ и ЕС параллельны, то
по условию параллельности двух прямых kАВ =
kЕС. Тогда 
и уравнение прямой ЕС
принимает вид: у - 2 = -1/2(х + 1) или 2у – 4 = - (х + 1) и, окончательно, х +
2у – 3 = 0.
x Найдем координаты точки М. Так как СМ -
медиана, то точка М является серединой отрезка АВ и
Так как хМ
= хС, то уравнение СМ имеет вид: х = -1.
y Найдем угол a между прямыми ВМ1 и ВС,
используя формулу тангенса угла между двумя прямыми. Предварительно вычислим
угловые коэффициенты прямых ВМ1 и ВС. Точка М1 является
серединой отрезка АС и, следовательно, как и в предыдущем случае ее координаты
, 
,
т.е. М1(1/2;0).
Тогда,
,
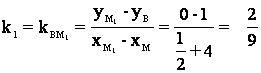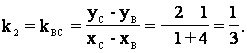
и
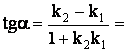
т.е. 
.
z Для определения координат точки
пересечения медиан треугольника, достаточно знать уравнения двух его медиан. Выше
было найдено, что уравнение медианы СМ. Найдем уравнение медианы ВМ1,
используя формулу уравнения прямой, проходящей через две заданные точки.
Получаем
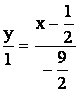или 
После преобразования получаем уравнение
медианы BM1
в общем виде
2x + 9y – 1 = 0.
Точка К лежит и на прямой
СМ и на прямой ВМ1. Следовательно, координаты удовлетворяют
уравнениям обеих прямых. Значит, для вычисления координат точки К достаточно
решить систему уравнений, содержащую уравнения первой и второй прямых.
~ 
~ 
~ 
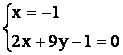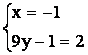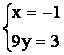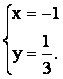
Итак, точка
пересечения медиан треугольника 
.
{ Площадь треугольника может быть
вычислена по формуле 
, где a =
½AB½ - длина основания, h = ½CD½- длина высоты треугольника. В нашем примере длина основания
треугольник ½AB½ = 3
(было
вычислено выше, см 1.). Длину высоты СД найдем как расстояние от точки C до прямой AB. Для этого определим сначала общее
уравнение прямой АВ. Имеем
или после преобразований х +2у + 2 = 0.
Таким образом, А = 1, В = 2, С = 2. Кроме того, из условия известны координаты
точки С: хС =-1, уС = 2. Тогда, по формуле расстояния от
точки до прямой, имеем
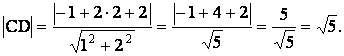
Следовательно, площадь треугольника
.
}
Сделаем
чертеж.
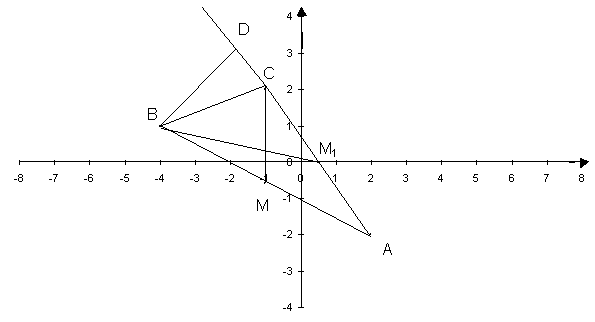
Для того, чтобы записать
систему неравенств, определяющих треугольник, необходимо знать уравнения всех
трех сторон. Найдем уравнения всех сторон треугольника. Уравнение прямой АВ - х
+2у + 2 = 0 - было найдено выше (см. 7). Найдем теперь уравнения прямых ВС и
АС, используя формулу прямой, проведенной через две заданные точки. Для прямой
ВС имеем
или после преобразований х – 3у + 7 = 0.
Для прямой АС аналогично получаем
или после преобразований 4х + 3у –2 = 0.
Теперь определяем систему неравенств. По чертежу видно, что точка с
координатами (0, 0) лежит внутри треугольника. Каждая прямая делит плоскость на
две полуплоскости. Подставим в каждое уравнений прямой координаты точки (0, 0)
и определим вид неравенства.
Для
прямой АВ, после подстановки координат (0, 0) получаем:
0 + 2×0 + 2 = 2.
Так как 2 ³ 0, то соответствующее неравенство имеет
вид
х + 2у + 2 ³ 0.
Подставим в уравнение прямой ВС
координаты точки (0, 0)
0 - 3×0 + 7 = 7.
Так как 7 ³ 0, то неравенство имеет вид
х - 3у + 7 ³ 0.
Подставим в уравнение прямой АС
координаты точки (0, 0)
4×0 + 3×0 - 2 = - 2.
Так как –2 £ 0, то получаем неравенство 4х +3у –2 £ 0.
Отсюда система линейных неравенств,
определяющих треугольник АВС
