Глава VI

Линейная алгебра

1. Системы линейных уравнений

1.1. Понятие о системах линейных уравнений

 

         Теория систем линейных уравнений закладывает основу большому и важному разделу алгебры - линейной алгебре.

В отличие от элементарной алгебры мы будем изучать системы с произвольным числом уравнений и неизвестных.

Пусть нам дана система из n уравнений с n неизвестными

 

                                                                                   (1.1)

 

Здесь х1, х2, ..., хn - неизвестные. Все они в первой степени (поэтому система называется линейной), а коэффициент i-го уравнения при j-том неизвестном обозначается через aij и bi - свободный член i-го уравнения.

         Коэффициенты при неизвестных составляют прямоугольную таблицу

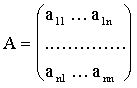                                                                       ,                                                  (1.2)

которая называется матрицей из n строк и n столбцов. Еще эту таблицу называют квадратной матрицей.

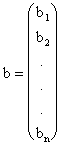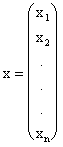                                                                       ,                                                (1.3)

b и x называются соответственно матрица-вектор b свободных членов и матрица-вектор х неизвестных.

Теперь (1.1) можно записать в виде

                                                                         Ах = b                                                                (1.4)

         Решением системы линейных уравнений (1.1) (а также (1.4), так как это эквивалентные записи) называется система n чисел k1, k2, ..., kn таких, что каждое из уравнений (1.1) обращается в тождество после замены хi на ki.

Если система линейных уравнений не имеет ни одного решения, то она несовместна. В противном случае она называется совместной.

         Система называется определенной, если она обладает одним единственным решением, и неопределенной, если решений больше, чем одно.

         Задача теории систем линейных уравнений состоит в разработке методов, позволяющих узнать, совместна данная система уравнений или нет, и если совместна, то установить число решений, а также указать способ нахождения всех решений.

         Начнем с метода, наиболее удобного при практическом применении.

 

1.2. Метод Гаусса для решения систем линейных уравнений со многими неизвестными

        

Этот метод иногда еще называют методом последовательного исключения неизвестных.

Чтобы упростить изложение метода, рассмотрим систему из четырех уравнений и четырех неизвестных. Считаем, что система совместна.

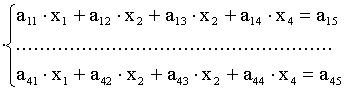                                                                               (2.1)

I. Пусть а11 ¹ 0 (ведущий коэффициент). Тогда разделим все члены первого уравнения на а11:

                    

                                               х1 + b12×x2 + b13×x3 + b14×x4 = b15,                                     (2.2)

где

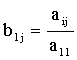, (j > 1)                  (*).

 

Полученное уравнение (2.2) умножим на а21, получим

а21×х1 + а21×b12×x2 + a21×b13×x3 + a21×b14×x4 = a21×b15.

 

Это уравнение вычтем из второго уравнения исходной системы (2.2):

 .

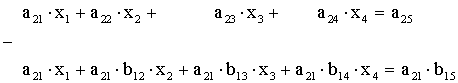В результате имеем

 

Повторим такую операцию со всеми оставшимися уравнениями. В результате получим систему

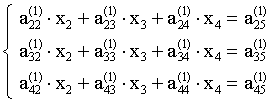                                                                                                (2.3)

Здесь

                                                 ,    (i,j ³ 2)                                   (2.4)

II. Считаем, что в системе (2.3) ведущий элемент .

Повторим этап I.

                                               ,                                     (2.5)

где

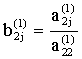,   (j > 2).

Повторим процедуру (*) из этапа I. В результате получим систему, но уже без х2

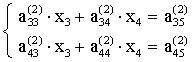                                               ,                                         (2.6)

где

                                               ,  (i,j ³ 3)                                   (2.7)

III.  Теперь считаем, что , и аналогичным образом приходим к уравнению

                                               ,                                                 (2.8)

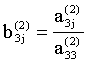,   (j > 3).

Получим систему из одного уравнения

                                                         ,                                                        (2.9)

 

 

IV.  Пусть теперь . Тогда

                                               ,  (i,j ³ 4).                             (2.10)

Теперь

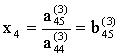 .                                                   (2.11)

И так далее, если работаем с системой более, чем из 4-х уравнений.

Эта часть (См.выше) вычислений называется прямым ходом метода Гаусса.

Таким способом мы получим приведенные уравнения

.

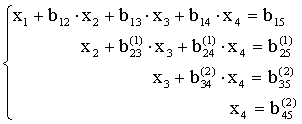Из них мы последовательно находим неизвестные (обратный ход)

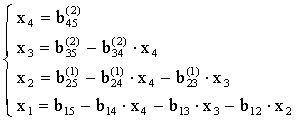                                               .                                    (2.12)

 

З а м е ч а н и е . Если  на каком-либо этапе окажется равным нулю, то уравнения системы надо переставить надлежащим образом.

При решении системы уравнений удобно результаты вычислений заносить в следующую таблицу:

 

 

х1

 

 

х2

 

х3

 

 

х4

свободный член

 

S

 

Этапы

а11

а21

а31

а41

a12

a22

a32

a42

a13

a23

a33

a43

a14

a24

a34

a44

a15

a25

a35

a45

a16

a26

a36

a46

 

 

А0

1

b12

b13

b14

b15

b16

 

 

 

 

a(1)22

a(1)32

a(1)42

a(1)23

a(1)33

a(1)43

a(1)24

a(1)34

a(1)44

a(1)25

a(1)35

a(1)45

a(1)26

a(1)36

a(1)46

 

А1

 

1

b(1)13

b(1)14

b(1)15

b(1)16

 

 

 

a(2)33

a(12)43

a(2)34

a(2)44

a(2)34

a(2)44

a(2)36

a(2)46

 

A2

 

 

1

b(2)14

b(2)15

b(2)16

 

 

 

 

 

a(3)44

a(3)46

А3

 

 

 

1

b(3)15

b(3)16

 

 

 

 

1

 

 

1

 

1

 

 

1

 

 

 

x4

x3

x2

x1

 

В

 

 

Для проверки вычислений полезно использовать “контрольные суммы”:

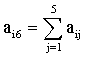     (i = 1, 2, ..., 5)

.

Пример.

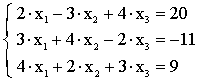
Применим описанный выше метод.

Применение его приведет нас к следующей таблице:

                 

x1

x2

x3

b

S

 

2

3

4

1

-3

4

2

1.5

4

-2

3

2

20

-11

9

10

23

-6

18

11.5

 

А0

 

8.5

8

1

-8

-5

-0.63

-41

-31

-3.87

-40.5

-28

-3.5

 

А1

 

 

-2.69

1

-8.07

3

-10.75

4

А2

 

 

1

 

1

1

3

-2

1

4

-1

2

 

В

 

 

Метод, изложенный выше, весьма прост и без труда реализуется на вычислительных машинах, однако он не дает возможности сформулировать условия совместимости или определенности системы при помощи коэффициентов и свободных членов этой системы. Поэтому теорию развивают другим методом.

 

2. Матрицы и определители

2.1. Вводные замечания

 

Определение 1. Множество, состоящее из m´n чисел, расположенных в таблице (прямоугольной), представляющей собой m строк и  n столбцов

,

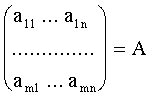называется матрицей (численной).

 

         Числа аij (i = 1¸m, j = 1¸n), составляющие матрицу, называются ее элементами.

Существуют другие формы записи матрицы:

(i=1¸m, j=1¸n)

или

.

         В рассматриваемом случае также говорят, что мы имеем матрицу порядка m´n.

                   Если m = n, то А называют квадратной матрицей порядка n.

                   Если m ¹ n, то А называют прямоугольной.

                   В частном случае 1´n матрицу называют вектор-строка, а в случае m´1 - вектор-столбец.

Матрица вида 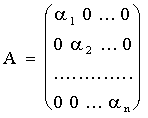                          называется диагональной.

Если ai = 1 (i = 1¸n), то вводят обозначение А = Е и тогда называют матрицу единичной. Таким образом, матрица Е всегда имеет вид

.

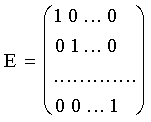Вводится также так называемый символ Кронеккера:

.

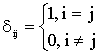Если для любого значения i,j aij º  0, то А называют нулевой матрицей и вводят обозначение А= [0]mn.

Если матрица А - квадратная, то есть , то она имеет определитель (детерминант):

.

 

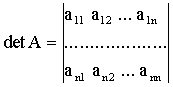З а м е ч а н и е. Не нужно смешивать эти два понятия. Матрица - это упорядоченное множество чисел, представленное в форме таблицы, а  detA - число, вычисленное по определенной формуле:

,                                      (1.1)

где сумма берется по всем возможным комбинациям (a1, a2, ..., an) элементов 1,2,...,n , а всего n! членов.

 

2.2. Операции над матрицами

 

         I. Матрицы  и  называются равными А = В, если m = p,

 a n = q и aij = bij.

 

         II. Пусть , .

Тогда А + В = С означает, что  матрица того же порядка, как А и В, и сij = aij + bij есть сумма соответствующих элементов, то есть

.

 

         Для суммы матриц справедливы следующие свойства:

 

                                      1. А + (В + С) = (А + В) + С.

                                      2. А + В = В + А.

                                      3. А + 0 = А.

Для разности матриц имеют место аналогичные свойства.

 

         III. Умножение матрицы на число

,

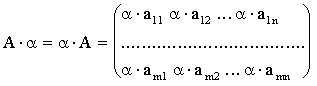где a - константа.

         Для этой операции справедливы следующие свойства:

                            1. 1×А = А.

                            2. А×0 = 0.

                            3. a×(b×А) = (a×b)×А.

                            4. (a + b)×А = a×А + b×А.

                            5. a×(А + В) = a×А + a×В.

Здесь А,В - матрицы, а a, b - числа.

         В ситуации -1×А вводится обозначение  -А  (то есть –А = -1×А) и говорят, что матрица  -А называется противоположной А.

         В частности А - В = А + (-В).

 

         IV. Произведение двух матриц

                                      Пусть  и   .

Если n = p (то есть число столбцов n  матрицы А равно числу строк  р матрицы В), то матрица  называется матрицей произведения А×В, то есть

,

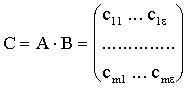где

                                     сij = ai1×b1j + ai2×b2j + ... + ain×bnj  .                                   (2.1)

 

З а м е ч а н и е.   В общем случае А×В ¹ В×А.

 

         Для этой операции справедливы следующие свойства:

                            1. А×(В×С) = (А×В)×С.

                            2. a×(А×В) = (a×А)×В, a - константа.

                            3. (А+В)×С = А×С+В×С.

                            4. С×(А+В) = С×А+С×В.

 

З а м е ч а н и е. Из существования А×В не следует существование В×А.

         В частном случае, когда  А×В = В×А,   говорят, что матрицы А и В коммутативны.

 

Пример.

         Если , то А×Е = Е×А=А.

 

Примеры.

                   1. Пусть        ,     .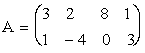

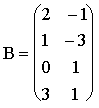Тогда

 

.

 

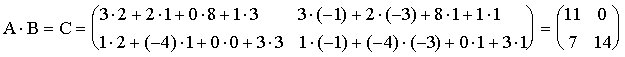                   2. Пусть

, .

;      .

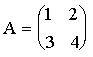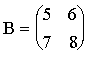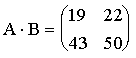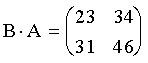                   3. Пусть

,        .

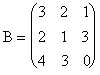,     но В×А - не существует.

 

         V. Транспонирование матриц

                   Пусть дана матрица

,    то матрица

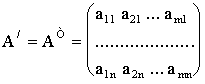
называется транспонированной по отношению к матрице А.

        

Эта операция обладает следующими свойствами:

                            1. Матрица, транспонированная дважды, совпадает с начальной.

А// = (А/)/ = А.

                            2. (A + B)/ = A/ + B/.

                            3. (A×B)/ = B/×A/.

                            4. Если А/ = А, то матрица А называется симметричной.

 

Если m = n, то аij = аji по отношению к  основной диагонали.

Например, С = А×А/  -  матрица симметричная.

                   С/ = (А×А/)/ = (А/)/×А/ = А×А/ = С.

 

         VI. Обратная матрица

 

Определение 2.1. Матрица В называется обратной матрицей по отношению к данной матрице А, если

А×В = В×А = Е,

где Е - единичная матрица. Тогда В будем обозначать А-1.

 

         Таким образом,     А×А-1 = А-1×А = Е                                                      (2.2)

 

 

         VII. Подобные матрицы

 

Определение 2.2. Квадратные матрицы А и В называются подобными, если они связаны равенством

В = Q-1×A×Q.

 

При этом говорят, что матрица В получена из матрицы А транспонированием матрицы Q.

 

 

2.3. Определитель

 

         Дадим вначале определение определителя второго и третьего порядка.

Под определителем второго порядка  мы будем понимать число, которое определяется по следующему правилу:

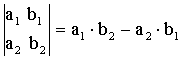                                               ,                                           (3.1)

где а1, а2, b1, b2 - действительные числа.

 

         Определитель второго порядка равен разности произведений элементов его первой и второй диагонали.

С помощью этого понятия удобно решать систему двух уравнений с двумя неизвестными. (Метод Крамера).

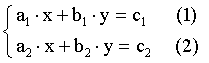
Для нахождения решений системы применим метод исключения неизвестных, умножив (1) на b2, a (2) на (-b1) и сложив результаты перемножений получим

(a1×b2 - a2×b1)×х = c1×b2 - c2×b1.

         Аналогично поступив по отношению к у, то есть умножая (1) на (-а2), а (2) на а1, получаем

(a1×b2 - a2×b1)×y = a1×c2 - a2×c1.

Введем в рассмотрение определители:

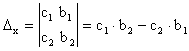
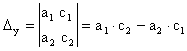
Тогда для того, чтобы найти решение системы, мы должны потребовать выполнения следующего неравенства D ¹ 0.

Заметим, что вспомогательные определители Dх и Dу получаются из D заменой  соответственно первого или второго столбца столбцом свободных членов.

Таким образом

                                               ,     .                                                (3.2)

 

Теорема 2.1.  Если D ¹ 0, то система уравнений имеет единственное решение, и оно определяется по правилу Крамера (3.2).

 

         Распространим понятия определителя и детерминанта на случай третьего порядка.

         Пусть дана система уравнений

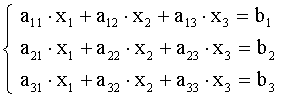                                               .                              (3.3)

,

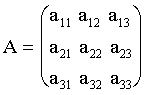                   .                    (3.4)

 

         Дадим без доказательства (пока) способ вычисления определителя третьего порядка:

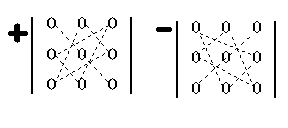
         Для доказательства (2.7) введем понятия минора и алгебраического дополнения.

 

 

Определение 2.3. Под минором элемента определителя понимается определитель младшего порядка (второго), получающийся из данного определителя в результате вычеркивания строки и столбца, содержащего данный элемент.

 

Определение 2.4. Алгебраическим дополнением (минором со знаком) элемента определителя называется минор этого элемента, взятый со знаком ‘+’, если сумма индексов элемента (i + j) - четное число, или со знаком ‘-’, если сумма индексов элемента (i+j) - нечетное число.

.

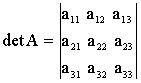Для элемента а23 имеем минор

 ,

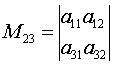а алгебраическое дополнение

.

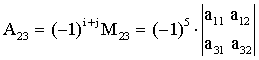Тогда

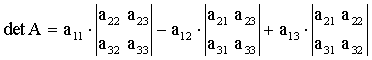                            .                            (3.5)

Если det A = D ¹ 0, то систему (3.3) можно решить методом Крамера

                           

,  ,  .

 

 

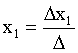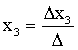2.4. Основные свойства определителей

 

         1. Определитель не меняет своего значения при замене всех его строк соответствующими столбцами.

.

        

2. При перестановке двух параллельных рядов определителя его абсолютная величина сохраняет прежнее значение, а знак меняется на противоположный.

Следствие 1. Определитель, у которого два параллельных ряда одинаковы, равен нулю.

Следствие 2. Сумма парных произведений элементов какого-нибудь ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

 

         3. , если А имеет порядок  n, то есть общий множитель элементов какого-либо ряда можно выносить за знак  определителя.

 

         4. , если А и В одного порядка.

 

         5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей:

.

 

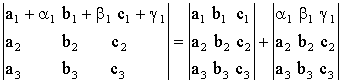a   Все свойства доказать самостоятельно в качестве упражнения.

 

Определение 2.5. Матрица называется регулярной, если ее определитель отличен от нуля.

 

Теорема 2.2. Все регулярные матрицы имеют обратную матрицу.

 

         Д о к а з а т е л ь с т в о :

         Пусть

 

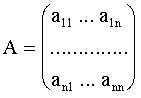
 и  (в этом случае матрица называется невырожденной).    Построим для матрицы А матрицу А*, составив ее из алгебраических дополнений к элементам матрицы А. Транспонируя ее, имеем

  

 

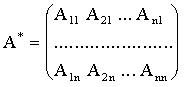
Это так называемая присоединенная или взаимная матрица.

Разделим все элементы матрицы А на D:

 

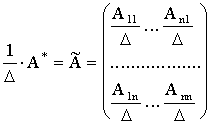
Докажем, что .

Действительно,

         и

,

         где

.

В силу свойств 1-5 имеем:

         1. Сумма произведений элементов какой-либо строки или столбца определителя на их алгебраические дополнения равна нулю или D.

         2. Сумма произведений элементов какой-либо строки или столбца определителя на алгебраические дополнения соответствующих элементов других строк или столбцов равна нулю.

Тогда

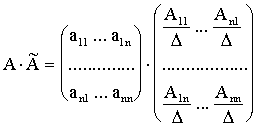
Тогда по определению

.

Аналогично доказывается

.

Окончательно

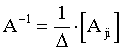                                                        .                                              (4.1)

 

З а м е ч а н и я.

         1. Если для матрицы А существует А-1, то она единственная.

Пусть матрица В такова, что А×В=Е. Тогда А-1×А×В=А-1×Е и, следовательно, В=А-1.

         2. Если матрица А сингулярная, то есть , следовательно, она не имеет обратной матрицы.

Известно, что

.

По свойствам операции умножения и условию имеем, что

 и, следовательно, 0=1, что нелепо, то есть наше утверждение верно.

2.4.1. Свойства обратной матрицы

 

         1. Определитель обратной матрицы обратно пропорционален определителю начальной матрицы

                                                        .                                       (4.1.1)

Д о к а з а т е л ь с т в о :

         А-1×А = E, следовательно, , а отсюда следует (4.1.1).

         2. Обратная матрица произведения двух матриц равна произведению обратных матриц сомножителей, взятых в обратном порядке

                                                        (А×В)-1 = В-1×А-1.                                                           (4.1.2)

Д о к а з а т е л ь с т в о :

А×В×(В-1×А-1) = А×(В×В-1)×А-1 = А×Е×А-1 = А×А = Е

         и

В-1×А-1×(А×В) = В-1×(А-1×А)×В = В-1×Е×В = В-1×В = Е.

 

Следовательно, по определению (2.1)    В-1×А-1 - обратная матрица для А×В.

 

         3. Транспонированная обратная матрица равна обратной транспонированной матрице

                                               (А-1)/ = (А/)-1.                                                   (4.1.3)

 

Д о к а з а т е л ь с т в о :

         По определению (2.1) А-1×А = Е, тогда

(А-1×А)/ = А/×(А-1)/ =Е/ = Е.

Умножим это равенство на (А/)-1:

(А/)-1×А/×(А-1)/ = (А/)-1×Е,

         следовательно,

(А-1)/ = (А/)-1.

З а м е ч а н и е.

         Понятие обратной матрицы дает простое решение системы уравнений, записанное в матричной форме

А×Х = В   и   Y×А = B

А ¹ 0, следовательно, Х = А-1×В   и   Y = B×A-1, где, например,

,   ,  

 

.

 

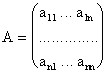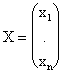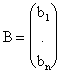
3. Ранг матрицы

         Пусть дана матрица

.

Если в матрице А выбрать произвольным образом k строк и k столбцов (где k=min(m,n)), то получим подматрицу А матрицы. (Элементы, стоящие на пересечении отмеченных строк и столбцов).

 

         Определитель каждой из таких матриц

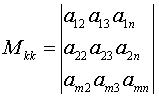
называется минором порядка k матрицы А.

 

Определение 3.1. Наивысший порядок отличных от нуля миноров матрицы А называется ее рангом.

 

         Иначе говоря, матрица имеет ранг k , если .

                   -  по крайней мере один из миноров порядка k отличен от нуля.

                   -  все миноры порядка k + 1 равны нулю.

Пример.

Определить ранг матрицы

.

 

.

 

.

,            ,  ... .

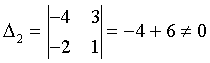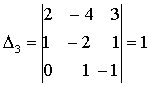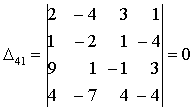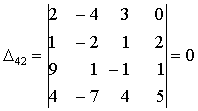         Таким образом, r = 3.

 

Теорема 3.1. (Кронеккера-Копелли). Система линейных уравнений совместима тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы.

(без доказательства).

 

Назад  Далее