Глава V
Ряды и
понятие о сходимости рядов
1. Числовые ряды
1.1. Определение ряда и его сходимость
В настоящей главе обобщим понятие суммы
на некоторые случаи бесконечного числа слагаемых и изучим свойства таких сумм.
Определение 1. Пусть задана
последовательность чисел
а1,
а2, а3, ..., аn, ...
(1.1)
Выражение
вида
![]() (1.2)
(1.2)
называется
рядом, а число аn - его n-ным членом, n = 1,2,... .
Сразу же заметим, что в нашем случае
(1.2) - числовой ряд. Если же последовательность ![]() есть
последовательность функций, то ряд называется функциональным (аn = fn(x), n = 1,2,...).
есть
последовательность функций, то ряд называется функциональным (аn = fn(x), n = 1,2,...).
Примеры.
аn = а×qn-1, ![]() .
.
Понятно, что изучение функциональных
рядов всегда можно свести к изучению числовых рядов, зафиксировав х = х0.
Ряд (1.2) считается заданным, если мы
знаем его общий член аn (то есть член, стоящий на n-ном месте). Из
теории последовательностей мы знаем, что аn выражается как функция
номера n.
Определение 2. Конечная сумма первых n
членов ряда называется n-й частичной
суммой, а оставшиеся члены, начиная с n + 1, написанные в том же порядке,
что и в данном ряду, называется n-ным
остатком ряда.
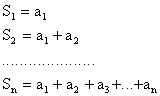 (1.3)
(1.3)
Sn
- n-ная частичная сумма (n = 1,2,...,k)
Rn = an+1 + an+2 + ... + an+i +
... , (1.4)
Rn - остаток ряда.
Определение 3. Ряд ![]() называется сходящимся, если последовательность его
частичных сумм
называется сходящимся, если последовательность его
частичных сумм ![]() сходится. Если ряд не сходится, то говорят, что он расходится.
сходится. Если ряд не сходится, то говорят, что он расходится.
Если ряд сходится, то ![]() называется его суммой.
называется его суммой.
![]() . (1.5)
. (1.5)
Если
![]() , то
, то 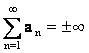 .
.
Если ряд ![]() - функциональный, то
есть un = fn(x), то для каждого фиксированного аргумента
х числовой ряд f1(x0) + f2(x0) + f3(x0)
+ ... или сходится, или расходится. Соответственно этому точку х будем называть
точкой сходимости или точкой расходимости.
- функциональный, то
есть un = fn(x), то для каждого фиксированного аргумента
х числовой ряд f1(x0) + f2(x0) + f3(x0)
+ ... или сходится, или расходится. Соответственно этому точку х будем называть
точкой сходимости или точкой расходимости.
Совокупность всех точек сходимости
функционального ряда называется областью
сходимости данного ряда.
Если un = fn(x)
(n = 1,2,...) и функциональный ряд ![]() сходится в каждой
точке некоторого множества, то говорят, что он сходится на этом множестве, а
функция S = S(x), определенная для каждого фиксированного значения из этого
множества, называется суммой этого ряда
на данном множестве
сходится в каждой
точке некоторого множества, то говорят, что он сходится на этом множестве, а
функция S = S(x), определенная для каждого фиксированного значения из этого
множества, называется суммой этого ряда
на данном множестве
![]() .
.
Пусть
Rn = S - Sn, тогда Rn - остаток ряда и
представляет собой погрешность,
которая получается, если в качестве суммы ряда взять Sn .
![]() .
.
Тогда
понятно, почему первой и основной задачей теории рядов будет исследование
сходимости ряда.
Пример. Исследовать на сходимость
ряд:
1. а + а×q + а×q2 + ... (a ¹ 0)
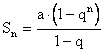 .
.
Рассмотрите
четыре случая:
1)
![]() ; 2)
; 2) ![]() ;
;
3)
q = -1; 4) q = 1.
2. Доказать сходимость ряда
![]()
![]()
Отсюда
![]() следовательно,
следовательно, ![]() .
.
Таким
образом имеем
![]() .
.
1.2. Сходимость ряда (свойства)
Теорема 2.1. Сходимость ряда не
нарушается, если все его члены умножать на одно и то же число, отличное от нуля
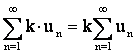 , где k не является константой.
, где k не является константой.
Д о
к а з а т е л ь с т в о:
![]()
Так как ![]() , то имеем, что
, то имеем, что![]() .
.
Под
суммой (разностью) двух рядов
![]() ,
, ![]()
будем понимать соответственно ряд вида
![]() .
.
Теорема 2.2. Сумма (разность) двух
сходящихся рядов есть ряд сходящийся, причем
![]() . (2.1)
. (2.1)
Д о
к а з а т е л ь с т в о :
Для любого конечного числа N
![]() , но
, но
![]() и
и ![]() согласно условию
теоремы. Тогда
согласно условию
теоремы. Тогда
![]() .
.
Теорема
2.3. (Необходимый признак сходимости ряда).
Если ряд ![]() сходится, то
сходится, то
![]() .
.
Д о
к а з а т е л ь с т в о :
Пусть
Sn-1
= a1 + a2 + ... + an-1;
Sn = a1 +
a2 + ... + an-1 + an.
Тогда
an = Sn - Sn-1, и так как данный ряд сходится,
то имеем, что ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() .
.
Следствие. Если ![]() , то ряд расходится.
, то ряд расходится.
З а м е ч а н и е. Сходимость к нулю члена
ряда аn не является достаточным признаком сходимости ряда.
Пример.
![]() - гармонический ряд.
- гармонический ряд.
![]() .
.
Покажем,
что ряд расходится.

Очевидно,
что
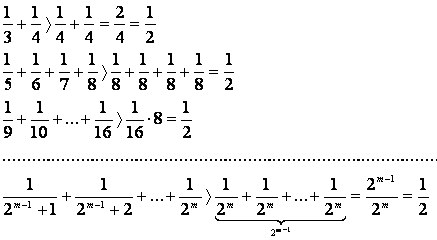 .
.
Таким
образом ![]() ; полагая n = 2m, имеем, что если n®¥, то и m®¥, следовательно,
; полагая n = 2m, имеем, что если n®¥, то и m®¥, следовательно,
 .
.
Следовательно,
ряд расходится.
1.3. Признак
сравнения рядов
Пусть теперь необходимое условие
выполнено, то для определения сходимости ряда нужно воспользоваться какими-то
достаточными признаками сходимости.
В
дальнейшем мы будем использовать нижеследующую лемму.
Лемма 3.1. Если в ряде
а1 + а2
+ ... + ар + ар+1 + ... (3.1)
отбросить
конечное число его первых членов, то остаток ряда
Rр = aр+1
+ aр+2 + ...
(3.2)
будет
сходиться или расходиться одновременно с данным рядом.
Д о
к а з а т е л ь с т в о :
Пусть
Q =
a1 + a2 + ... + ap,
a
Sn - конечная сумма ряда
(3.1)
![]() - конечная сумма ряда (3.2)
- конечная сумма ряда (3.2)
Тогда
![]() , следовательно,
, следовательно, ![]() .
.
Предположим,
что (3.1) сходится и ![]() . Тогда и
. Тогда и ![]() . В этом случае
. В этом случае ![]() , что свидетельствует о сходимости ряда (3.2).
, что свидетельствует о сходимости ряда (3.2).
Предположим
теперь, что ряд (3.2) сходится. Тогда ![]() и, следовательно,
и, следовательно, ![]() , поэтому ряд (3.1) тоже сходится.
, поэтому ряд (3.1) тоже сходится.
Следствие. При исследовании
сходимости ряда можно игнорировать конечное число его членов.
Теорема 3.1. (признак сравнения). Если члены ряда неотрицательны и не превышают
соответствующих членов сходящегося ряда, то данный ряд сходится.
Д о
к а з а т е л ь с т в о :
Пусть дан ряд
а1 + а2 + ... + аn +
... ,
который
необходимо исследовать на сходимость.
А
ряд ![]() - сходится, и
выполняется следующее условие
- сходится, и
выполняется следующее условие
ai £ bi (I = 1,2,...).
Пусть
Sn=a1+a2+...+an,
![]() .
.
Так
как ряд ![]() сходится, то
следовательно,
сходится, то
следовательно, ![]() , где S/ - сумма ряда.
, где S/ - сумма ряда.
Согласно
условию теоремы
0 £ a1 £ b1, 0 £ a2 £ b2, ..., 0
£ an £ bn, ...
Но
тогда ![]() . Следовательно, Sn представляют собой
ограниченную монотонно возрастающую последовательность, то есть имеет предел.
. Следовательно, Sn представляют собой
ограниченную монотонно возрастающую последовательность, то есть имеет предел.
А
это и доказывает сходимость ![]() .
.
Следствие. Если дан ряд, и его члены
не меньше соответствующих членов знакоположительного ряда и этот второй ряд
расходится, то и данный ряд будет расходиться.
Действительно,
если бы данный ряд сходился, то, по доказанной теореме, и второй ряд бы
сходился, что противоречит нашему условию.
Пример. Задан ряд (1) исследовать
его на сходимость.
1. ![]() сравним его с рядом
(2)
сравним его с рядом
(2)
2. ![]() сравним их n члены
сравним их n члены
![]() (n=2,3, ...)
(n=2,3, ...)
2 -
гармонический расходящийся ряд, следовательно, 1 - расходится.
1.4. Признак сходимости Даламбера
Рассмотрим некоторые специальные
признаки сходимости ряда. Отметим среди них признак Даламбера и признак Коши.
Теорема 4.1. (признак Даламбера). Пусть дан ряд с положительными членами
![]() , un >
0, n=1,2, ...
(4.1)
, un >
0, n=1,2, ...
(4.1)
Тогда
1. Если существует q такое, что 0 < q < 1 и существует n0
такое, что ![]()
![]() для любого n > n0,
то ряд (4.1) сходится;
для любого n > n0,
то ряд (4.1) сходится;
2. Если существует n0 такое,
что для любого n > n0 ![]() , то ряд (4.1) расходится.
, то ряд (4.1) расходится.
То есть если ![]() .
.
Следствие.
1. при q < 1 ряд сходится;
2. при q > 1 ряд расходится;
3. при q = 1 необходимо дополнительное
исследование; ряд может и сходиться, и расходиться.
Д о
к а з а т е л ь с т в о :
Пусть ряд (4.1) состоит из
положительных членов и пусть
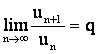 .
.
1.
При 0 < q < 1 существует n0 такое, что при n > n0
![]() , то есть un+1 £ q×un при любом n > n0, то есть
, то есть un+1 £ q×un при любом n > n0, то есть
![]() ,
,
![]() ,
,
..............................................
![]() ,
,
.....................................................
а
так как ряд
![]()
сходится,
являясь геометрической прогрессией со знаменателем q (0 < q < 1), то по
признаку сравнения сходится и ряд
![]() ,
,
но
это остаток ряда ![]() , который сходится. Тогда согласно лемме и весь ряд (4.1)
сходится.
, который сходится. Тогда согласно лемме и весь ряд (4.1)
сходится.
2. Пусть q>1. Выберем e такое, что q-e>1 для любого n³n0 ![]() имеем
имеем
![]() ,
, ![]() , ...
, ...
Так
как по предположению член ряда un > 0 и ограничен снизу
положительной константой, то ![]() , и, следовательно, ряд расходится.
, и, следовательно, ряд расходится.
3. q = 1. На примерах можно показать,
что ряд в одних случаях сходится, а в других расходится.
Замечание.
1. Если ряд (4.1) функциональный и un
= fn(x)>0 и l = l(x) - соответствующий предел, то 1,2,3
верны для каждого х.
2. Из теоремы следует (см. следствие
2), что если ![]() , то
, то ![]() .
.
Пример.
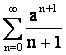 ,
, 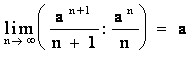 .
.
Каково поведение ряда при различных
значениях параметра а (a <
Если 0 < а < 1, то ряд расходится и
расходится при а > 1.
Если
а = 1, то признак Даламбера ответа не дает, но тогда имеем гармонический ряд
![]() ,
,
который
расходится.
Теорема 4.2. (признак Коши). Пусть дан ряд ![]() , аn ³ 0, (n = 1,2,...). Тогда:
, аn ³ 0, (n = 1,2,...). Тогда:
1.
Если существуют q и n0 такие, что 0 < q < 1 и для любого n ³ n0 выполняется
![]() , то ряд сходится.
, то ряд сходится.
2. Если существуют q и n0 такие, что 0 < q
< 1 и для любого n ³ n0 выполняется ![]() ,
,
то ряд
расходится.
Д о
к а з а т е л ь с т в о :
При n ³ 1 ![]() , то есть an£qn . Применим
признак сравнения.
, то есть an£qn . Применим
признак сравнения.
Если
![]() при 0 < q < 1
сходится, следовательно, ряд
при 0 < q < 1
сходится, следовательно, ряд ![]() тоже сходится.
тоже сходится.
Если
же ![]() , тогда и ряд расходится.
, тогда и ряд расходится.
Пример.
Исследуем на сходимость ряд ![]() .
.
![]() .
.
Таким
образом, исследуемый ряд сходится.
Следствие.
Пусть существует ![]() .
.
1. Если l < 1, то ряд сходится.
2. Если l > 1, то ряд расходится.
1.5.
Знакопеременные ряды и абсолютная сходимость
Рассмотрим ряды с вещественными
членами, знаки которых, вообще говоря, изменяются при изменении номера. Такие
ряды называются знакопеременными
рядами.
Теорема 5.1. Если для знакопеременного ряда ![]() сходится ряд,
составленный из абсолютных величин его членов
сходится ряд,
составленный из абсолютных величин его членов ![]() , то и данный ряд сходится.
, то и данный ряд сходится.
Д
о к а з а т е л ь с т в о :
Рассмотрим ряд ![]() . Так как
. Так как ![]() при всех n = 1,2, ...
при всех n = 1,2, ...
то ряд ![]() сходится. Hа основании
признака сравнения сходится и ряд
сходится. Hа основании
признака сравнения сходится и ряд ![]() ,
,
так как ![]() .
.
Замечание. Обратное утверждение
неверно. Если данный ряд сходится, то ряд из абсолютных величин его членов
может или расходиться, или сходиться.
Таким образом, все ряды
можно разбить на два класса:
1. К первому классу сходящихся рядов
отнесем ряды, которые сходятся сами, и при этом ряды, составленные из
абсолютных величин их членов, тоже сходятся - это так называемые абсолютно сходящиеся ряды.
2. Ко второму классу отнесем ряды,
которые сходятся сами, но при этом ряды, составленные из абсолютных величин их
членов, расходятся - это так называемые условно
сходящиеся или неабсолютно сходящиеся
ряды.
Пример.
![]() - абсолютно сходящийся
ряд ?
- абсолютно сходящийся
ряд ?
Данный ряд и ряд составленный из абсолютных величин дают нам ряды, которые
образуют геометрические прогрессии со знаменателями -1/2 и 1/2 и,
следовательно, сходятся.
1.6. Признак
сходимости Лейбница для знакопеременных рядов
Ряд вида
a1 -
a2 + a3 - a4 + ... + (-1)n-1×an +..., (6.1)
an
³ 0 при n = 1,2,3,...
называется знакопеременным (то есть
рядом стоящие члены имеют противоположные знаки).
Для таких рядов справедлива следующая
теорема.
Теорема 6.1. (Лейбница). Если абсолютные величины членов знакопеременного ряда
(6.1) монотонно убывают при n ® ¥, то есть
![]()
и ![]() , то ряд 6.1 сходится (вообще говоря, неабсолютно).
, то ряд 6.1 сходится (вообще говоря, неабсолютно).
Д о
к а з а т е л ь с т в о :
Рассмотрим конечную сумму ряда,
состоящего из 2m членов
S2m
= (a1 - a2) + (a3 - a4) + ...
+ (a2m-1 - a2m).
На
основании условия теоремы слагаемые в скобках положительны или равны нулю,
значит, S2m³0.
Если
число членов 2m возрастает, то S2m
- не убывает, так как каждый раз добавляются неотрицательные члены. Теперь
представим, что
S2m = a1 -
(a2 - a3) - (a4 - а5) - ... - a2m.
Но
тогда S2m £ a1, и тогда ![]() - монотонно
неубывающая последовательность и, будучи ограниченной последовательностью, она
стремится к некоторому пределу
- монотонно
неубывающая последовательность и, будучи ограниченной последовательностью, она
стремится к некоторому пределу
![]() .
.
Также
очевидно, что
S2m+1 = S2m +
a2m+1,
но
по условию теоремы ![]()
и
тогда имеем, что
![]() .
.
Получили,
что последовательность частных сумм ![]() при n ® ¥ стремится к одному и тому
же пределу S, но тогда ряд по определению сходится.
при n ® ¥ стремится к одному и тому
же пределу S, но тогда ряд по определению сходится.
З а м е ч а н и е. Погрешность при
приближенном вычислении суммы сходящегося знакопеременного ряда в условиях
теоремы по абсолютной величине не превышает абсолютной величины первого
отброшенного члена.
Пример.
![]() - сходится, так как
выполняются условия теоремы (6.1).
- сходится, так как
выполняются условия теоремы (6.1).
2. Понятие о функциональных рядах
2.1. Степенные
ряды
Ряд вида
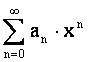 ,
(1.1)
,
(1.1)
составленный
по возрастанию целых степеней переменной х с коэффициентами
а0,
а1, а2 ..., не зависящими от х, называется степенным рядом.
Степенной ряд вида
а0 + а1×(х - а) + а2×(х - а)2 + ... +
аn×(х - а)n + ...,
где
а - константа, легко сводится к (1.1), если положить х – а = х/.
Поэтому проведем все рассуждения относительно
(1.1). Если зафиксируем х в (1.1), то будем получать числовые ряды, которые в
зависимости от значения х будут сходиться или расходиться.
Теорема 1.1.
Для любого степенного ряда вида (1.1) существует число R ³ 0 (радиус сходимости) такое, что если R > 0, то при ![]() ряд сходится, а при
ряд сходится, а при ![]() - ряд расходится. При
- ряд расходится. При ![]() ряд может как
сходиться, так и расходиться.
ряд может как
сходиться, так и расходиться.
(Без доказательства).
Интервал
(-R, R) называется интервалом сходимости.
Если
R = +¥, следовательно, интервал
сходимости - числовая прямая.
В
простейших случаях интервал сходимости может быть определен с помощью признака
Даламбера.
Рассмотрим ряд, составленный из
абсолютных величин
![]() .
.
Если
этот ряд сходится, то будет сходиться и ряд (1.1), причем абсолютно сходиться.
Воспользуемся
признаком Даламбера. Пусть
![]() , а
, а ![]()
Рассмотрим
отношение
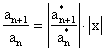 .
.
Предположим,
что существует
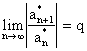 .
.
Тогда
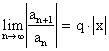 .
(1.2)
.
(1.2)
Из
(1.2) получаем условие сходимости.
1. Если ![]() , следовательно,
, следовательно, ![]() .
.
Отсюда
ряд S* сходится, следовательно, и ряд (1.1) сходится абсолютно.
2. ![]() , следовательно,
, следовательно, ![]() , следовательно, оба ряда расходятся.
, следовательно, оба ряда расходятся.
Но
тогда
![]()
есть
радиус сходимости, то есть
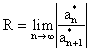 .
(1.3)
.
(1.3)
Вопрос
о сходимости на концах интервала х = -R
и x = R нужно решать особо.
Пример. Исследовать ряд
![]() .
.
Определим
радиус сходимости в силу (7.3) имеем
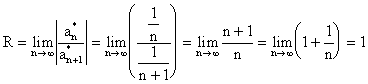 .
.
Таким образом ряд сходится для каждого
х, принадлежащего интервалу (-1,1).
При
х = -1 - ряд сходится условно.
При
х = 1 имеем ряд гармонический, он
расходится.
Таким
образом, областью сходимости данного ряда является [-1,1).
2.2. Разложение данной функции в ряд
Умение представить данную функцию в
виде степенного ряда дает возможность на практике вычислять значение этой
функции с любой степенью точности. Рассмотрим это на примерах.
1.
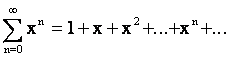
это
геометрическая прогрессия. При ![]() ряд сходится. Сумма
ряда
ряд сходится. Сумма
ряда ![]() .
.
Следовательно,
мы можем записать
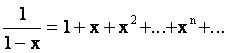 . (2.1)
. (2.1)
То есть 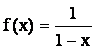 разложена в ряд по
степеням х.
разложена в ряд по
степеням х.
2. f(x) = ln(1 + x).
Для разложения заменим х на -z. Тогда
будем иметь в (8.1)
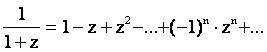 .
(2.2)
.
(2.2)
Если
![]() , то можно показать, что в интервале сходимости f(z)
дифференцируема или интегрируемая почленно. Умножая (2.2) на dz и интегрируя в пределах от 0 до х, получим
, то можно показать, что в интервале сходимости f(z)
дифференцируема или интегрируемая почленно. Умножая (2.2) на dz и интегрируя в пределах от 0 до х, получим
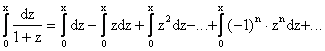 ,
,
то
есть
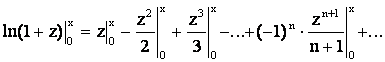 .
.
Окончательно
 , (x < 1).
, (x < 1).
Самостоятельно:
справедливо ли это разложение при х=1 ?
Пример:
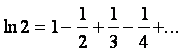 .
.
Пусть x = -z2 в разложении
(2.1).
Тогда
![]() ,
, ![]() .
.
Получим
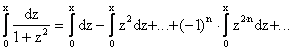
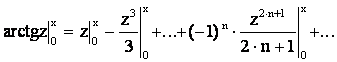 .
.
Так
как arctg0 = 0, окончательно имеем
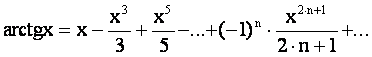 .
.
Доказать,
что разложение верно при х = 1 и х = -1.
Пример.
Вычислить
![]() .
.
2.3. Ряд
Маклорена
Решим теперь общий вопрос о разложении
данной функции f(x) в ряд по возрастающим целым степеням х.
.
Пусть,
например, f(x) представима в виде ряда
![]() . (3.1)
. (3.1)
Следовательно, необходимо определить
коэффициенты а0,а1,а2,...; причем интервал
сходимости ![]() не сводится к точке,
то есть R>0.
не сводится к точке,
то есть R>0.
Учтем
то, что степенной ряд (3.1) в интервале сходимости можно почленно
дифференцировать любое число раз и все полученные таким образом ряды тоже будут
сходиться, а их суммы равны соответствующим производным.
Продифференцируем
последовательно ряд (3.1):
f/(x) = a1 + 2×a2×x + 3×a3×x2 + ...
f//(x) = 2×a2 + 2×3×a3×x + 3×4×a4×x2 + ...
f///(x)
= 2×3×a3
+ 2×3×4×a4×x + 3×4×5×a5×x2 + ...
fIV(x) = 2×3×4×a4 + 2×3×4×5×a5×x + ...
........................................................................
Положим
теперь в этих равенствах и в (3.1) х =
0; тогда получим, что
f(0)
= a0; f/(0) = a1; f//(0) = 2×a2; f///(0) = 2×3×a3; fIV(0) = 2×3×4×a4;
...
То
есть а0 = f(0); ![]() ;
; ![]() ;
; ![]() ;
; ![]() ; ...
; ...
Подставляя
эти значения в (3.1), получим ряд
Маклорена:
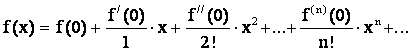 . (3.2)
. (3.2)
Пример.
1. f(x) = ex.
Так
как f(к)(x) = ex для
любого к. Пологая х = 0 , получим f(к)(0) = e0 = 1.
Тогда
ряд Маклорена имеет вид
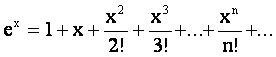 .
.
Исследуем ряд на сходимость.
![]() , следовательно, применяя признак Даламбера,
, следовательно, применяя признак Даламбера,
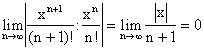 .
.
 , следовательно, ряд сходится для каждого х, принадлежащего
, следовательно, ряд сходится для каждого х, принадлежащего ![]() .
.
2. f(x) = Sinx.
f/(x)
= Cosx; f//(x) = -Sinx; f///(x) = -Cosx...
При х=0
имеем
f(0) = 0; f/(0) = 1; f//(0) = 0; f///(0) = -1.
Отсюда
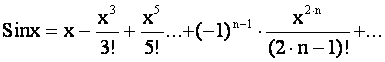 .
.
5. Вычислить Sin1, ![]() .
.
6. 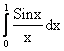 . (
. (![]() , f(0)=1).
, f(0)=1).
2.4. Ряд
Тейлора
Мы знаем, что в некоторых случаях f(x)
или ее производная неопределенны при х =
0: так, например, ведут себя функции f(x) = ln(x), ![]() , для которых
, для которых ![]() или
или ![]() . Следовательно, такие функции не могут быть разложены в ряд
Маклорена. Тогда нужно воспользоваться более общими степенными рядами.
. Следовательно, такие функции не могут быть разложены в ряд
Маклорена. Тогда нужно воспользоваться более общими степенными рядами.
Рассмотрим разложение в степенной ряд
функции f(x) по степеням (х-а), где а¹0 и его можно подобрать
соответствующим образом так, чтобы
f(x) = А0 + А1×(х - а) + А2×(х - а)2 + ... . (4.1)
Для
![]() (10.1) справедливо.
(10.1) справедливо.
Пусть
х - а = z.
Тогда
разложение (4.1) примет вид
F(z) = f(z + a) = А0 + А1×z + А2×z2 + ... , (4.2)
где ![]() . Но это уже ряд Маклорена.
. Но это уже ряд Маклорена.
Так
как F(n)(z) = f(n)(z + a), (n=1,2,...).
Таким
образом, имеем
A0 = F(0) = f(a),
![]() , ...,
, ..., ![]() , ...
, ...
Подставив
эти выражения в (10.2), получим ряд
Тейлора
![]() . (4.3)
. (4.3)
Если
а = 0, получим ряд Маклорена.
Если
в (4.3) взять конечное число членов, то вместо ряда Тейлора получим многочлен Тейлора
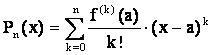 . (4.4)
. (4.4)
То
есть если (4.3) сходится в некоторой окрестности точки а (Ua), то
его сумма равна f(x), a Pn(x) дает приближенное представление f(x) в
Ua.
Пример.
Разложить многочлен
f(x) = x4 + 2×x2 - 6
по
возрастающим степеням (х - 2).
f/(x) = 4×x3 + 4×x; f//(x) = 12×x2 + 4; f///(x) = 24×x; f(IV)(x) = 24;
f(V)(x) = 0; f(n)(x) = 0 (n >
4).
При
х = 2 получим коэффициенты
разложения:
f(2) = 16 + 8 - 6 = 18; f/(2) = 40; f//(2) = 12; f///(2) = 48; f(IV)(2) = 24.
Таким
образом имеем следующее разложение
![]() ,
,
или
окончательно
f(x) = 18 + 40×(x-2) + 6×(x-2)2 + 8×(x-2)3 + (x-2)4.