Модуль №4.
Проверка статистических гипотез
Темы:
|
26. |
Проверка
статистических гипотез: |
|
27. |
Вопросы
для самопроверки:
·
Дайте определение статистической
гипотезы.
· Приведите примеры простой и сложной гипотез.
·
Приведите
примеры нулевой и конструирующей гипотезы.
·
Что
называют ошибкой
первого (второго) рода?
·
Как
находят критическую область?
·
Как
сравнивают средние, дисперсии?
·
Что
называют критерием
согласия?
·
Как
и для чего применяют критерий Пирсона?
Посмотри пример
выполнения заданий
Теперь переходим к контролю
Индивидуальные
задания к модулю № 4
Лучше поручить выбор Ваших заданий компьютеру.
Внимание
! Правильно выбери свои задания, например,
если Ваш вариант 3, то в модуле 4 Вы выполняете в Лаб.
3 в задаче 3.1- данные Л1, в задаче 3.2 – 3.5 8е - варианты .
Задания к лабораторной
работе 3
В задачах этой работы используются выборки из генеральных совокупностей с нормальным распределением ХÎN(m,s) (за исключением задачи 3.4).
По данной выборке при уровне значимости a проверить гипотезы в задачах:
3.1. Полагая, что s известно, нужно проверить гипотезу Но: m = mо , а в качестве альтернативной гипотезы можно использовать одну из следующих гипотез Н1: m < mо, Н1: m > mо или Н1: m ¹ mо.
Критическая
область определяется с помощью таблицы
«Функции распределения нормированного нормального
распределения
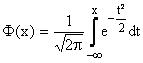
При известном s используем статистику 
.
Решить задачу, используя выборку и полученные результаты лабораторной работы 1, mо взять
равным ближайшему целому числу к 
, а a
=0,01.
3.2.
Проверить гипотезу: Но: m = mо при Н1: m ¹mо.
При неизвестном s
используем статистику t = 
.
Критическая область определяется с помощью таблицы «Функции t-распределения Стьюдента с числом степеней свободы n-1», где n-объем выборки.
3.3.
Проверить гипотезу о дисперсии нормального распределения ХÎN(m,s). Но:
s2
= 
при Н1: s2
< 
или Н1: s2
> 
(выбрать подходящую альтернативную
гипотезу).
Критическая область определяется с помощью таблицы «Функции c2-распределение Пирсона с числом степеней свободы n-1», где n-объем выборки.
3.4. Проверить гипотезу о распределении генеральной совокупности Х. Необходимо по выборке, или учитывая другие соображения, составить гипотезу Но о распределении генеральной совокупности. Для проверки гипотезы использовать c2- критерий согласия Пирсона.
3.5. Проверить гипотезу о равенстве центров распределения двух нормальных генеральных совокупностей:
а) при
известном s
используем статистику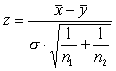 
.
Критическая область определяется с помощью таблицы функции Ф(х) (прил.2).
б) при неизвестных s1 и s2 , полагая s1 = s2 используем статистику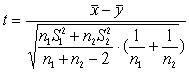 
.
Критическая область определяется с помощью таблицы «Функции t-распределения Стьюдента с числом степеней свободы n1 + n2 - 2», где n1, n2 -объемы выборок (прил.4).