Глава II
Дифференциальное
исчисление
1. Сходимость в пространстве Rn
1.1. Окрестности и пределы
последовательностей точек
Пусть
на рассматриваемой нами плоскости или пространстве всегда фиксирована некоторая
прямоугольная система декартовых координат. Точки будем обозначать большими
латинскими буквами ![]() , а их координаты - маленькими греческими, иногда с
индексами, т.е. в случае плоскости
, а их координаты - маленькими греческими, иногда с
индексами, т.е. в случае плоскости ![]() , а в случае
пространства
, а в случае
пространства ![]() . Расстояние между точками А и В будем обозначать
символом
. Расстояние между точками А и В будем обозначать
символом ![]() .
.
Как известно, формула для расстояния между точками A,B в случае плоскости имеет вид:
![]() ,
,
а в случае пространства:
![]() .
.
Определение1.1. Точкой Р
![]() -мерного пространства называется упорядоченная совокупность
-мерного пространства называется упорядоченная совокупность
![]() вещественных
чисел Р =
вещественных
чисел Р = ![]() или, короче, Р(xi).
Число
или, короче, Р(xi).
Число ![]() называется
называется ![]() - той координатой
точки .
- той координатой
точки .
Расстояние
между двумя точками А![]() и В
и В![]() определим по формуле
определим по формуле
![]() (1.1)
(1.1)
Определение 1.2.
Совокупность точек ![]() -мерного пространства, для которых определено расстояние согласно (1.1),
называется
-мерного пространства, для которых определено расстояние согласно (1.1),
называется ![]() -мерным евклидовым
пространством и обозначается
-мерным евклидовым
пространством и обозначается ![]() или
или ![]() .
.
З а м е ч а н и е.
В
случае ![]() получается прямая,
при
получается прямая,
при ![]() - плоскость; при
- плоскость; при ![]() - пространство с
обычным расстоянием и в случае произвольного
- пространство с
обычным расстоянием и в случае произвольного
![]() не нужно искать в
определении какого-то скрытого физического или геометрического смысла. Это есть
просто построение математического аппарата, удобного для изучения функции
многих переменных.
не нужно искать в
определении какого-то скрытого физического или геометрического смысла. Это есть
просто построение математического аппарата, удобного для изучения функции
многих переменных.
Расстояние
между точками в ![]() -мерном евклидовом пространстве обладает следующими свойствами:
-мерном евклидовом пространстве обладает следующими свойствами:
1. ![]() , причем
, причем ![]() .
.
2. ![]() .
.
3. ![]() .
.
Определение 1.3. Пусть каждому натуральному числу ![]() поставлено в
соответствие некоторое вещественное число
поставлено в
соответствие некоторое вещественное число
![]() (причем разным
натуральным числам
(причем разным
натуральным числам ![]() могут соответствовать и одинаковые числа). Совокупность элементов
могут соответствовать и одинаковые числа). Совокупность элементов ![]() называется числовой последовательностью
(или просто последовательностью); каждый элемент
называется числовой последовательностью
(или просто последовательностью); каждый элемент ![]() называется членом
последовательности, а число n - его
номером.
называется членом
последовательности, а число n - его
номером.
Числовую
последовательность ![]() будем обозначать
будем обозначать ![]() , либо
, либо ![]() . Согласно определения, последовательность всегда содержит
бесконечное множество элементов.
. Согласно определения, последовательность всегда содержит
бесконечное множество элементов.
Определение 1.4. Число А называется пределом данной
последовательности ![]() , если
, если ![]() (1.2)
(1.2)
При
этом пишут ![]() или
или ![]() .
.
Отметим, что неравенство (1.2) эквивалентно
![]() (1.2.1)
(1.2.1)
Последовательность, у которой существует предел, называется сходящейся.
Последовательность, не являющаяся сходящейся, называется расходящейся.
Определение 1.5. Для заданного числа х всякий интервал вида ![]() , где
, где ![]() , называется
, называется ![]() - окрестностью (или просто окрестностью) числа (точки) х на числовой прямой и обозначаются
О(х,e).
- окрестностью (или просто окрестностью) числа (точки) х на числовой прямой и обозначаются
О(х,e).
Тогда можно дать другое определение предела.
Определение 1.4.1. Число А называется пределом данной
последовательности ![]() , если в любой его
окрестности содержатся почти все члены
последовательности, т.е. все члены последовательности за исключением их конечного числа.
, если в любой его
окрестности содержатся почти все члены
последовательности, т.е. все члены последовательности за исключением их конечного числа.
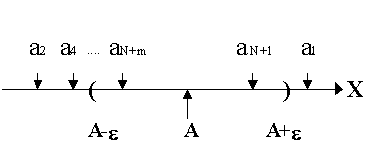
Рис. 1.1.
Следующие утверждения о числовых последовательностях нужно знать и уметь доказывать ( самостоятельно):
1. Сходящаяся последовательность имеет только один предел.
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5.
Если ![]() сходятся и
сходятся и ![]() , то
, то
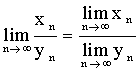 ;
;
1.2. Основные
теоремы для последовательностей
Определение 2.1. Последовательность ![]() называется
ограниченной сверху (снизу), если
существуеттакое число b, что для
любого n an £ b ( an ³ b).
называется
ограниченной сверху (снизу), если
существуеттакое число b, что для
любого n an £ b ( an ³ b).
Определение 2.2. Последовательность ![]() называется монотонно
возрастающей (монотонно убывающей),
если an £ an+1 ( an ³ a n+1).
называется монотонно
возрастающей (монотонно убывающей),
если an £ an+1 ( an ³ a n+1).
Теорема 2.1. (Вейерштрасса). Если последовательность ![]() монотонна и
ограничена, то она имеет предел.
монотонна и
ограничена, то она имеет предел.
Д о к а з а т е л ь с т в о:
Пусть для определенности ![]() - возрастающая и ограничена сверху. Зафиксируем
- возрастающая и ограничена сверху. Зафиксируем ![]() , а так как
, а так как ![]() ограничена, то
ограничена, то ![]() и
и
![]() . Тогда в силу монотонности заданной последовательности
. Тогда в силу монотонности заданной последовательности
![]() в силу (1.2.1)
в силу (1.2.1) ![]() .
.
Поэтому ![]() , что по определению 2.4. означает
, что по определению 2.4. означает ![]() .
.
Аналогично теорема доказывается для
случая, когда ![]() - убывающая и ограничена снизу.
- убывающая и ограничена снизу.
З а м е ч а н и е.
Теорема
Вейерштрасса не имеет места в множестве Q - ![]() рациональные числа
рациональные числа![]() .
.
С л е д с т в и е.
Для того, чтобы монотонно возрастающая (убывающая) последовательность сходилась, необходимо и достаточно, чтобы она была ограничена сверху (снизу).
Это следует из утверждения, что если последовательность имеет предел, то она ограничена , и из теоремы Вейерштрасса.
Теорема 2.2. Если
последовательность ![]() имеет предел, то она
ограничена.
имеет предел, то она
ограничена.
Д о к а з а т е л ь с т в о:
Пусть ![]() , а
, а ![]() Пусть
Пусть ![]() - наибольшее из чисел
- наибольшее из чисел ![]() , т.е.
, т.е. ![]() . По определению 2.6,
. По определению 2.6, ![]() - ограничена.
- ограничена.
Пример 2.1. (Число e.) Пусть
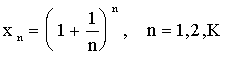
Покажем, что последовательность ![]() сходится.
сходится.
Раскрывая скобки согласно правилу бинома Ньютона, получим
![]()
+ ![]()
=![]() ...+
...+
![]() .
.
При переходе от ![]() к
к ![]() число слагаемых,
которые все положительны,
число слагаемых,
которые все положительны,
возрастает, и кроме того, каждое слагаемое увеличивается:
![]() , то
, то ![]() .
.
Далее, замечая, что каждая из скобок вида ![]() и
и ![]() , получим
, получим
![]() .
.
В левой части неравенства - бесконечно
убывающая геометрическая прогрессия
![]() .
.
Следовательно,
![]() .
.
Но последовательность ![]() монотонно возрастает и
ограничена сверху, а значит, имеет предел, который обозначим буквой е.
монотонно возрастает и
ограничена сверху, а значит, имеет предел, который обозначим буквой е.
З а
м е ч а н и е.
Число e=2,718281828 ... иррационально и трансцендентно, т.е. не является корнем никакого алгебраического уравнения с целыми коэффициентами.
Определение
2.3. Последовательность ![]() удовлетворяет условию
Коши, если
удовлетворяет условию
Коши, если ![]() .
.
Теорема 2.3. (Критерий Коши). Для того, чтобы последовательность сходилась, необходимо и достаточно, чтобы она удовлетворяла условию Коши.
1.3. Сходимость последовательностей
в пространстве
Определение 3.1 Пусть Х
![]()
![]() Rn
Rn![]() и Е
и Е![]() > 0. Множество
всех точек Y
> 0. Множество
всех точек Y ![]()
![]() Rn:
Rn:![]() r
(x,y) < E называется n-мерным шаром с центром в точке Х
радиуса Е или Е-окрестностью.
r
(x,y) < E называется n-мерным шаром с центром в точке Х
радиуса Е или Е-окрестностью.
Будем обозначать это множество
0 (x, Е) = {Y: Y ![]() Rn , r
(x,y) < E };
Rn , r
(x,y) < E };
Для n = 1 0 (х, E) = { Y: ½X - Y½ < E};
n = 2 X(x1, x2); Y(y1, y2);
0 (x, E) = {Y: (y1-x1)![]() - (y2-x2)
- (y2-x2)![]() < E
< E![]() }.
}.
Определение 3.2.
Пусть каждому натуральному числу
m поставлена в соответствие некоторая точка X(m)![]() Rn
(необязательно разные точки
для разных m ). Тогда множество{X(m),
m = 1,2,3,...}, состоящее из точек пространства
Rn с различными
номерами, называется последовательностью точек
в Rn и обозначается
Rn
(необязательно разные точки
для разных m ). Тогда множество{X(m),
m = 1,2,3,...}, состоящее из точек пространства
Rn с различными
номерами, называется последовательностью точек
в Rn и обозначается
Х(m), m = 1,2,3,..., или {x(m)}.
Определение 3.3 Точка Х Î Rn называется пределом последовательности {x(m)} и пишется
![]() , (3.1)
, (3.1)
если ![]() (3.2)
(3.2)
И, если Х = ![]() то будем говорить,
что последовательность {x(m)} cходится к точке Х .
то будем говорить,
что последовательность {x(m)} cходится к точке Х .
Используя понятие окрестности, легко получаем, что
Х
= ![]()
![]()
![]()
![]() E > 0
E > 0 ![]() m
m![]() :
: ![]() m
m ![]()
![]() m
m![]() x
x![]() 0(x,E).
0(x,E).
При n = 1 определение 3.3 превращается в обычное определение предела числовой последовательности.
При n = 2 сходимость последовательности {x(m)} точек плоскости R2 к точке
Х ![]() R2 означает, что каков бы ни был круг с центром
в точке Х, начиная с некоторого номера, зависящего от
радиуса этого круга, все члены данной последовательности лежат в этом круге.
R2 означает, что каков бы ни был круг с центром
в точке Х, начиная с некоторого номера, зависящего от
радиуса этого круга, все члены данной последовательности лежат в этом круге.
В случае n = 3 получаем сходимость в R3. Здесь в роли Е-окрестности выступает шар. А это означает, что каков бы ни был шар с центром в точке Х, начиная с некоторого номера, зависящего от радиуса этого круга, все члены данной последовательности лежат в этом шаре, за исключением их конечного числа.
Понятие предела последовательности {х(m)} точек пространства Rn может быть сведено к понятию предела числовых последовательностей, а именно, последовательностей координат точек х(m), m = 1,2, . . . .
Теорема
3.1 Для того чтобы
последовательность {x![]() }
}
x![]() = (x
= (x![]() , x
, x![]() , x
, x![]() , . . . , x
, . . . , x![]() )
) ![]() Rn, n = 1,2,3, . . . .
Rn, n = 1,2,3, . . . .
сходилась к
точке Х
= (х ![]() , х
, х![]() , х
, х![]() , . . . , х
, . . . , х![]() )
) ![]() Rn
Rn
![]() чтобы
чтобы ![]() , i = 1¸
n.
(3.3)
, i = 1¸
n.
(3.3)
Доказательство этой теоремы будет позже.
1.3.1. Различные типы множеств
Пусть
точка М![]() G, где G - множество, принадлежащее
Rn
G, где G - множество, принадлежащее
Rn
(G ![]() Rn) .
Rn) .
Определение 3.4
Точка M ![]() G называется внутренней точкой этого множества,
если существует
G называется внутренней точкой этого множества,
если существует![]() Е - окрестность этой
точки такой, что O(M; Е)
Е - окрестность этой
точки такой, что O(M; Е) ![]() G.
G.
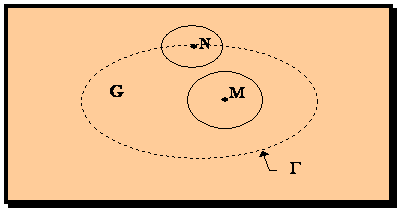
Рис. 3.4
Определение 3.5.
Точка N![]() называется граничной
для множества G , если в любой ее полной окрестности имеются
точки, как
принадлежащие G, так и не принадлежащие
ему.
Сама точка N не обязательно принадлежит G.
называется граничной
для множества G , если в любой ее полной окрестности имеются
точки, как
принадлежащие G, так и не принадлежащие
ему.
Сама точка N не обязательно принадлежит G.
Совокупность всех граничных точек множества G называется его границей ( Г ).
Определение 3.6. Множество G будем называть областью (или открытым множеством), если все его точки внутренние.
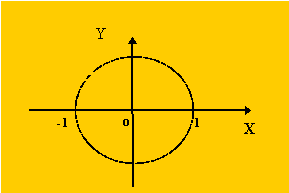 Пример
3.1
Пример
3.1
К = {x, y:
х![]() + y
+ y![]() < 1}
< 1}
Рис. 3.5.
Всякое открытое множество, содержащее точку Х, называется ее окрестностью и обозначается О(х).
Обозначим
![]() = G
= G ![]() Г, тогда множество
Г, тогда множество ![]() будем называть замкнутой областью (замкнутое множество).
будем называть замкнутой областью (замкнутое множество).
Множество S называется связным, если любые две точки этого множества можно соединить непрерывной линией, состоящей из точек данного множества.
Пример 3.2. Пусть Г =
{x, y: x![]() + y
+ y![]() = 1} - граница множества К.
= 1} - граница множества К.
![]() = K
= K ![]() Г = {x, y:
x
Г = {x, y:
x![]() + y
+ y![]()
![]() 1}.
1}.
Определение 3.7. Если
у точки х ![]() А существует окрестность, не
содержащая никаких других точек множества А, кроме
самой точки х, то эта точка называется изолированной точкой
множества.
А существует окрестность, не
содержащая никаких других точек множества А, кроме
самой точки х, то эта точка называется изолированной точкой
множества.
Определение 3.8. Точка х Î Rn называется предельной точкой некоторого множества А Ì Rn, если " 0(х) содержит по крайней мере одну точку множества А, отличную от х.
З а м е ч а н и е. Очевидно, что предельная точка является граничной точкой. С другой стороны, всякая граничная точка множества А является либо ее изолированной точкой, либо предельной.
Пример 3.3. Пусть n=1 E = (0, 1). Тогда каждая точка отрезка [0, 1] является граничной и предельной точкой множества Е, при этом точки {0}, {1} Ï Е.
Пример 3.4. Пусть А = (0,1) È {2}, то точка {2} является изолированной, а Г = [0,1] È {2}.
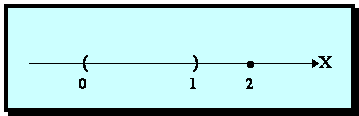
Рис. 3.6.
Определение 3.9. Множество Е Ì Rn называется ограниченным, если существует n-мерный куб Р(0,а) с центром в начале координат 0, такой что E Ì Р(0,а).
З а м е ч а н и е. Всякий n-мерный параллелепипед Р(х,б1, б2 , . . . , бn ) называется прямоугольной окрестностью точки х, если б1=б2=б3 = . . .= бn , то получим n-мерный куб с центром в точке х.
n = 1 Р(х, б) - интервал с центром в точке х.
n = 2 Р(х, б1 , б2 ) - прямоугольник.
n = 3 Р(х, б1 , б2 , б3 ) - n-мерный параллелепипед.
Пусть, например, n = 2 Р(х, б1 , б2 )
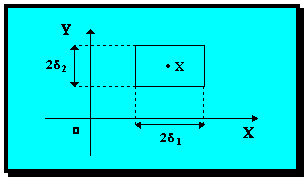
Рис. 3.7.
Теперь проведем доказательство теоремы 3.1.
Теорема 3.1 Для
того чтобы последовательность {x![]() }
}
x![]() = (x
= (x![]() , x
, x![]() , x
, x![]() , . . . , x
, . . . , x![]() )
) ![]() Rn, n = 1,2,3, . . . .
Rn, n = 1,2,3, . . . .
сходилась к
точке Х
= (х ![]() , х
, х![]() , х
, х![]() , . . . , х
, . . . , х![]() )
) ![]() Rn
Rn
необходимо и достаточно
чтобы ![]() , (i = 1¸ n). (3.3)
, (i = 1¸ n). (3.3)
Д о к а з а т е л ь с т в о :
а). Необходимость условия 3.3.
Пусть ![]() = x.
= x.
Зафиксируем Е > 0,
тогда $ m![]() :
:
x![]() Î
P(x, E)
, " m ³ m
Î
P(x, E)
, " m ³ m![]() , т.е.
, т.е.
çx![]() - xi ç < E, "i
= 1, 2, . . . , n и при m ³
m
- xi ç < E, "i
= 1, 2, . . . , n и при m ³
m![]() , а это и означает, что
, а это и означает, что
![]() = xi , i = 1, 2, . . . , n.
= xi , i = 1, 2, . . . , n.
б). Достаточность условия 3.3.
Пусть ![]() = xi
, i = 1, 2, . . . ., n, и
Р(x, E1 , E2 , . . . , En )
-заданная прямоугольная окрестность точки
х. Тогда для каждого Еi > 0
= xi
, i = 1, 2, . . . ., n, и
Р(x, E1 , E2 , . . . , En )
-заданная прямоугольная окрестность точки
х. Тогда для каждого Еi > 0
i= 1, 2, . . . , n $ mi = m(E): " m ³ mi будет выполнено
çxi(m) - xi ç < Ei (i = 1, 2, . . . , n).
Обозначим m![]() = max {m1 ,
m2 , . . . , mn },
= max {m1 ,
m2 , . . . , mn },
Теперь при m ³ m![]() и "i = 1, 2, . . . , n будет выполнено условие
и "i = 1, 2, . . . , n будет выполнено условие
çxi(m) - xi ç < Ei , i = 1, 2, .![]() . . , n, и при m ³
m
. . , n, и при m ³
m![]()
![]() будем иметь
будем иметь
х Î Р(x, E1
, E2 , . . . , En ),
что и означает ![]() .
.![]()