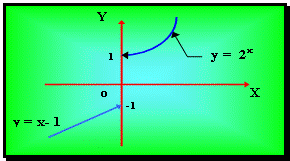
2. Функция
2.1. Понятие функции
Пусть заданы два множества Х и Y. Если
каждому элементу х![]() Х поставлен в соответствие один и только один элемент у
Х поставлен в соответствие один и только один элемент у ![]()
![]() У , обозначаемый f(х), и если каждый элемент у
У , обозначаемый f(х), и если каждый элемент у![]() У при этом оказывается поставлен в соответствие хотя бы
одному элементу х
У при этом оказывается поставлен в соответствие хотя бы
одному элементу х![]() Х, то говорится, что на множестве Х задана однозначная
функция у = f(х). Множество Х называется областью ее определения, а множество Y - множество ее значений. Элемент х
Х, то говорится, что на множестве Х задана однозначная
функция у = f(х). Множество Х называется областью ее определения, а множество Y - множество ее значений. Элемент х![]() Х называется аргументом или независимой переменной,
а элементы у
Х называется аргументом или независимой переменной,
а элементы у![]() Y - значениями функции,
или зависимой переменной..
Y - значениями функции,
или зависимой переменной..
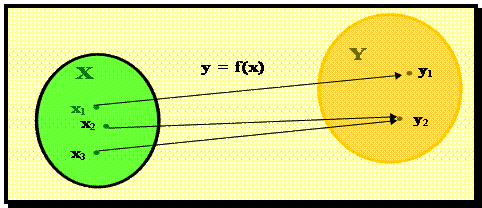
Рис.
2.1.
Элементы
х и у рассматриваемых множеств могут иметь совершенно произвольную природу.
Если значениями функции являются не числа, а другие элементы, часто вместо
слова “функция” употребляют слово “отображение”.
Для
того, чтобы задать функцию f, надо знать:
1.
Х - область определения (существования);
2.
Y - область значений;
3. Закон соответствия, по которому определяется
элемент у![]() Y, соответствующий х
Y, соответствующий х![]() Х.
Х.
Пример 2.1. Вещественные, комплекснозначные
и другие функции.
Пусть {xn}-
последовательность, тогда хn=f(n).
D(f)
= N; xn![]() Rn.
Rn.
Над
функциями, принимающими числовые значения (числовые функции), можно производить
арифметические операции.
Пусть
f и g -
числовые функции, определенные на одном и том же множестве Х, а с -
const и у = f(x), то
![]() ;
;
![]() ;
;
![]() ;
;
Если ![]() ,
, ![]()
![]() ;
;
Выражения
в правой части понимаются как функция, принимающая в каждой точке х![]() значения:
значения: 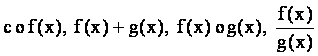 .
.
Определение
2.1. Функция f
ограничена на множестве Х ![]() M > 0 :
M > 0 :
![]() .
.
Т.е.
если ![]() , где
, где ![]()
а) ![]() - ограничена сверху;
- ограничена сверху;
б) ![]() - ограничена
снизу.
- ограничена
снизу.
Будем
говорить, что числовая функция f, определенная на множестве Х, принимает в
точке ![]() наибольшее значение (наименьшее),
если
наибольшее значение (наименьшее),
если ![]() и будем писать
и будем писать
![]() .
.
Иногда
приходится иметь дело с ![]() , определенными на Х,
значениями которых являются некоторые подмножества множества Y, т.е. каждому элементу
, определенными на Х,
значениями которых являются некоторые подмножества множества Y, т.е. каждому элементу ![]() ставится в
соответствие некоторое множество
ставится в
соответствие некоторое множество ![]() и тем самым множество
значений функции является совокупностью
некоторых подмножеств множества Y. B этом случае говорят, что на множестве Х задана многозначная
функция
и тем самым множество
значений функции является совокупностью
некоторых подмножеств множества Y. B этом случае говорят, что на множестве Х задана многозначная
функция ![]() со значениями во
множестве Y.
со значениями во
множестве Y.
Определение
2.2.
Пусть ![]() и Y - множество ее
значений. Обозначим
и Y - множество ее
значений. Обозначим ![]() - полный прообраз элемента
- полный прообраз элемента ![]() , т.е.
, т.е. ![]() . Тогда функция, определенная на Y и ставящая в соответствие
каждому
. Тогда функция, определенная на Y и ставящая в соответствие
каждому ![]() множество
множество ![]() , называется обратной к
, называется обратной к ![]() и обозначается
и обозначается ![]() .
.
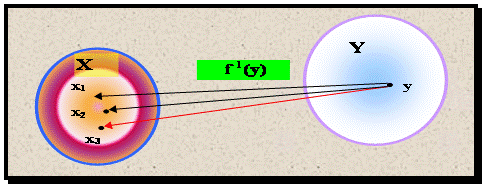
Рис.
2.2.
2.2. Способы задания функций.
1. Если функция задана выражением при помощи
формулы, то говорят, что она задана аналитически, Для этого используется
некоторый запас изученных и специально обозначенных функций, алгебраические
действия и предельный переход.
Например,
![]() .
.
Здесь ![]() - это совокупность
действий, которые нужно выполнить в определенном порядке над значениями
аргумента х, чтобы получить соответствующее значение функции y
(или, то же самое,
- это совокупность
действий, которые нужно выполнить в определенном порядке над значениями
аргумента х, чтобы получить соответствующее значение функции y
(или, то же самое, ![]() ).
).
Примеры:
1.
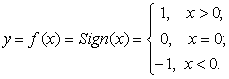
2. Функция Дирихле:
![]()
3.
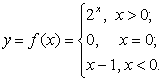
2. Функцию можно задавать таблично,
т.е. для некоторых значений х указать соответствующие значения переменной y.
|
X |
x1 |
x2 |
... |
xi |
... |
xn |
|
Y |
y1 |
y2 |
... |
yi |
... |
yn |
Данные такой таблицы могут быть получены как экспериментально,
так и с помощью математических расчетов.
Примерами табличного задания функций могут быть:
логарифмические таблицы, таблицы тригонометрических функций.
3. Аналитический и табличный способы задания функций
страдают отсутствием наглядности.
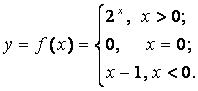 (*)
(*)
|
Рис. 2.3. |
Графический способ
задания функции - это геометрическое место точек на плоскости с координатами ![]() .
.
Рассмотрим пример (*), тогда ее грфическ Рис. 2..3.
2.3. Понятие функции
нескольких переменных.
Рассмотрим
вещественные функции, определенные на множестве ![]() -мерного евклидового пространства Rn, значениями
которого являются вещественные числа.
-мерного евклидового пространства Rn, значениями
которого являются вещественные числа.
Эти
функции обозначаются одним символом, например, ![]() или указывая аргумент
-
или указывая аргумент
- ![]() , или
, или ![]() и называются функциями
многих переменных. Здесь переменные
и называются функциями
многих переменных. Здесь переменные ![]() называются
независимыми переменными или аргументами. Совокупность рассматриваемых их
значений - областью определения
(областью существования).
называются
независимыми переменными или аргументами. Совокупность рассматриваемых их
значений - областью определения
(областью существования).
Областью
существования функции двух переменных (х и y), вообще говоря, представляет
собой некоторое множество точек плоскости Oxy, т.е.
![]() .
.
Аналогично
![]() для
для ![]() =3.
=3.
2.4. Неявные функции
( Один из способов задания
функции )
Определение
2.3.
Функция у от аргумента х называется неявной,
если она задана уравнением вида: F(x,y) = 0, (4.1)
т.е. задана
функция F(x,y) двух вещественных
аргументов x и y (если они существуют), для которых выполняется (4.1).
Чтобы выразить
функцию y в явном виде, достаточно разрешить (4.1) относительно y. Так как для данного значения аргумента х уравнение
(4.1) может иметь несколько (и даже
бесконечное множество) корней y, то в общем случае неявная функция является
многозначной.
Например, функция у (у>0), определяемая
уравнением![]() , является неявной. Явно заданная функция будет иметь вид:
, является неявной. Явно заданная функция будет иметь вид: ![]() .
.
2.5. Сложные функции
( Один из способов задания функции )
Пусть
заданы две функции ![]() ,
, ![]() , причем область задания функции F содержит область значений
функции
, причем область задания функции F содержит область значений
функции ![]() , тогда
, тогда ![]() из этой области
определения
из этой области
определения ![]() ставится в
соответствие
ставится в
соответствие ![]() , где
, где ![]() . Эта функция, определенная соответствием
. Эта функция, определенная соответствием ![]() , называется сложной функцией, или суперпозицией функций
, называется сложной функцией, или суперпозицией функций ![]() и F.
и F.
Примеры:
1.  ;
;
2. ![]() .
.
![]() - явно задана.
- явно задана.
2.6. Элементарные функции и
их классификация
Функции:
![]() - степенная;
- степенная;
![]() - показательная;
- показательная;
![]() -
логарифмическая;
-
логарифмическая;
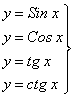 - тригонометрические;
- тригонометрические;
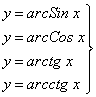 - обратные
тригонометрические;
- обратные
тригонометрические;
![]() - постоянная.
- постоянная.
Называются основными элементарными функциями.
З а м е ч а н
и е.
Всякая
функция, которая может быть явным образом задана с помощью формулы, содержащей
лишь конечное число арифметических операций и суперпозиций основных
элементарных функций, называется просто
элементарной функцией.
Элементарные
функции обычно делят на классы:
1. Многочлены (полиномы) - это функции
вида:
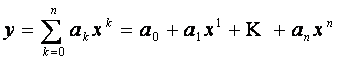 .
.
Если ![]() , то число
, то число ![]() называется степенью
данного полинома.
называется степенью
данного полинома.
При ![]() многочлен первой
степени и называется линейной функцией;
многочлен первой
степени и называется линейной функцией;
2.
Класс рациональных функций:
![]() , где
, где ![]() - полиномы;
- полиномы;
3. Алгебраические функции:
Функции, заданные с помощью суперпозиций
рациональных функций, степенных с рациональными показателями и четырех
арифметических действий, называются алгебраическими.
Например:
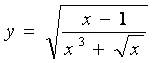 .
.
2.7. Трансцендентные функции.
Элементарные
функции, не являющиеся алгебраическими, называются трансцендентными элементарными функциями.
Функции
вида:
![]() -
показательная;
-
показательная;
![]() - логарифмическая;
- логарифмическая;
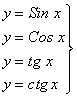 -
тригонометрические;
-
тригонометрические;
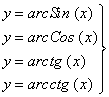 - обратные
тригонометрические).
- обратные
тригонометрические).
Самостоятельно.
1. Графики основных
элементарных функций;
2. Свойства функций
(нечетность, четность, периодичность).
3. Предел функции
3.1. Определение предела
функции
Определение
3.1.
Пусть функция f(х) определена на некотором интервале (а,в), кроме, быть может, точки хо Î( а, в ). Число А называется
пределом функции f(х) в точке
хо, т.е.
![]() ,
,
если " e > 0 $ d
= d(e) > 0: "х Î ( а, в), удовлетворяющих условию
çх - хоç < d, х ¹ хо ![]() (3.1)
(3.1)
çf(x) - Aç < e.
(3.2)
|
Рис. 3.1. |
Таким образом, число
А называется пределом
функции f(х) в точке хо A = ![]() , при х ® хо тогда и только тогда, когда для любого (") e > 0 существует ( $) такая дельта окрестность d = d (e) > 0 точки хо :
, при х ® хо тогда и только тогда, когда для любого (") e > 0 существует ( $) такая дельта окрестность d = d (e) > 0 точки хо :
"х Î (а, в) : х Î O ( хо
, d), х ¹ хо Þ f ( x ) Î O ( A, e ).
З а м е ч а н
и е. Понятие предела, естественно, переносится
на функции нескольких переменных.
Пусть
f (х, у) - функция двух переменных, заданная на
множество Х плоскости Оху.
Под
окрестностью Оа,в точки
Мо (а, в) (а
и в - конечные)
будем понимать внутренность любого прямоугольника {a1 < х < b1 , a2 < у
< b2 },![]() построенного вокруг
точки Мо (т.е. a1 < а < b1 , a2 < в < b2 ), из
которого удалена сама точка Мо.
построенного вокруг
точки Мо (т.е. a1 < а < b1 , a2 < в < b2 ), из
которого удалена сама точка Мо.
В
таком утверждении можно записать 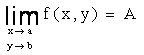
" e > o $ Oа,в : " M (х ,у ) Î Oа,в Þ ç f (x, y) - A ç < e.
При
этом предполагается, что в любой Оа,в $ M (х,у ), в
которых f (х, у) имеет смысл (предельная
точка).
3.2. Односторонние пределы функции
Введем
понятие левой и правой окрестности точки
хо - число.
Определение
3.2.
Любой интервал ![]() = (a, xo) ((
= (a, xo) ((![]() = (xо, b )), правым (левым) концом
которого является точка хо,
назовем ее левой (правой) окрестностью.
= (xо, b )), правым (левым) концом
которого является точка хо,
назовем ее левой (правой) окрестностью.
Символически
факт, что х принимает лишь значения, принадлежащие
некоторой левой окрестности точки хо, будем обозначать
х ® хо - 0,
х < хо.
Аналогично х ® хо + 0 , х > хо .
Определение 3.3. Число А называется пределом
функции слева, если
" e > 0 $ ![]() : " х Î CÇ
: " х Î CÇ![]() Þ çf( x) - A ç < e.
Þ çf( x) - A ç < e.
И будем писать![]() , где Х - область
определения f (х).
, где Х - область
определения f (х).
Аналогично
![]() - предел функции
справа.
- предел функции
справа.
З а м е ч а н и е.
Можно, конечно, ограничиться
рассмотрением левых d - окрестностей точки хо :![]() = (хо - d, хо
) , где
d = d ( e ) > 0.
= (хо - d, хо
) , где
d = d ( e ) > 0.
![]() = (xo
, xo + d), где
d = d ( e ) > 0.
= (xo
, xo + d), где
d = d ( e ) > 0.
O(xо - 0, d ) = {
х: хо - d
< x £ хо
}, d > 0
O(х + 0, d ) = {х : хо
£ х
< xo + d }, d > 0.
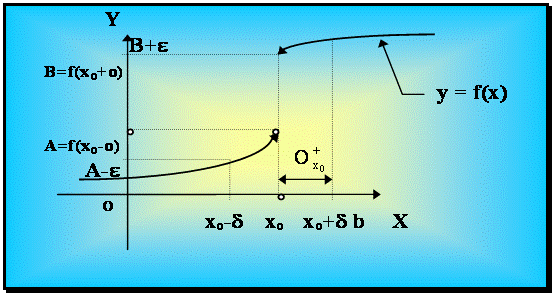
Рис.3.2.
Пример 3.1.
Пусть f(х) = sgnх = ![]() ,
,
Опредеена для вех x ¹ 0.
Здесь ![]() , а
, а ![]() .
.
Теорема 3.1. Для существования предела
функции f(х) при х ® хо (хо
- число)
Û f(хо - о) = f(хо
+ о).
Д о к а з а т е л ь с т в о: Пусть
![]() ,
,
тогда " e > о $ d = d(e) > о: çх -хоç< d = > çf (х) ¹ A ç < e,
и следовательно $ ![]() = (хо
- d, хо)
и
= (хо
- d, хо)
и ![]() = ( xо
, xо + d ) :
= ( xо
, xо + d ) :
А = ![]() и А =
и А = ![]() .
.
Обратно,
если существуют пределы А =![]()
![]() f(x) и А =
f(x) и А = ![]() , то " e > 0 $ d1 = d1 (e) и d2 = d2 (e) такие, что, если
, то " e > 0 $ d1 = d1 (e) и d2 = d2 (e) такие, что, если
хо - d1 < х < хо и,
соответственно, хо <
х < xо + d2 Þ
çf(х) - Aç < e
Возьмем d = min {d1, d2} Þ çf( x ) - A ½< e при çх -хоç< d,
х ¹ хо. И
тогда, согласно определения 3.1![]()
![]() .
.
Лемма 3.1.
Если f(х) имеет
предел в точке хо, то
существует окрестность этой точки (быть может,
выброшенной точкой хо),
на которой функция ограничена.
Теорема 3.2. (Правило
замены переменного для пределов функции)
Пусть
существуют ![]() o, f(х) ¹ уо " х ¹ хо и
o, f(х) ¹ уо " х ¹ хо и ![]() Þ при х ® хо существует предел сложной функции
F[f(x)] и
Þ при х ® хо существует предел сложной функции
F[f(x)] и
![]()
![]()
3.3. Свойства пределов функции
Пусть
все функции, рассматриваемые ниже, определены на (а, в), кроме, быть
может, фиксированной точки хо
Î (а, в), тогда верны следующие
свойства:
1. Если j ( х ) £ ¦ ( х) £ y ( х )
и
А = ![]() =
= ![]() Þ
Þ ![]() = A.
= A.
2. Если ¦(х) = С (сonst) Þ ![]() ¦(x) = C .
¦(x) = C .
3. Если ![]() cущ. Þ"с - const
cущ. Þ"с - const
![]()
![]()
4. Если существуют конечные пределы ![]() и
и ![]() , тогда:
, тогда:
а) ![]()
![]()
![]() ;
;
б) ![]() ;
;
в) ![]() =
=  .
.
Все
эти свойства доказываются одинаковым методом, основанным на соответствующих
свойствах пределов
последовательностей. Для
доказательства этих свойств введем понятие бесконечно малых и бесконечно
больших функций.
3.4. Бесконечно малые и
бесконечно большие функции
Определение 3.4. Функция a = a(х) называется бесконечно малой функцией (или просто бесконечно малой) при х ® хo, если ![]()
Лемма 3.2. Предел ![]() существует и
равен А Û ¦ (х) = A + a (х),
существует и
равен А Û ¦ (х) = A + a (х),
где a (х) - бесконечно малая.
Д о
к а з а т е л ь с т в о: Пусть ![]() , то, полагая ¦(х) - A = a (х),
получим
, то, полагая ¦(х) - A = a (х),
получим ![]() .
.
обратно, если
¦(х) = A + a(х) и ![]() .
.
Из
леммы 3.2. следует, что если ![]() , то в некоторой
окрестности Охо знак f(х)
(х Î C) совпадает
со знаком числа А.
, то в некоторой
окрестности Охо знак f(х)
(х Î C) совпадает
со знаком числа А.
Определение
3.5. Функция
f = f(x) называется бесконечно большой при х ® хо, если "e > 0 $ d = d (e) > 0: ç¦(x)ç > e, "x : çx -xoç< d, x < xo. В этом случае будем писать ![]() .
.
Если "e > 0 $ d : ¦(х) > e ( ¦(х) < - e) "х : çх-хо ç < d,
х ¹ хо Þ ![]() , (
, ( ![]() ).
).
По
аналогии с конечными односторонними пределами определяются односторонние
бесконечные пределы ![]() ,
, ![]() .
.
З а м е ч а н
и е. Величина, обратная бесконечно малой,
является бесконечно большой.
Пусть a = a (х), a (х) ¹ 0
при х ¹ хо есть
в бесконечно малой (или бесконечно большой) тогда
![]() бесконечно большая
(бесконечно малая).
бесконечно большая
(бесконечно малая).
В
дальнейшем будем использовать символические записи для любого числа а>0 :![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Рассмотрим свойства бесконечно малых функций.
1) Алгебраическая сумма
конечного числа бесконечно малых, определенная на общем множестве, есть величина бесконечно
малая при х ® хо.
2) Произведение ограниченной при х ® хо функции на бесконечно малых есть функция
бесконечно малая.
2") Произведение конечного числа бесконечно
малого при х ® хо есть функция бесконечно малая.
3) [a( х ) ]n - ( n - целая положительная степень) a (х) - бесконечно малая тогда и
[a (х) ]n - бесконечно малая.
4) Что касается отношения двух бесконечно малых
![]() ,
, ![]()
![]() - может быть функция произвольного поведения.
- может быть функция произвольного поведения.
Но с помощью
действия деления можно сравнить между собой бесконечно малые.
Определение
3.6. a (х), b (х)
бесконечно малые при х ® хо имеют одинаковый порядок, если их отношение
имеет конечный предел, отличный от нуля,
т.е.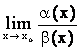 =K¹ 0.
=K¹ 0.
Определение
3.7.
Порядок бесконечно малой b (х) выше
порядка бесконечно малой a(х), если отношение ![]() есть бесконечно
малое при х ® хо, т.е.
есть бесконечно
малое при х ® хо, т.е. ![]() = 0.
= 0.
В этом
случае пишут b(х) = 0 [a (х)] при
х ® хо
.
Определение
3.8.
Бесконечно малая b (х) имеет предел
n относительно бесконечно малой a (х)
при х ® хо, если
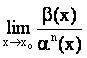 = K ¹ 0.
= K ¹ 0.
Докажем
одно из свойств сформулированных в1.5.3., например, свойство
4. Если существуют конечные пределы ![]() и
и ![]() , тогда:
, тогда:
![]()
Д о к а з а т е л ь с т в о: Пусть
![]() ,
, ![]()
Тогда имеем на основании 3.2. ¦(х) = A + a (х), g(х) = B + b(х), где a(х), b(х) - бесконечно малые при х ® хо
Тогда ¦(х) × g(х) = A × B + g(х), где g(х) = A × b (х) + b × a) + a (х) × b(х) -
есть бесконечно малая Þ g(х) ® 0 бесконечно
малая на основании свойств бесконечно малой функции.
Отсюда
![]() .
.
Рассмотрим
в качестве примера предел отношения синуса бесконечно малой дуги к самой дуге.
Теорема.(Первый
замечательный предел). Предел отношения синуса бесконечно малой дуги к
самой дуге, выраженной в радианах, равен
единице, 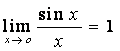 .
.
Д о к а з а т е л ь с т в о:
Пусть х > 0
и х ® 0,
так что 0 <
х < ![]() .
.
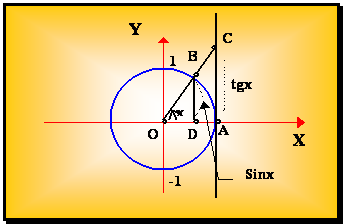
Рис.3.4.
В
тригонометрическом круге R = 1 рассмотрим
S DОАВ, S
cек. ОАВ, SDОАВ
SDОАВ =  SDОАВ =
SDОАВ = 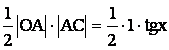
Получаем ![]()
т.е. Sin x
< x < tg x разделим на Sin x > 0, получим
1 < ![]() или cos x <
или cos x < ![]() .
.
Пусть теперь
х ® 0 +
0, но
![]()
т.к. 1 -
cos x = 2 sin2![]() бесконечно малая по
условию,
бесконечно малая по
условию,
то ![]() . Тогда функция
. Тогда функция ![]() заключена между двумя функциями, имеющими предел, равный 1.
заключена между двумя функциями, имеющими предел, равный 1.
На
основании свойства 1, получаем ![]() .
.
Если х < 0 ;
имеем ![]() , где - х > 0.
, где - х > 0.
Поэтому 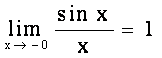 .
.
З а м е ч а н
и е. " х çsin x ç £ çx ç,
причем равенство имеет место при
х = 0.
Второй замечательный
предел. (Число е).
Ранее было доказано, что последовательность ![]() имеет предел, заключенный между 2 и 3.
имеет предел, заключенный между 2 и 3.
Можно доказать, что функция у =  , х Î (-¥, -1) È (0, +¥)
при х ® ¥ стремится к
е:
, х Î (-¥, -1) È (0, +¥)
при х ® ¥ стремится к
е:
е = 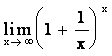 .
.
Пусть ![]() , тогда e =
, тогда e = 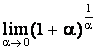 или
или 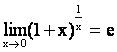 ,
,
где е = 2,7182818284... .
Пример практического применения понятия
предела функции в экономических расчетах