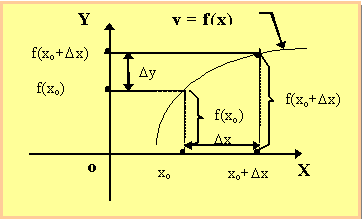
4. Непрерывность функции в точке

 

4.1. Точки непрерывности и точки разрыва функции

 

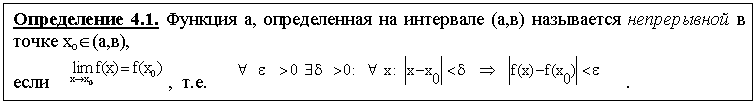
Подпись: Определение 4.1. Функция а, определенная на интервале (а,в) называется непрерывной в точке хоÎ(а,в), если , т.е. .

 


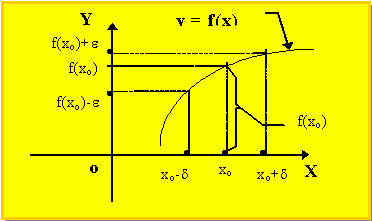
Рис.4.1.

 

 

Или, если ввести следующие обозначения :

  Dx = x0  -  x,   Dy = f(x) - f(x0)

Dx - приращение аргумента;

Dy - приращение функции.

         Пусть  y = f(x),

где х - текущая точка из области определения.

 

 

                                        Рис.4.2.

 

Подпись: Определение 4.2. Функция f(x), определенная на Х, называется непрерывной в точке х = хо (хоÎХ). 1) функция в этой точке определена; 2) при Dх = хо - х ® 0 и , т.е. функция называется непрерывной в данной точке, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. f(x) - непрерывна в точке х0 Û " e>0 $ d>0 : çx-x0ç<d , т.е. 0<çDx ç<d , çf(x)-f(x0)ç=çf(x0+Dx)-f(x0)½<e.

 

Подпись: Определение 4.3. Функция называется непрерывной на данном множестве Х, если 1) она определена на этом множестве, т.е. " х Î Х $ f(x) ; 2) непрерывна в каждой точке этого множества, т.е. " х Î Х справедливо .

 

 

        

 

 

 

 

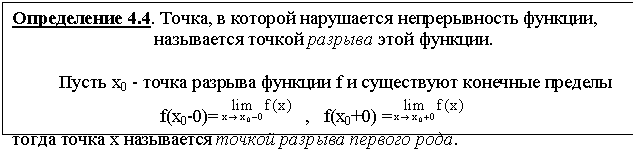
Подпись: Определение 4.4. Точка, в которой нарушается непрерывность функции, называется точкой разрыва этой функции. Пусть х0 - точка разрыва функции f и существуют конечные пределы f(x0-0)= , f(x0+0) = тогда точка х называется точкой разрыва первого рода.

 

 

 

 

 

 

 

Величина f(x0+0) - f(x0-0) называется скачком функции f в точке х.

         Если f(x0-0)=f(x0+0), то х называется точкой устранимого разрыва.

         Если доопределить функцию таким образом, что

         f(x0)==, то получим непрерывную функцию.

         Точка разрыва, не являющаяся точкой разрыва первого рода, называется точкой разрыва второго рода. Таким образом, в точках второго рода по крайней мере один из пределов не существует 

   ,.

 Примеры: Различные разрывы функции в точке представлены ниже.

 

 

 

 

 

 

 

 

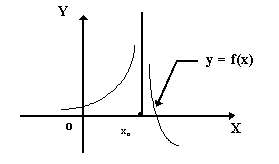
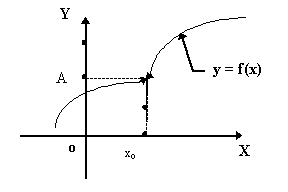
Рис.4.3

 

 

4.2. Основные теоремы о непрерывных функциях

 

Теорема 4.1. Сумма конечного числа непрерывных функций, определенных на некотором множестве Х, есть функция непрерывная.

 

Теорема 4.2. Произведение конечного числа непрерывных функций есть функция непрерывная.

 С л е д с т в и е. Целый полином    Р(х)=а0+а1х+... +аnхn  есть функция непрерывная.

 

Теорема 4.3. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, в которых делитель отличен от нуля.

 

Теорема 4.4. Непрерывная функция от непрерывной функции есть функция непрерывная.

 

Теорема 4.5. Если y = f(x) непрерывна и строго монотонна на промежутке <а,b> ,  то существует обратная функция х = j(y), определенная на промежутке < f(a), f(b) >, причем последняя также монотонна и непрерывна в том же смысле.

 

         В качестве упражнения теоремы 4.1. - 4.5. - доказать самостоятельно.

 

Пример.  Рассмотреть обратные функции к данным:

                   а)   ;    б)  .

 

         Рассмотрим теперь непрерывность функции на множествах.

 

Подпись: Определение 4.5. Пусть f определена на множестве Е Ì Rn . Функция f называется непрерывной в точке х(0) Î Е, если " e>0 $ d=d(e) : " х Î Х , удовлетворяющих условию r(х, х(0)) < d выполняется неравенство çf(x)- f(x(0)) ç < e .

         Примем без доказательства ряд простых, но важных теорем.

 

Теорема 4.6. (Кантора) Функция, непрерывная на ограниченном замкнутом множестве, является равномерно непрерывной.

 

Подпись: Определение 4.6. Функция у = f(х), определенная на множестве Е Ì Rn называется равномерно непрерывной на Е, если " e > 0 $ d = d(e)>0 : " x/, x// Î E удовлетворяющих условию r(x/,x//)<d будет выполнено неравенство çf(x/) - f(x//) ç< e .

Теорема 4.7. (Вейерштрасса) Всякая непрерывная на отрезке функция имеет на этом отрезке как наибольшее, так и наименьшее значение.

 

Теорема 4.8. (Коши) Если f - непрерывна на [a, b] и f(b)  = A, f(b) = B, то

"    A < C < B    $   x Î [a, b]  :   f(x) = C.

 

 

С л е д с т в и е. Если f - непрерывна на [a, b], а на концах отрезка принимает значения переменных знаков (является знакопеременной), то  $   точка

х0 Î [a,b]  :    f(x0) = 0.      

 

5.  Дифференциальное исчисление функции одной переменной

 

5.1. Производная функции в точке

 

Подпись: Определение 5.1. Пусть y = f(x) определена в некоторой точке О(х0) и пусть х - такая точка : х Î О(х0) х ¹ х0 . Если отношение имеет предел при х ® х0 , то этот предел называется производной функции в точке х0 и обозначается f/(x0).

         Таким образом,

                             f/(x0) = .                                                   (5.1)

         Если использовать обозначения Dх = х - х0 и Dу = f(Dx+x0) - f(x0), тогда (5.1) запишем

                                       y/=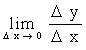.                                                          (5.2)

         Если для некоторого значения х0 выполняется условие

 = ±¥ ,

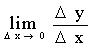 то говорят, что для этого значения существует бесконечная производная.

 

Подпись: Определение 5.2. Если f определена в односторонней области правой, (левой) точки х0 и существует конечный или бесконечный предел , , то о называется производной справа, (слева) и обозначается f+/(x0), (f-/(x0)).

         Операция вычисления производной от данной функции называется операцией дифференцирования.

 

 Примеры :

         1. y = c (c - const),   т.к.  Dy = c - c = 0,  то  = 0 = с/ .

         2. y = Sin x, (самостоятельно);

         3. y = Cos x, (самостоятельно);

 

          4. y = ax

        Пусть необходимо определить y/ = (ax)/ = .

         Dy =  ax+Dx - ax  =  ax(aDx - 1), тогда

     и   .

         Докажем, что

                                                                                                (5.3)

         Функция у = ах - 1 строго монотонна и непрерывна

    "  хÎ (-¥ ,+¥ ) , поэтому обратная функция х =   так же монотонна и непрерывна при у > -1.

При х = 0  Þ  у = 0 , тогда условия х ® 0 и у ® 0 эквивалентны. Сделаем замену переменных в (5.3)

              .

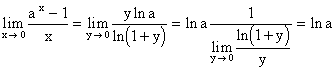Следовательно,

    (ах)/  =  ах ln a, если а = е Þ  (ех)/  =  ех ln е , т.е. показательная функция с основанием е имеет производную, совпадающую с самой функцией.

 

         5.  у = хn , n - положительное целое.

                   Используем разложение бинома :

           и, следовательно,

 

при  Dх ® 0 получим, что

               :

                       (xn)/ = n xn-1 .

         В дальнейшем мы увидим, что эта формула справедлива, если n - вещественное число.

 

Подпись: Теорема 5.1. Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна. Обратное утверждение неверно : непрерывная функция может и не иметь производной.

 Д о к а з а т е л ь с т в о :

         Пусть y = f(x) дифференцируема в точке х, т.е.

Dу=Dx     ( Dx¹0 ).

         Отсюда

=y/ 0=0 .

         Следовательно, функция y = f(x) непрерывна в точке х.

 

6. Дифференциал функции

 

Подпись: Определение 6.1. Пусть y=f(x) определена в некоторой окрестности точки х0 и пусть Dх=х-х0 . Функция f называется дифференцированной в точке х0 , если приращение Dу= f(Dx+x0)-f(x0) представимо в виде Ay = A Dх + a(Dх), (6.1) где А - const, a(Dх) = O(Dх) при Dх® 0.

         Линейная функция A Dх  от ( Dх ) называется дифференциалом функции f в точке х0  и обозначается df(х0 ) или dy. 

 

         Таким образом,

                                      Dу= dy+ O(Dх) при Dх® 0.                                      (6.2)

                                                                            dy = A Dх.                             (6.3)

З а м е ч а н и е. Дифференциал функции dy= A Dх определен для

" Dх Î ( -¥, +¥ ), в то время как приращение функции Dу=f(Dx+x0)-f(x0) можно рассматривать только для таких Dx, для которых  Dx+x0  Î Х.

( Х -  область определения функции f).

         Пусть b - бесконечно малая при  х ® x0 , если  b представима в виде b =a + O(a), где a - бесконечно малая при х ® x0 , то бесконечно малая  a называется главной частью бесконечно малой b.

         Итак, если f(x) дифференцируема в точке x0 , то с точностью до бесконечно малых более высокого порядка, чем х-х0 , она равна линейной функции; иначе говоря, в этом случае функция f в окрестности точки x0 ведет себя “почти как линейная функция”

                                 у0+А(x+x0),                                                                       (6.4)

причем погрешность при замене функции f линейной функцией (6.4) будет тем меньше, чем меньше разность х-х0 , и более того, отношение этой погрешности к разности х-х0  стремится к нулю при х ® x0 .

         Для большей симметрии записи дифференциала переменную  Dx обозначим dx и назовем дифференциалом независимого переменного.

 

Тогда

                                                   dy=A dx.

         Если функция дифференцируема в каждой точке некоторого интервала, то ее дифференциал является функцией двух переменных - точки х и переменной dx :               dy=A(x) dx.

Пример:

      Пусть у = х3 , тогда

                   

главная часть при  Dх ® 0  равна 3х2 Dх, поэтому  dy=3х2 dx.

 

         Теперь установим связь между дифференцируемостью функции в точке и ее производной в той же точке.

 

Подпись: Теорема 6.2. Для дифференцируемости функции f в точке x0 необходимо и достаточно чтобы она имела производную в этой точке, тогда в этом случае dy=f/(х)dx.

 

Д о к а з а т е л ь с т в о:  (необходимость).

 

         Пусть f дифференцируема в точке x0  , т.е.

 Dy = A Dх+ О(Dх)

тогда

                                     =А+ =A.

          Поэтому производная f/(x0) существует и равна А. Отсюда    dy=f/(x0) dx.

 

(достаточность)

         Пусть существует производная, т.е. существует

             = f/(x0) + e(Dх) , где

 И тогда "  Dx ¹ 0

                                                 Dy= f/(x0) + e(Dх)×Dх                                         (6.5)

 И так как   e(Dх)×Dх=О(Dх), то наличие равенства (6.5) означает дифференцируемость.

 

         Из доказанного следует, что А - коэффициент в определении дифференциала - определен однозначно.

         Из формулы (6.5) получаем новое обозначение для производной

                                           у/ = .

Примеры :

                  dС = 0,                          (С - Сonst);

                  dSin(x) = Cos(x)dx;

                  dCos(x) = -Sin(x)dx;

                  dax=ax lna dx,   (dex=ex dx );

                  dxn=n xn-1 dx,             ( n - положительное  число ).

 

Назад  Далее