7. Геометрический
смысл производной и дифференциала
Понятие производной и дифференциала функции в данной точке связано с понятием касательной в этой точке.
Пусть y = ¦(х) определена на интервале (a, b) и непрерывна в точке
хо Î (а, в) и пусть уо = f (хо). Введем в рассмотрение точки:
Мо(хо, уо), хо + h Î (а, в) ; Мh (хо + h, f(х о + h)).
|
Рис. 7.1. |
Проведем секущую Мо Мh, тогда уравнение прямой, проходящей через две данные точки, можно записать
у =
К(h) (х - хо) + уо
,
где![]()
![]()
![]() (7.1)
(7.1)
Покажем, что при h ® 0 расстояние r (Mо, Mh) ® 0, в этом случае будем говорить, что точка Мh ®Mо. Действительно, в точке хо функция f - непрерывна, следовательно,
![]() , а
, а ![]()
В силу равенства (7.1) существование
предела функции К(h) эквивалентно существованию производной
(конечной или бесконечной), причем
![]() = Ко
= f/ (xо).
= Ко
= f/ (xо).
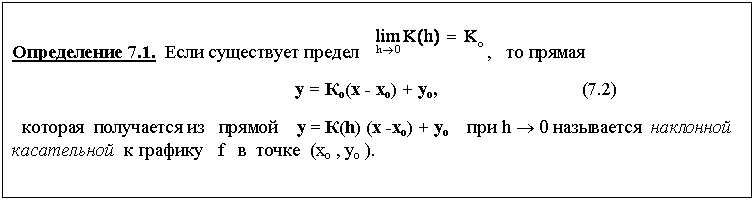
Предельное положение секущей Мо Мh при h ® 0 называется касательной к графику f в точке хо.
В результате мы пришли к следующей теореме.
Теорема 7.1. Пусть функция f непрерывная при х = хо. В точке (хо, f (хо)) существует наклонная, касательная к графику функции f, тогда и только тогда, когда f имеет в точке хо производную. При этом уравнение касательной имеет вид у = f/(xо) (x -xо) + yо и, значит, производная в точке хо равна тангенсу угла наклона касательной к оси ОХ, а дифференциал в точке хо равен приращению ординаты касательной.
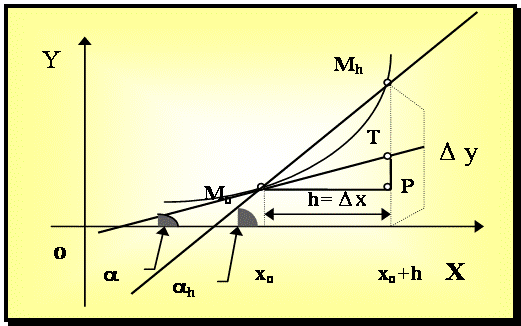
Рис.7.2.
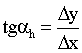 , тогда получим
, тогда получим 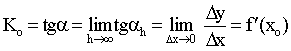
PT = Dx × tg a = h × tg a = y/ × dx = dy.
Таким образом, дифференциал функции у = f(х)
в точке хо равен приращению
ординаты касательной к графику функции в этой точке, когда хо получает приращение D х .
Заметим, что Dу ¹ dy
То есть отсюда мы имеем приближенное равенство:
f(xo + Dx) - f(xo) @ f/(xo) × Dx (7.4)
f(xo + Dx) @ f(xo) + f/(xo) × Dx (7.5)
Таким образом, наклонная касательная к графику функции обладает тем свойством, что разность ординат графика функции и этой касательной есть величина бесконечно малая по сравнению с приращением аргумента при х ® хо.
8. Основные правила для дифференцируемых функций

Д о к а з а т е л ь с т в о. (Самостоятельно).
Следствие 1. Пусть выполнены условия теоремы для u = f(x),
с - const, тогда (c × u)/ = c × u/ .
Следствие 2. Пусть выполняется условие теоремы для последовательности
функций u1 = f1 (x), u2 = f2 (x), . . . , un = fn(x)
и c1, c2, . . . , cn - const.
Тогда
(c1 × u1 + . . . + cn un)/ = c1 u1/ + . . . + cn × un/ .
Свойства функции 1, 2, 3 переносятся на дифференциалы функции при тех же предположениях в точке хо.
1. d (u1 + v2)
= du1 + dv2 ,
d (cu) = c × du;
2. d (u1 × v2) = v2 du1
+ u1dv2 ;
3. d 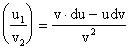
8.1.
Производная обратной функции

Д о к а з а т е л ь с т в о: Зафиксирована окрестность О(хо), в которой выполнены условия теоремы, тогда обратная функция определена, однозначна и непрерывна на некотором интервале, содержащем точку уо, а именно на образе указанной выше окрестности точки хо и, значит, если Dх =х - хо, Dу = у - уо, у = f(х) то условия Dх ® 0 и Dу ® 0 эквивалентны.
![]()
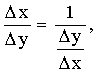 при Dх ® 0
при Dх ® 0
существует предел левой части, т.к. существует предел правой части
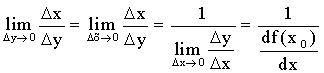
Но  поэтому
поэтому 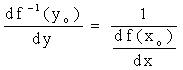 , что и требовалось
доказать.
, что и требовалось
доказать.
Геометрическая интерпретация доказательства очевидна.
|
|
Из геометрического смысла производной
имеем ![]() ,
, ![]() .
.
Очевидно,
что ![]() , поэтому
, поэтому
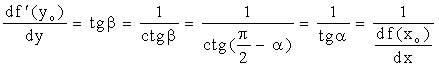 .
.
Примеры:
1. y = arcsin x, x = sin y
![]()
![]()
![]()
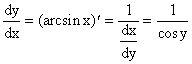
так как ![]() , то cos y ³ 0, поэтому
, то cos y ³ 0, поэтому
![]() .
.
2. ![]() , - самостоятельно.
, - самостоятельно.
3. ![]() , - самостоятельно.
, - самостоятельно.
4. ![]() , - самостоятельно.
, - самостоятельно.
5. y = loga x, x = ay, a > 0, a ¹ 1, x > 0 , y Î (-¥; +¥)
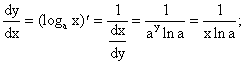
если ![]() .
.
8.2.
Производная и
дифференциал сложной функции

Д о к а з а т е л ь с т в о: так как y = f(x), z = F(y) имеют производную в точке хо, то они непрерывны (см. теорему 5.1) соответственно в точке хо, уо и имеем сложную функцию Ф(х) = F[f(x)], которая дифференцируема в точке уо
D z = F¢(yo) Dy + e(Dy) × Dy, (8.3)
где ![]() функция не
определена при Dу = 0, но мы доопределим:
при Dу = 0 положим e(o)=0, тогда e (Dу) будет непрерывна и при Dу = 0.
функция не
определена при Dу = 0, но мы доопределим:
при Dу = 0 положим e(o)=0, тогда e (Dу) будет непрерывна и при Dу = 0.
Поделим обе части уравнения (8.3) на Dх ¹ 0.
Получим
![]() (8.4)
(8.4)
у = f(x) имеет производную в точке хо , т.е. существует ![]() ,
,
а
из существующей производной f¢(хо ) следует непрерывность функции у = f (х)
в точке хо: ![]()
При Dх = 0 имеет Dу = 0,
следовательно, Dу как функция от Dх, непрерывна в
точке Dх = 0. Поэтому согласно
правила замены переменных в пределах непрерывных функций имеем ![]()
Теперь в (8.4), переходя к пределу при Dх ® 0, получим (8.3).
Следствие 1. Инвариантность формы первого дифференциала относительно выбора переменных
dz = F¢ (yo ) dy = Ф¢ (хo ) dx (8.5)
Следствие 2. Эту теорему по индукции можно распространить на любое конечное число суперпозиций функции.
Пример: z (y (x (t))) в случае дифференцирования z (y), y (x), x (t) в соответствующих точках имеет место формула
![]()
В случае сложной функции для обозначения производной используется нижний индекс, указывающий, по какой из переменных берется производная
![]()
Примеры:
1. Пусть у = хa, х > 0
нужно
определить ![]() .
.
Пусть хa = lu, где u = a × ln x, тогда
![]()
(xa )¢ = a × xa-1.
2. ![]()
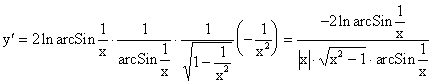
3. Пусть F (x, y) = 0, т.е. функция задана неявно, нужно найти производную такой функции.
F(x, y(x)) º
0 рассмотрим как сложную функцию и
определим ![]() .
.
x2 + y2 = 25
![]()
Метод дифференцирования неявных функций может быть применен к выводу формул, полученных ранее.
Пусть U = u(x) - дифференцируемая функция, то
(Sin U)/ = U/ × cos u; (lu )/ = lu × u/;
(Cos U)/ =
-U/ sin u; ![]()
![]()
![]()
![]()
![]()
Если u = x тогда, получим производные основных элементарных функций.
9.
Понятие о
производных и дифференциалах высших порядков
Производная f¢(x) от функции F(x) называется производной первого порядка и представляет собой некоторую функцию. И, если эта функция тоже имеет производную, тогда производная от производной первого порядка называется производной второго порядка и обозначается f¢¢(x), т.е. f¢¢ (x) = [f¢ (x)]¢.
Аналогично определяется производная f(n) (x) любого порядка
n=1, 2, ... ; если существует производная f(n-1) (x) n-1 порядка ( при этом под производной нулевого порядка подразумевается сама функция f(o) (х) = у = f(x).
Согласно определения производной в точке хо получим
![]()
З а м е ч а н и е. Когда говорят, что f имеет в точке хо производную порядка n, то это значит, что в некоторой окрестности точки хо у функции f существуют все производные низших порядков.
Пусть х - независимая переменная и у = f (x) есть дифференцируемая функция на некотором интервале (а, в). Тогда
df (x) = f¢ (x) dx; есть функция двух переменных: x и dx.
Будем предполагать, что dx - дифференциал независимой переменной х - имеет произвольное, но фиксированное значение.
Если существует вторая производная f¢¢(x), то df(x) имеет дифференциал и он называется вторым дифференциалом.
![Подпись: Определение 9.1. Дифференциалом второго порядка (или вторым дифференциалом) d2 f(x) функции f(x) называется дифференциал от дифференциала первого порядка этой функции
d2 f(x) = d [df (x)]. (9.6)](06.files/image102.gif)
Аналогично, дифференциалтретьего порядка d3f(x) = d [d2 f (x)].
Так последовательно определяются дифференциалы высших порядков.
Выведем формулу для дифференциала второго порядка. Пусть f(x) - дважды дифференцируема (т.е. имеет вторую производную), т.к.
df(x) =f¢ (x) dx, тогда согласно (9.6) имеем d2 f(x) = d [df (x)].
Если х - независимая переменная, то dx, равный Dх, очевидно, не зависит от х по отношению к переменной х играет роль постоянной.
d2 f(x) = d [f¢ (x) dx] = dx × d [f¢ (x)] = {f¢ (x) - снова некоторая функция от х} = [ f¢¢ (x) dx] dx = f² (x) dx2, где dx2 = (dx)2.
Таким образом, мы доказали теорему.

З а м е ч а н и е. Формула d2 f(x) = f² (x) dx2, вообще говоря неверна,если х не является независимой переменной, т.к. dx нельзя рассматривать как множитель, не зависимый от х.
10. Приложения производной
10.1. Теоремы о среднем для дифференцируемых
функций

Д о к а з а т е л ь с т в о:
Пусть для определенности f в точке x принимает наибольшее значение, т.е. f(x)£f(x) для всех xÎ (a,b), тогда, если x<x
![]() ,
(10.1)
,
(10.1)
если x<x
![]() .
(10.2)
.
(10.2)
Если
существует производная  , то в пределе при х® x-0 из (10.1) получим, что
f/(x)³0,
а из (10.2) при х®
x+0
Þ
f/(x)£0,
что возможно лишь в случае f/(x)=0.
, то в пределе при х® x-0 из (10.1) получим, что
f/(x)³0,
а из (10.2) при х®
x+0
Þ
f/(x)£0,
что возможно лишь в случае f/(x)=0.
|
|
Геометрическая интерпретация теоремы Ферма состоит в том, что если в точке xÎ (a,b) функция f принимает наибольшее или наименьшее значение, то касательная в точке (x,f(x)) к графику функции параллельна оси Ох.
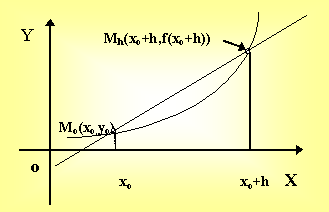

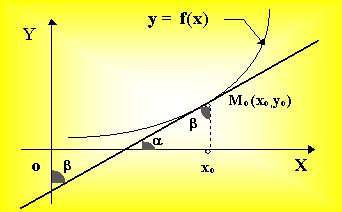 Рис. 8.1.
Рис. 8.1.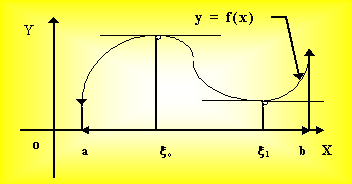 Рис. 10.1.
Рис. 10.1.