Теорема 10.2. (Ролль). Пусть функция f:

                                      1. непрерывна на отрезке [a,b];

                                      2. имеет в каждой точке интервала (a,b)  производную;

                                      3. f(a) = f(b).

                                      Тогда существует точка x такая, что  f/(x) = 0,  a < x < b.

 

Д о к а з а т е л ь с т в о:

         Пусть f  непрерывная на [a,b] принимает на этом отрезке наибольшее и наименьшее значения в некоторых точках этого отрезка. Обозначим

М = max f(x), m = min f(x)  тогда для всех  x Î [a,b] справедливо m £  f(x) £ M.

         Если m = M Þ f - const и, следовательно, f/ º 0.

         Если m ¹ M Þ из условия f(a) = f(b) следует, что хоть одно из значений m или M не принимается на концах [a,b]. Пусть, например, это будет точка М, т.е.  существует xÎ (a,b), что f(x) = М. Тогда из теоремы 10.1 следует, что f/ = 0.

 

        

 

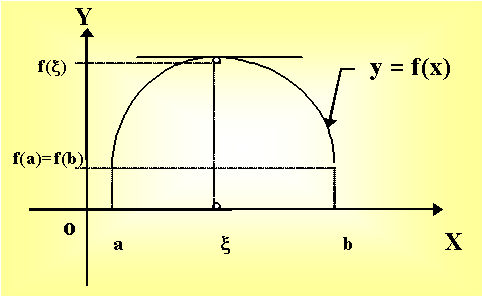
Геометрически теорема Ролля означает, что если выполнены условия теоремы, то существует точка, в которой касательная параллельна оси абсцисс.

 

 

 

 

 

 

 

 

 

                                                                 

Рис. 10.2.

 

         Другая формулировка теоремы Ролля.

Между двумя последовательными корнями дифференцируемой функции всегда содержится по крайней мере один корень ее производной.

 

З а м е ч а н и е. Все три условия теоремы существенны.

Если не выполняется одно из условий, то не существует такой точки

 xÎ (a,b), что f/(x) = 0.

Рис.10.3.

 

Примеры:

1. f(х) определена на [0,1] и равна х.

 

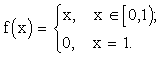
f удовлетворяет условиям 2 и 3, но не удовлетворяет условию 1.

 

 

Рис.10.4.

 

 

 

2. f(x) = çx ç, x Π [-1,1]

f удовлетворяет условиям 1 и 3, но не удовлетворяет условию 2.

 

 

 

 

 

Рис. 10.5.

 

 

 

3. y = x,    x Π [0,1]

f удовлетворяет условиям 1 и 2, но не удовлетворяет условию 3.

 

 

 

 

 

         Обобщением теоремы Ролля является следующая теорема.

 

Теорема 10.3. (Лагранж). Пусть f  непрерывна на [a,b]  и имеет производную в каждой точке интервала (a,b). Тогда существует такая точка x ,что:

         f(b) - f(a) =  f/(x)(b-a) , a<x<b                                                          (10.3)

 

Д о к а з а т е л ь с т в о:

         Рассмотрим вспомогательную функцию

                            F(x) = f(x) - lx,                                                                   (10.4)

где число l выберем таким образом, чтобы F(a) = F(b), т.е. чтобы

f(a) - la =  f(b) - lb. Для этого достаточно взять

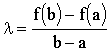                                                                                                 (10.5)

Тогда для F(x) выполнены условия теоремы Ролля: F(x) - непрерывна на [a,b], дифференцируема на (a,b) и принимает на концах одинаковые значения, поэтому существует такая точка  x Î (a,b), что F/(x) = 0. Тогда из (10.4) получаем F/(х) =  f/(х)-l, поэтому  f/(x) - l=0 и из (10.5) получим

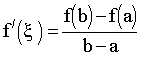                                                                                          (10.6)

 

Рис. 10.6.

        

 

 

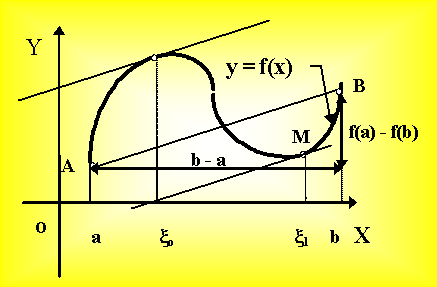
Геометрический смысл теоремы Лагранжа состоит в следующем.

Пусть А(а,f(а)), В(b,f(b)) - точки графика функции f, АВ - хорда, соединяющая точки А и В. Тогда отношение .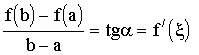

Т.е. в условиях теоремы можно сказать, что найдется точка, возможно не одна, в которой касательная к графику параллельна хорде .

 

 

 

 

 

 

 

З а м е ч а н и е. Теорема Лагранжа найдет ряд важнейших приложений в дальнейшем.

         Запишем другую форму (10.6)  

                                               f(a) - f(b) = f/(x) (a-b)                                     (10.7)

т.е. она справедлива для a>b и b>a.

 

Следствие 1. Если f/(х) = 0  " х Î (a,b)  Þ  f(х) = С - const.

 

Д о к а з а т е л ь с т в о:

         Пусть f/(х) = 0 при х Î (a,b) тогда для любого х Î (a,b)

  f(х) - f(b) = 0×(х-b). Следовательно   f(х) = f(b)= const.

 

Следствие 2. Если f(х), g(x) - дифференцируемые на (a,b) и     (в этих точках)

 f/(х) = g/(x) " х Î (a,b) , а на концах промежутка, если они входят в область определения, - непрерывны, то эти функции отличаются на С - Сonst:

 f(х) - g(x) = С.

 

Д о к а з а т е л ь с т в о: Пусть f/(х) = g/(x) при х Î <a,b>, тогда на этом промежутке  êf(х) - g(x)ê/ =  f/(х) - g/(x) = 0. В силу следствия 1 имеем

         F/(х) = 0   Þ   F(x) = С,  а здесь F(х) =  f(х) - g(x) = С.

 

10.2. Возрастание и убывание функции одной переменной

 

Определение 10.1.   Функция f(х) возрастает на промежутке <a,b>, если из того, что х2 > x1  Þ  f(х2) >  f(х1)  "  x1,x2 Î <a,b>. И  f(х) убывает на промежутке <a,b>, если х2 > x1 Þ  f(х2) < f(х1)  "  x1,x2 Î <a,b>.

 

Теорема 10.4. (необходимый признак возрастания (убывания) функции).

                   1. Если f(х) возрастает и дифференцируема на <a,b>  Þ f/(х) ³0                          "  x Î <a,b>.

                   2. Если  f(х) убывает и дифференцируема на <a,b>   Þ   f/ (х) £0                          для всех  x Î <a,b>.

 

Д о к а з а т е л ь с т в о:

 

         1).Пусть f(х) - дифференцируема и возрастает на  <a,b>. Согласно определению производной,

.

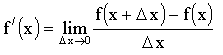Если х, х+Dх Î <a,b>, то в силу возрастания знак приращения функции f(x+Dх)- f(x) совпадает со знаком приращения Dх (где Dх¹0). Следовательно,

                                                         .                                     (*)

Переходя в (*) к пределу при Dх ® 0, имеем f/(x)³0.

 

         2). Доказательство второй части теоремы аналогично.

 

         Если f убывает, то согласно определению, х2 > x1  Þ  Dх > 0 и 

f(x+Dх) - f(x) £0  следовательно f/(x) £ 0 (рис.10.7. b)).

 

 

 

Рис.10.7.

 

 

Теорема 10.5. (достаточный признак возрастания и убывания функции).

1. Если f/(x) > 0, "  x Î <a,b>,  тогда  f(x) возрастает на этом промежутке.

2. Если f/(x) < 0, "  x Î <a,b>,  тогда f(x) убывает на этом промежутке.

 

Д о к а з а т е л ь с т в о:

Пусть f(x) такая, что f/(x)>0 при a<x<b. В силу теоремы Лагранжа  "  x1,x2 Î <a,b> можно записать f(x2) - f(x1) =  f/(x)( x2- x1),  где x Î ( x1, x2), т.е. a£ x1< x2£b. Но так как f/(x) > 0 и x2 - x1 > 0 Þ f(x2) - f(x1) > 0 или f(x2) > f(x1). По определению, f(x) - возрастает.

2. Доказать самостоятельно.

 

З а м е ч а н и е. Если функция f(x) возрастает или f(x)  убывает, то она называется монотонной. Промежутки возрастания или убывания функции называются промежутками монотонности.

 

10.3. Понятие о правиле Лопиталя

 

         При определении предела некоторой функции, заданной аналитически, при  х ® a или ¥, +  ¥, -  ¥, при формальной подстановке этой величины в качестве аргумента в формулу получаем неопределенности вида:    или 1¥.

         В этом случае нельзя судить о существовании предела. Наряду с основными методоми раскрытия неопределенности при нахождении предела существуют и другие, которые носят название правил Лопиталя.

         Рассмотрим отношение   ,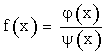

где j(х), y(х) определены и дифференцируемы в некоторой окрестности О(а) точки а, исключая, быть может, саму точку а. Может случится, что при

 х ® а    j(х), y(х) ® 0 или ¥ или одновременно являются бесконечно малыми или бесконечно большими. Тогда говорят, что в точке а имеет место неопределенность вида  . В этом случае, используя производные  j/(х), y/(х) можно сформулировать простое правило для нахождения предела f(x) при х ® а.

 

Теорема 10.6. (Лопиталь). Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношений их производных (конечному или бесконечному), если последний существует в указанном смысле.

 

Д о к а з а т е л ь с т в о:

         Пусть 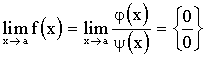 для простоты еще предположим, что j(х), y(х), j/(х), y/(х) непрерывны в точке а и y/(a)¹0.

Итак, пусть                         (1)

                                            (2)

Разность j(х)- j(а) можно рассматривать как приращение функции j(х) в точке а, соответствующее приращению Dх = х - а. Поэтому

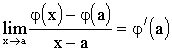                       ,                 (3)

Аналогично,

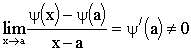                                     (4)

Учитывая (1), (2), при х¹а получим 

,

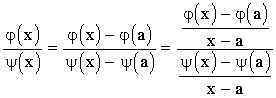переходя к пределу при х ® а будем иметь

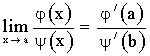                    .                        (5)

 

Но мы предположили, что  j/(х), y/(х) непрерывны при х ® а, причем y/(a)¹0, поэтому

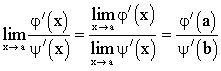                   .           (6)

Сопоставив (5) и (6), получим правило Лопиталя

.

 

Примеры:

                   1) ;

                   2).

З а м е ч а н и е. Неопределенность вида 0×¥, ¥ - ¥  нужно привести к виду   или  и применить правило Лопиталя.

                   3)

Функции вида    сначала надо прологарифмировать, а затем применять правило Лопиталя.

 

Пример.

,

 

 .

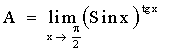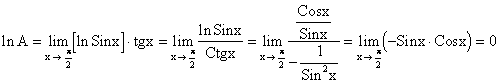Окончательно А = ео = 1.

 

11. Формула Тейлора

 

11.1. Вывод формулы Тейлора для многочлена

 

         Пусть данный многочлен

                                      Р(х) = а0 + а1×х + а2 ×х2 + ... + аn×хn                          (11.1)

требуется разложить по степеням бинома х - х0 , где х0 - некоторое число.

Представим

                   Р(х) = A0+A1× (х - х0 ) + A2× (х - х0 )2 + ... + An×(x-х0)n                     (11.2)

т.е.  пусть это наше искомое разложение и теперь определим коэффициент Аi (i=0¸n). Для этого применим так называемый метод неопределенных коэффициентов.

         Полагая х = х0 в тождестве (11.2), получим Р(х0) = А0.

         Дифференцируя (11.2), будем иметь

                            Р/(х) = A1 + 2×A2× (х - х0 )2 + ... + n×An×(x-х0)n-1     

Положим х = х0 . Получим , что Р/(х0) = А1.

         После вторичного дифференцирования находим

                            Р//(х) = 2!×A2× (х - х0 ) + ... + n×(n-1)×An×(x-х0)n-1.

Откуда        . 

 

         Очевидно, что, используя этот прием, получим общую формулу:

                                    ,                                        (11.3)

где по определению полагают P(0)(x)= P(x) и 0!=1.

         Эту формулу можно доказать методом математической индукции (самостоятельно).

Подставим теперь коэффициенты (11.3) в (11.2). Получим формулу Тейлора для многочлена

                               .             (11.4)

Или короче

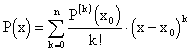                                .                                                 (11.5)

З а м е ч  а н и е. Нетрудно убедиться, что старшие коэффициенты в (11.1) и (11.2) совпадают. Поэтому справедливо равенство

         Если положить х=0, то правая часть равенства (11.5) равна правой части (11.1), поэтому справедливы равенства

.

 

11.2. Бином Ньютона

 

         Рассмотрим функцию      f(x) = (a+x)n,    n - натуральное               (11.6)

Полагая х0 = 0 и используя формулу Тейлора, получим 

(a+x)n=A0+A1×x+ ... +An×xn,        где

.

         Так как  из (11.6) получаем

,

то f(0)=an  и 

Таким образом, А0 = аn и

Аk будем называть биномиальным коэффициентом и обозначать

                                                                                                             (11.7)

Запишем теперь биномиальную формулу Ньютона

.

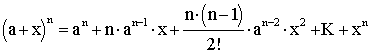         В частности, при а = 1

.

11.3. Формула Тейлора для функции

 

         Пусть y=f(x) имеет непрерывную производную N-го порядка (fN(х)) (т.е. $ непрерывные производные на (a,b) f(x) = f(0)(x), f(1)(x),¼) в интервале (a,b) и х Î (a,b). Воспользуемся многочленом Тейлора (11.5) степени n, n £ N

.

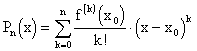         Многочлен Рn(х) можно рассматривать как некоторое приближение (аппроксимацию) данной функции. Обозначим через Rn(х) соответствующую ошибку (так называемый остаточный член), тогда будем иметь f(x) =  Рn(х) + Rn(х).

         Покажем, что при х ® х0 остаточный член Rn(х) будет бесконечно малой порядка выше n.

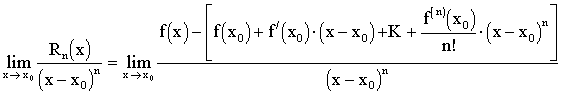
Очевидно, что имеем неопределенность вида . Применяя правило Лопиталя последовательно n раз и учитывая непрерывность производной f(n)(x), находим

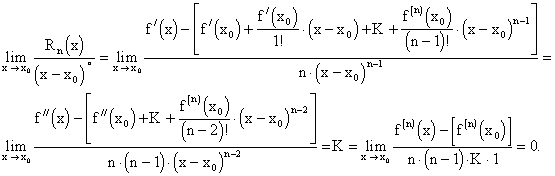
Следовательно, Rn(х)=о[(х-х0)n].

         Таким образом, мы получим локальную формулу Тейлора:

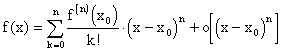                         .                                     (11.8)

З а м е ч а н и е. В частности, в случае a<x<b, x=0 будем иметь формулу Маклорена:

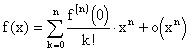                            .                                                    (11.9)

 

Пример: Пусть f(x) = Sin x; аппроксимировать в окрестности точки х=0 многочленом Тейлора Р(х). Имеем

         f(x) = Sin x,  f/(x) = Cos x,  f//(x) = -Sin x,  f///(x) = -Cos x.

Отсюда f(0)=0, f/(0)=1, f//(0)=0, f///(0)=-1. На основании формулы (11.9) имеем

.

11.4. Экстремум функции одной переменной

 

Определение 11.1. Будем говорить, что f(x) имеет максимум в некоторой точке х=х1, если в некоторой окрестности О(х1) (возможно, весьма малой) выполнено неравенство  f(x1) > f(x) , (x¹x1).

         Аналогично определим минимум функции f(x). Если при х=х2

Рис. 11.1.

f(x2) < f(x)  (х¹х2) в некоторой окрестности точки О(х2), то в точке х2 f(x) имеет минимум.

 

Максимум или минимум функции называется экстремумом функции. Те точки, где f(x) достигает своих экстремальных значений, назовем точками экстремума функции.

 

 

 

Рис. 11.2.

         Из определения следует, что экстремум функции носит локальный характер. То есть может оказаться, что минимум функции принимает большее значение, чем максимум.

         Здесь речь идет о двустороннем экстремуме (в дальнейшем мы под словом экстремум будем всегда понимать двусторонний экстремум). Ниже мы введем понятие односторон-него (краевого)  экстремума.

 

Теорема 11.1. (Необходимое условие экстремума функции).

В точке экстремума (двустороннего) дифференцируемой функции производная ее равна нулю.

(Это есть теорема Ферма, которая  доказана ранее)

 

С л е д с т в и е. Непрерывная функция может иметь экстремум лишь в тех точках, где производная равна нулю или не существует.

 

          Рассмотрим теперь достаточные условия экстремума. Из того, что f/(x0) = 0, вовсе не следует, что f(x) имеет экстремум при х =  х0.

Пример. Пусть y = x3 . При  х0 = 0  f/(x) = 3×х2 êх=0 = 0, но f(0) не является экстремальным значением.

 Определим  достаточное условие экстремума.

Теорема 11.2. (Первое правило). Если f(x)  дифференцируема и для некоторого х = х0  f/(x0) = 0, а также f/(x)  меняет свой знак при переходе через это значение, то число f(x0) является экстремумом функции f(x), причем:

1. f(x) имеет max  при х=х0  , если f/(x) меняет знак с “+” на “-”.

2. f(x) имеет min  при х=х0  , если f/(x) меняет знак с “-” на “+”.

 

Д о к а з а т е л ь с т в о.

         1). Пусть f(x) = 0, причем f/(x) >  0 при х0 - e  < х < х0 и f/(x) < 0 при

 х0 < х < х0+e, где e - достаточно малое положительное. Но если f/(x)>0 Þ f(x) возрастает, т.е.

 " хÎ (х0-e, х0)  f(x0) > f(x), а для  " хÎ (х0, х0+e)  f(x0)< f(x), но тогда в точке x0  f(x) имеет максимум.

2). Самостоятельно.

 

Теорема 11.2/. Если производная дифференцируемой функции f(x) в некоторой точке х=х0 обращается в нуль, но при переходе не меняет свой знак, то f(x) в данной точке не имеет экстремума.

Д о к а з а т е л ь с т в о. Самостоятельно.

 

Теорема 11.3. (Второе правило). Если дифференцируемая функция в некоторой точке х0 имеет первую производную, равную нулю, а вторая производная существует и отлична от нуля (f/(x0)=0, f//(x0)¹0), то в этой точке функция f(x) имеет экстремум, а именно

         1. если f//(x0) > 0, тогда f(x0) - min,

         2. если f//(x0) < 0, тогда f(x0) - max.

 

 Д о к а з а т е л ь с т в о.

 

         1). Пусть f/(x0)=0, f//(x0) > 0 и х=х0+Dх0 - точка, близкая к х0.

, (так как f/(x0)=0). Таким образом, величина  стремится к пределу f//(x0)¹0, а значит, начиная с некоторого момента , эта величина имеет знак своего предела (см. теорему 5.2, следствие). У нас “+”. Поэтому  при 0 < êx-x0 ê< e  " e > 0. Отсюда получаем, что числитель и знаменатель имеют один знак, и, следовательно,

          f/(x) > 0 при х0 < х < х0+e,

          f/(x) < 0 при х0-e < х < х0, а при переходе через точку х0  f/(x) меняет знак с “-” на “+”. На основании теоремы 11.2  f(x0) - минимум функции f(x).

 

         2). Доказать самостоятельно.

 

Пример из микроэкономики.

Назад  Далее