12. Исследование поведения функции

12.1. Выпуклость и вогнутость графика функции. Точки перегиба

Определение 12.1. График дифференцируемой функции y = f (x)

называется вогнутым вверх (или выпуклым вниз) в промежутке < а, в > , если соответствующая часть кривой y = f (x) (x Î < a, b >) расположена выше касательной, проведенной в любой ее точке M (x, f(x)).

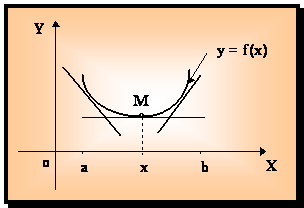
Рис. 12.1.

Определение 12.1^/ y = f (x) (x Î < a, b >) называется выпуклым вверх (или вогнутым вниз) в промежутке < а, b >, если соответствующая часть кривой y = f (x) расположена ниже касательной, проведенной в любой точке M (x, f (x)).

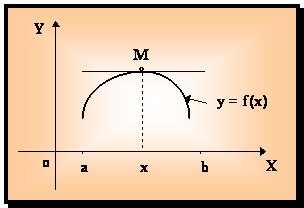
Рис. 12.2.

Теорема 12.1. (Достаточные условия выпуклости графика)

1. Если для дважды дифференцируемой функции y = f (x) вторая производная f^² (x) > 0 " x Î < a, b> , то график этой функции выпуклый вниз в данном промежутке.

2. Если f^² (x) < 0 (x Î < a, b >), то график у = f (x) выпуклый вверх.

Д о к а з а т е л ь с т в о: Пусть f^² (x) > 0 при а < х < в и х_о Î< а, в >. Сравним ординату в точке х функции у = f (x) с ординатой ее касательной в точке х_о

. (12.1)

Рассмотрим (12.2)

Используя теорему Лагранжа, будем иметь

f (x) - f (x_o) = f^/ (x ) (x - x_o), где x Î (x_o, x),

тогда получаем

d = (x -x_o ) [f^/ ( x ) - f^/ (x_o) ] (12.3)

Далее, f^²(x) = [f^/ (x)]^/ > 0 Þ f^/ (x) возрастает.

Пусть х < х_о , тогда x < x_o и, следовательно, в силу возрастания f^/ (x) имеем f^/ (x) < f^/ (x_o) из (12.3) имеем, что d > 0.

Рис. 12.4.

Если теперь x > x_o Þ x > x_o, поэтому f^/ (x) > f^/ (x_o), но d > 0 снова.

То есть при x ¹ x_o, имеем , то есть так как x_о - произвольная точка, то при " х Î < а.в > кривая y = f (x) расположена выше своих касательных и, значит, график y = f (x) выпуклый вниз.

(2. Доказать самостоятельно )

Определение 12.2. Точкой перегиба графика дифференцируемой функции

y = f (x) называется его точка, при переходе через которую кривая меняет свою вогнутость на выпуклость или наоборот.

Теорема 12.2. Если для функции y = f (x) в некоторой точке x_о f^² (x_o ) = 0 и при переходе через эту точку меняет свой знак на обратный, то точка М(х_o,f(x_o)) является точкой перегиба функции.

Д о к а з а т е л ь с т в о: Пусть f^² (x_o ) = 0 в точке М (х_о , f (x_o)) меняет свой знак, для определенности, с “+” на “ -”. Тогда левее точки х_о

(х < х_о) f^² (x) > 0, а поэтому при х_о - e < х < х_о график этой функции выпуклый вниз.

Для х > х_о, т.е. при х_о < х < х_о + e у = f (x) выпукла вверх (Ç).

Таким образом, в точке М кривая y = f (x) меняет вогнутость; согласно определения М - точка перегиба.

З а м е ч а н и е. В точке перегиба х_о функции y = f (x) f^² (x) может также не существовать; например, обращаться в бесконечность.

Пример. (Кривая Гаусса).

.

Рис. 12.5.

Тогда и , решая уравнение

получим .

Таблица 12.1.

x	(-¥; - )	-	(- ; )		(; +¥)
y^//	+	0	-	0	+

Следовательно, точки точки перегиба

12.2. Асимптоты

Определение 12.3. Пусть y = f (x) определена для всех х > а (соответственно, х < а). Если существуют такие к, l : f(x) - kx - l = 0 (1) при х ® + ¥ (соответственно, х ® -¥), то прямая

у = к х + l

называется асимптотой функции при х ® +¥ (соответственно, х ® -¥).

Рассмотрим геометрический смысл асимптоты.

Рис. 12.6.

Пусть точка М(x,f(x)) точка графика функции f. Тогда расстояние МР ® 0 при х ® ¥, но в этом случае и MQ ® 0 т.е. эти два условия эквивалентны.

Рассмотрим способ отыскания асимптоты, т.е. метод определения коэффициентов к, l.

Пусть х ® +¥ (аналогично х ® -¥) и пусть y = f (x) имеет асимптоту у = кх + е. Тогда по определению 12.3.

f (x) = kx + l + 0 (1) . (12.4)

Разделим обе части уравнения на х и перейдем к пределу при х ® +¥. . (12.5)

Определив k по формуле (12.5) из (12.4), теперь можно определить

(12.6)

Т.е. отыскание уравнения касательной сводится к отысканию пределов (12.5) и (12.6). Более того, мы показали, что если существует представление функции f в виде (12.4), то к и l определяются по (12.5) и (12.6). Таким образом, представление (12.4) единственно.

Определение 12.4. Пусть f определена в некоторой окрестности точки х_о (быть может односторонней) и пусть , или

или то и другое. Тогда прямая х = х_о называется вертикальной асимптотой.

Рис. 12.7.

Пример: .

Так как , то прямая x = - 1 вертикальная асимптота.

12.3. Построение графиков

Изучение заданной функции и построение ее графика с помощью развитого нами аппарата можно проводить, например, в следующем порядке.

1. Определить область существования функции, область непрерывности, точки разрыва. Полезно также выяснить симметрию графика ( четность, нечетность, периодичность и т.п.). Исследовать поведение функции в точках разрыва х ® а, х ® b, где а и b граничные

точки области существования. Решить уравнение f (x) = 0, найти точки пересечения с осями координат(y = f (0) ).

2. Найти асимптоты.

3. Приблизительно, вчерне, нарисовать график функции.

4. Вычислить f^¢ (x), если нужно f^² (x), решая последовательно уравнения f^¢ (x) = 0 и f^² (x) = 0. Находим критические значения аргумента для функции. Изучая затем значение f^¢ (x) в каждом из промежутков между критическими значениями, определяем промежутки возрастания, убывания и выясняем характер этих критических значений.

5. Решая f^² (x) = 0 и рассматривая поведение f(x) на промежутках существования, определить выпуклость ( È , Ç ) графика функции, максимумы, точки перегиба, если они есть в наличии.

6. Составить таблицу значений функции ее характеристических точек (граничные точки области существования, точки разрыва, точки пересечения с осями координат, точки экстремума, точки перегиба и т.д.).

7. Окончательно вычертить график.

Пример. Построить график функции

.

Эта функция определена и непрерывна для всех х ¹ -1. Она имеет асимптоты у = х - 4 и х = -1, причем , .

Представим функцию , тогда очевидно, что f(x) > x - 4 при х > -1 (график находится над асимтотой) и при x < -1; f(x) < x - 4 (график находится под асимтотой).

График функции f(x) пересекает ось Ох в точках, в которых х²-3х-2 = 0, т.е. при . Ось Оу график пересекает в точке у = -2.

Определим теперь точки экстремума, перегиба и интервалы выпуклости функции вверх или вниз. Для этого найдем у^/ и у^// :

, .

Отсюда видно, что у^/ = 0 в точках х = -1- @ -2,4 и х = -1+ @ 0,4. В точке х = -1 производные не существуют.

Выполнив последовательно все пункты, указанные выше, занесем их в таблицу.

Таблица 12.2.

х	(-¥; -1-)	-1-	(-1-;-1)	-1	(-1;-1+)	-1+	(-1+; +¥)
у^/	+	0	-	нет	-	0	+
у^//	-	-	-	нет	+	+	+

Найден общий характер поведения функции, а это позволяет нарисовать график.

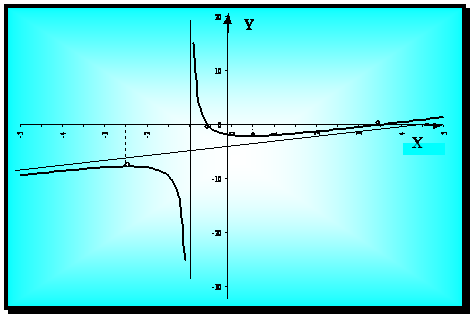
Рис. 12.8.

13. Дифференциальное исчисление функции многих переменных

13.1. Частные производные первого порядка

Пусть задана функция Z = f(x,y). Для простоты будем предполагать существование функции в некоторой окрестности рассматриваемой точки M(х,у).

Рассмотрим отношение частного приращения D_xZ = f(x+Dx,y)-f(x,y) по переменной х к приращению Dх, т.е.

(13.1)

Теперь устремим Dх ® 0. Если предел в (13.1) существует, то назовем его частной производной (первого порядка) функции Z = f(x,y) по х и будем обозначать

,

т.е.

.

Аналогично

.

Определение 13.1. Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при условии, что последнее стремится к нулю.

Заметим, что если от функции Z = f(x,y) берется производная , то у считается постоянным; если же находится , то х - постоянной. Поэтому частная производная функции нескольких переменных равна производной той функции одной переменной, которая получится, если все независимые переменные данной функции, кроме соответствующей одной, считать постоянными, т.е.

, где у - const и т. д.

Пример 13.1. Пусть Z(х,у) = x³ ×Siny+y⁴.

, .

Пример 13.2. Пусть U = f(x,y,z) = x⁵+4×y³+2×z⁴.

Тогда ; ; .

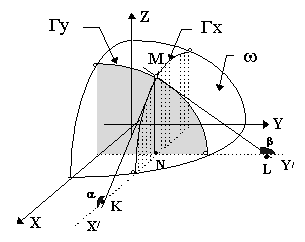
13.2. Геометрический смысл частных производных

Пусть Z = f(x,y); ; .

Изобразим Z = f(x,y) - получим некоторую поверхность.

Рис. 13.1.

Возьмем точки М(х,у,z), N(x,y,0) - проекция точки М на плоскость ХоУ. Полагая у - const, мы получаем плоскую кривую Г_x , представляющую собой сечение поверхности w соответствующей плоскостью, параллельной Оxz. Пусть МК - касательная к кривой Г_x в точке М(х,у,z) и a - угол, образованный с положительным направлением оси Ох. Так как

,

на основании смысла обычной производной имеем , аналогично .

13.3. Полный дифференциал функции

Пусть Z = f(x,y) - функция двух независимых переменных х и у. Полное приращение этой функции

DZ = f(x + Dx, y + Dy) - f(x,y) (13.2)

представляет разность значений данной функции в точках М(х,у) и М^/(х+Dх,у+Dу). Тогда .

Если r ® 0, можно подобрать независящие от Dх и Dу величины А и В такие, что величина (выражения) А×Dх+В×Dу будет отличаться от Dz на величину высшего порядка малости по сравнению с r, и тогда это выражение будет называться главной частью полного приращения функции, т.е.

DZ = А×Dх + В×Dу + g×r , (13.3)

где g ® 0 при r ® 0 (или, то же самое, g ® 0 при Dх ® 0 и Dу ® 0 ).

Выражение (13.3) можно записать и в другом виде.

Рис. 13.2.

Поскольку Dх = r×Cos j,

Dу = r×Sin j ,

r = Dх×Cos j + Dу×Sin j.

Отсюда

DZ= А×Dх+В×Dу+a×Dх+b×Dу, (13.4)

где a = g×Cos j ® 0 и b = g×Sin j ® 0 при r ® 0, т.е. Dх ® 0 и Dу ® 0, и обратно.

Обобщая определение дифференциала функции одной переменной на случай функции двух независимых переменных, приходим к следующим определениям:

Определение 13.2. Под дифференциалом независимой понимается приращение этой переменной, т.е. dx = Dx и dy = Dy.

Определение 13.3. Полным дифференциалом функции Z = f(x,y) двух независимых переменных х и у называется главная линейная часть полного приращения этой функции.

Это определение распространяется на функции любого числа переменных. Обозначая дифференциал

dZ= А×Dх + В×Dу,

где А и В не зависят от Dх и Dу и, более того,

DZ - dZ=a×Dх+b×Dу,

где a, b бесконечно малые при Dх ® 0 и Dу ® 0.

Функция, имеющая дифференциал в данной области, называется дифференцируемой в этой области. Если она дифференцируема, то имеет место (13.3) или (13.4).

Если Z = f(x,y) дифференцируема, она непрерывна. Действительно, переходя к пределу в (13.3), получим , т.е. Z - непрерывна.

Пример 13.3. Пусть Z = x×y. Определить полный дифференциал dZ .

Функцию Z можно рассматривать как площадь прямоугольника.

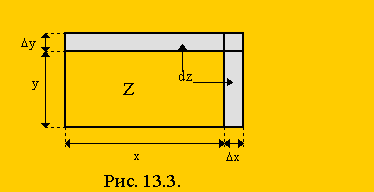
Дадим приращения Dх и Dу. Тогда DZ есть площадь заштрихованной области:

DZ=(х+Dх)×(у+Dу) - х×у=у×Dх+х×Dу+Dх×Dу.

Главная часть этого приращения есть дифференциал

dZ = у×Dх + х×Dу

Теорема 13.1. Дифференциал функции равен сумме произведений частных производных этой функции на дифференциалы соответствующих независимых переменных.

Д о к а з а т е л ь с т в о:

Пусть Z = f(x,y) - дифференцируема, т.е. имеет место

dZ = А×Dх + В×Dу (13.5)

Для определения А и В запишем полное приращение

DZ = А×Dх + В×Dу + a×Dх + b×Dу, (13.6)

где a, b бесконечно малые при Dх ® 0 и Dу ® 0.

Полагая Dу=0 в (13.6), получим частное приращение

D_xZ = A×Dx + a×Dу.

Отсюда .

Тогда

Аналогично, если Dх = 0 Þ .

То есть , . Подставляя А и В в (13.5), получим

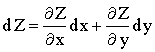(13.7).

С л е д с т в и е. Данная функция имеет единственный дифференциал.

Это следует из теоремы. Если дифференциал функции Z=f(x,y) существует, то он выражается формулой (13.7).

Теорема 13.2. (Достаточное условие дифференцируемости функции).

Если Z = f(x,y) обладает непрерывными частными производными и в данной области, то эта функция дифференцируема в этой области и ее дифференциал выражается формулой (13.7).

(Без доказательства).

Пример 13.4. Пусть дано Z = x^y . Необходимо определить полный дифференциал d Z .

Найдем ; .

Тогда

.

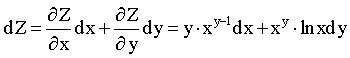З а м е ч а н и е. Если u = f(x,y,z) имеет непрерывные частные производные, то дифференциал этой функции выражается формулой

,

где Dх = dx, Dу = dy, Dz = dz.

Пример 13.5. Найти дифференциал функции .

Находим , , .

Следовательно .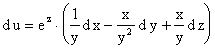

При малых приращениях Dх и Dу приращение дифференцируемой функции Df(x,y) = f(x+Dх,y+Dy) - f(x,y) приближенно можно заменить df(x,y), где df(x,y) = f_x^/(x,y)× Dх + f _y^/((x,y)× Dy . То есть имеем приближенное равенство f(x+Dх,y+Dy) - f(x,y) » f_x^/(x,y)× Dх + f _y^/((x,y)× Dy, которое будет тем относительно точнее, чем меньше çDх ç, çDу ç.

Назад Далее