14. Понятие о производной функции по данному направлению

 

14.1. Производная по  направлению 

 

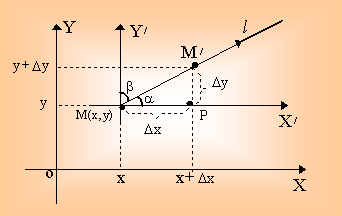
         Пусть u = f(x,y) - функция, определенная в области w. Рассмотрим точку М(х,у) Î w и некоторое направление l, определяемое направляющими косинусами Cosa и Cosb = Sina (т.е. Cosa и Cosb - косинусы углов, образованных лучом l с положительным направлением осей координат Ох и Оу).

 

Рис. 14.1.

         При перемещении в данном направлении l точки М(х,у) в точку М/(х + Dх, у + Dу) Î w функция u = f(x,y) получает приращение

 

Du = f(х + Dх, у + Dу) - f(x,y),            (14.1)

 

которое называется приращением функции u в данном направлении.

Если ММ/ = Dl есть величина перемещения точки М, то из DМРМ/ получаем

                                                                                             (14.2)

Следовательно,  Dl u = f(х + Dх, у + Dу)  -  f(x,y).

Определение 14.1. Под производной  функции u в данном направлении к величине перемещения при условии, что последняя стремится к нулю, т.е.

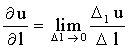                                               .                                             (14.3)

 

         Тогда частные производные ,  можно рассматривать как производные функции u в положительных направлениях осей координат Ох и Оу.  Производная  дает скорость изменения функции в направлении l.

         Пусть u = f(x,y) - дифференцируема. Тогда, используя формулу полного дифференциала, будем иметь

,

где e1 ® 0, e2 ® 0 при Dх ® 0, Dу ® 0. Тогда в силу соотношений (14.2) получаем

и, переходя к пределу  при Dl ® 0 , что то же самое, что и  Dх ® 0, Dу ® 0, имеем

                                      .                                          (14.4)

З а м е ч а н и е. Пусть u=f(x,y,z). Ее производная в направлении

 l = íСos a, Cos b, Cos gý будет .

 

14.2. Градиент и его свойства

 

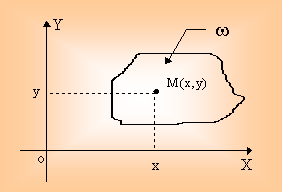
Определение 14.2. Говорят, что в данной области w определено скалярное поле, если для каждой точки М Î w задан некоторый скаляр (т.е. число)

                                                      U = f(M).                                                    (14.5)

 

         Следовательно, U есть числовая функция точки.

Примерами скалярных полей являются:

- температурное поле (т.е. распределение температуры в нагретом теле);

- концентрация вещества в растворе.

Рис. 14.2.

         Пусть w (т.е. область) расположена на плоскости Оху; тогда любая ее точка определена координатами (х,у). При этом плоское скалярное поле (14.5) может быть записано в виде

                   U = f(х,у),  ((х,у) Î w).

         Аналогично в пространстве Охуz

                   U = f(х,у,z),  ((х,у,z) Î w)

Таким образом, понятие скалярного поля представляет собой физическую трактовку функции нескольких переменных.

 

 

Определение 14.3. Будем говорить, что в данной области w определено векторное поле, если для каждой точки М Î w задан некоторый вектор

                                                                                                         (14.6)

 

Примеры.

         1. Поле скоростей в данный момент времени точек потока жидкости.

         2. Силовое поле, создаваемое некоторым притягивающим центром.

         Для плоского векторного поля (14.6) мы будем иметь вектор-функцию

                            a = F(x,y),   ((х,у) Î w)                                                   (14.7)

Отсюда, переходя к координатам вектора а, получим

                            аx  = F1(x,y),    аy  = F2(x,y).

         Таким образом, задание плоского векторного поля (14.7) равносильно заданию двух скалярных полей.

 

 

         Аналогично для случая пространственного векторного поля

                            a = F(х,у,z),  ((х,у,z) Î w);

                            аx = F1(x,y,z),

                            аy = F2(x,y,z),                                                                   (14.8)

                            аz = F1(x,y,z).

В этом случае векторное поле эквивалентно трем скалярным полям.

         Множество точек М, для которых скалярное поле (14.5) сохраняет постоянное значение f(M) = const, называется поверхностью (или линией) уровня скалярного поля (изоповерхностью).

 

 

Рис. 14.3.

 

Рис. 14.4.

 

 

 

 

 

 

 

 

 

 

 

 

 

т.е. изоповерхность -  это множество всех точек пространства Оxyz, где данная функция имеет одно и то же значение. 

 

 

Определение 14.4. Пусть U=f(х,у) - дифференцируемая плоское скалярное поле (функция двух переменных). Тогда вектор

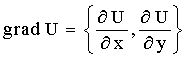                        (14.9)

называется градиентом поля.

 

Или подробнее 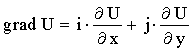   ,  где i,j - единичные вектора, направленные по осям Ох и Оу (координатные орты).

         Аналогично для пространства.

 

Пусть U=f(х,у) - пространственное скалярное поле, тогда его градиент есть вектор          .

Таким образом, скалярное поле порождает векторное поле - поле градиентов.

         Под производной скалярного поля в данном направлении l понимаем

Производная   представляет собой скорость изменения поля в данном направлении.

 

14.3. Частные производные высших порядков

 

         Пусть z=f(x,y). Тогда   и  - частные производные по  переменным х и у . В некоторых случаях существуют снова от этих функций частные производные, называемые частными производными второго порядка (или просто вторыми производными):

 ,    ,

 ,     и т. д.

         Можно определить частные производные любого порядка, если все рассматриваемые функции непрерывны как функции своих независимых переменных,  при этом  результат частного дифференцирования не зависит от последовательности дифференцирования.

Например, если  и  непрерывны, то имеет место равенство

.

Пример.  Пусть z = xy,    ( x>0 ).

                   Имеем

  ; ;

;  .

 

14.4. Признак полного дифференциала

 

         Если u = f(x,y) - дифференцируема, то полный дифференциал имеет вид:

                                      du = P(x,y)dx + Q(x,y)dy,                                     (14.10)

где   ,  .

         Возникает обратная задача:  при каких условиях выражение

                                      P(x,y)dx + Q(x,y)dy,                                              (14.11)

где функции P(x,y), Q(x,y) непрерывны со своими производными первого порядка, является полным дифференциалом функции u.

 

Теорема 14.1. (Необходимое условие)Для того, чтобы (14.11) являлось в некоторой области G полным дифференциалом некоторой функции u=F(x,y), необходимо, чтобы в этой области

                                        (х,у Î G)                                                       (*)

(*) - условие полного дифференциала.

 

Д о к а з а т е л ь с т в о:

         Пусть (14.11) - полный дифференциал функции u = F(x,y). Имеем

                                      .                                                  (14.12)

Отсюда в силу единственности дифференциала получим

                                      ,  .

         Дифференцируя первое по у, а второе - по х, будем иметь

                                      ,  .

Но, так как для непрерывных функций результат дифференцирования не зависит от порядка дифференцирования, то получаем (*)

.

С л е д с т в и е. Если условие (*) не выполнено, то выражение (14.4) не является полным дифференциалом.

 

Пример:

                   а) ydx - xdy

                   б) ydx+xdy

Проверить, являются ли полными дифференциалами а) и б).

                   а) ,  - не является.

                   б) P=y, Q=x,   

                    d(xy)=ydx+xdy.

 

 

 15. Экстремумы функции нескольких переменных

15.1. Максимум и минимум функции нескольких переменных

 

         Напомним, что под окрестностью точки плоскости понимается внутренность любого прямоугольника, окружающего эту точку, исключая саму точку (проколотая окрестность).        

         В пространстве это будет произвольный параллелепипед, содержащий эту точку за вычетом самой точки.

 

Определение 15.1.   Максимумом (строгим) функции  f (x, y)  называется такое значение   f(x1, y1)     этой функции, которое больше всех ее значений  f(x, y),  принимаемых данной функцией в точках некоторой окрестности точки  О(х1, у1). (Окрестность может быть весьма малой по своим линейным размерам).

 

Определение 15.2.    Минимумом (строгим) функции  f (x,  y)  называется такое значение  f (x2,y2), которое меньше всех ее значений  f (x,y),  принимаемых данной функцией в  точках некоторой окрестности  О (х2, у2).

 

         Максимум или минимум функции f (x, y)  называется экстремумом этой функции. Точка, в которой достигается экстремум, называется точкой экстремума (точка минимума, точка максимума).

         Аналогично определяется экстремум функции  f (x, y, z)  и т.д.

 

Теорема 15.1. (Необходимый признак экстремума функции нескольких переменных). В точке экстремума функции  нескольких переменных каждая ее частная производная первого порядка либо равна нулю, либо не существует.

 

Д о к а з а т е л ь с т в о.    Пусть  u = f (x, y)  и f (xo, yo) - ее максимум (для минимума  рассуждения аналогичны). Зафиксируем одну из переменных, например,  у,  полагая  у = уо,  тогда получим функцию одной переменной   U1 = f (x, yo),  которая, очевидно, будет иметь максимум   при  х = хо.  Отсюда,  на основании теории экстремума одной переменной,                                  получаем, что 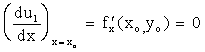           или        не существует.

         Пусть теперь у=уо, а хо- фиксируем, тогда     или не существует.

 

С л е д с т в и е.    В точке экстремума  Мо (хо, уо)  дифференцируемой функции  f (x, y)  выполнены  равенства      

Для  U = f(x, y, z)    в точке  Мо (хо ,уо, zо) будет выполнено условие .

 

З а м е ч а н и е.   Точку, в которой частные производные первого порядка либо не существуют, либо  равны нулю, называют критической.

Т.е.  экстремумы функции нескольких переменных могут достигаться лишь в критических точках.

 

Пример 15.1.   Покажем, что указанные выше условия не являются  достаточными.  Пусть    z = f(x, y) = x × y   тогда  имеем

Следовательно,      Однако точка  0(0,0)  не является точкой экстремума, т.к. в  любой окрестности точки 0 (о,о)  имеются точки

                                  A  (e,e)   и    B(- e, e)    " e > 0 :

                                  f(A)  =  e2  > 0 =  f(0)     и  f(B) = - e2 < f(0).

 

15.2.      Абсолютный экстремум

 

Определение 15.3.   Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции. (Соответственно, абсолютный минимум, абсолютный максимум).

 

Теорема 15.2.   (Вайерштрасс)  Функция, непрерывная в ограниченной и замкнутой области, достигает в этой области своего наименьшего и своего наибольшего значения. (Без доказательства)

 

Теорема 15.3.   Абсолютный экстремум функции в данной области достигается либо в критической точке функции, принадлежащей этой области, либо в граничной точке области. (Без доказательства)

 

Пример 15.2. Для функции   z = x × y   найти абсолютный экстремум в треугольной области  S  с вершинами   О(0,0),  А(1,0),  В(0,2).

Определим   

 

Рис. 15.1.

         Критическая точка  O(0,0)  Π S.   На участке  ОА  имеем  у = 0  (0 £  х £ 1) и тогда z = 0.

         Аналогично  ОВ:  х = 0  (0 £ у £ 2) Þ z = 0.

Наконец, отрезок  АВ  имеет уравнение       или   у = 2 - 2х    (0 £ х £ 1).

Отсюда     z = x ×  y = 2x - 2x2  .

Имеем      ,  т.е.  при   и  т.к.         ,   то  в точке      функция  Z   достигает своего наибольшего значения       на отрезке     АВ.

   

 

 Итак,  наименьшее значение    z  в  S  есть  m=0  и оно реализуется в точках отрезков  ОВ и ОА, составляющих часть границы  Г.

                                        достигает в точке  

 

 

15.3.    Метод наименьших квадратов

 

         В различных исследованиях по данным результатов исследований, часто возникает необходимость построения эмпирических формул, составленных по этим наблюдениям.

     Одним из наилучших способов получения таких формул является метод (способ) наименьших квадратов.

     Пусть по результатам опыта нам нужно установить зависимость между двумя величинами   х  и  у, где, например,

         х - стоимость строительства объекта;

         у - накладные расходы.

По результатам наблюдения составим таблицу:

 

 

Xi

x1

x2

x3

...

xn

Уi

y1

y2

y3

...

yn

 

Нужно теперь установить функциональную зависимость  у = f(x).

         Нанесем результаты наблюдений на координатную плоскость.

 

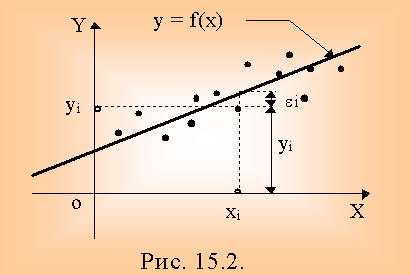         В данном случае естественно предположить, что зависимость линейная (т.е. все точки расположены около прямой).

 

     Т.е.    у = ах + b       (*)

где  а  и  в  - некоторые постоянные коэффициенты, подлежащие опреде-лению.

 

 

         Представим  (*)  в виде     ах + b - y = 0                           (**)

     Так как точки лежат приблизительно на этой прямой, то эта зависимость приближенная. И, если подставить точки наблюдений в (**), то получим равенства:

 

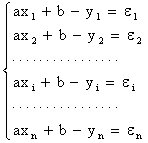                                                          (15.2)

 где  числа   ei (i=1¸n)  называются погрешностями и, вообще говоря, не равные нулю.

         Способ наименьших квадратов состоит в том, что нужно подобрать  а  и  b  таким образом, чтобы  ei  были бы по возможности малыми по абсолютной величине, а лучше сказать, чтобы сумма квадратов погрешностей была бы минимальной. Т.е. потребуем, чтобы

                                                                          (15.3)

тогда  S(a,в)  можно рассматривать как функцию двух переменных по  а  и  b и можно ее исследовать на экстремум  ( определить минимум), т.е.

                             .

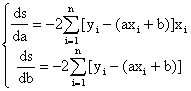                                                                                 (15.4)

 

Приравняем эти частные производные к нулю, получаем линейную систему двух уравнений с двумя неизвестными  а  и  b :

 

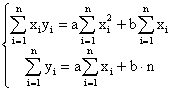                                                                                     (15.5)

     Система  (15.5)  называется нормальной системой способа наименьших квадратов.

     Решая эту систему относительно  а  и  b, находим числа  а  и  b и затем подставляем их в (*).

 

Пример:

         Пусть имеем результаты наблюдений:

 

Xi

-2

0

1

2

4

Уi

0.5

1

1.5

2

3

 

Определим а и в   в уравнениии       у = ах +b

 

 

Нормальная система

 

             . 

Тогда     у = 0,425х + 1,175.

 

 

Назад  Далее