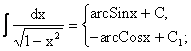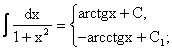Глава III

Интегральное исчисление

 

1. Определение и свойства неопределенного интеграла

 

1.1. Первообразная и неопределенный интеграл

 

         Интегральное исчисление решает обратную задачу по отношению к дифференциальному исчислению: по данному дифференциалу, а следовательно, и производной неизвестной функции F(x), требуется определить эту функцию.

         Пусть известна функция f(x) и нужно по данной функции  определить F(x) таким образом, чтобы

dF(x) = f(x)dx

или соответственно                      .                                      (1.1)

Для простоты будем предполагать, что равенство (1.1) выполнено на некотором промежутке  (конечном или бесконечном).

 

Определение 1.1.  Пусть функция f определена на некотором промежутке, т.е. на отрезке, интервале или полуинтервале числовой оси. Функция F, определенная на этом же промежутке  называется первообразной функции f , если выполнено (1.1) для каждого х из указанного промежутка.

 

         Очевидно, что если F является первообразной для f на  <a,b>, то функция F+ C  (C-Const ), также является первообразной для f на <a,b>.

         Действительно,

                                      [F(x) + C]' = F'(x) = f(x), х Î<a,b>.                           (1.2)

 

Теорема 1.1.   Две различные первообразные одной и той же функции, определенной на некотором промежутке <a,b>, отличаются друг от друга на постоянное слагаемое.

 

Д о к а з а т е л ь с т в о:

 

         Пусть F и Ф - две первообразные для f на некотором промежутке <a,b>, т.е. F'(x) = f(x) и Ф'(x) = f(x), но тогда

                                      [F(x) - Ф(х)]' = 0, х Î<a,b> и, следовательно,

F(x) = Ф(х) + С тогда они отличаются на некоторую константу.

 

         Геометрическая интерпретация.

 

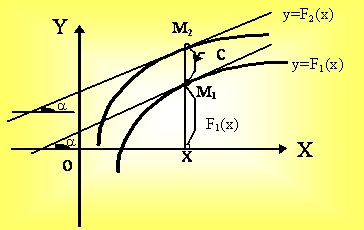у = F(x)+C

tga  = F'1(x) = F'2(x) = f(x),

F1(x) - F2(x) = C.

 

С л е д с т в и е. Прибавляя к какой - либо первообразной F(x) для данной функции, определенной на <a,b>, всевозможные постоянные С получим все первообразные для f(x).

 

                         

Рис. 1.1

 

1.1.2.  Неопределенный интеграл

        

В дальнейшем мы будем предполагать, если явно не оговорено противное, что рассматриваемая функция f(х) определена и непрерывна на некотором конечном или бесконечном промежутке <a,b>.

         Введем теперь основное понятие интегрального исчисления - понятие неопределенного интеграла.

 

Определение 1.2. Совокупность всех первообразных функции f, определенных на некотором промежутке <a,b>, называется неопределенным интегралом от функции f на этом промежутке и обозначается

                                                                  .                                                            (1..3)

- называется знаком интеграла;

f(x) - называется подынтегральной функцией;

f(x)dx - называется подынтегральным выражением;

 - называется функцией общего вида, дифференциал которой равен подынтегральному выражению f(x)dx, и, следовательно, производная по переменной х равна подынтегральной функции f(x) во всех точках <a,b>.

Если F - какая-либо первообразная функции f на  <a,b>, то  пишут

                                                   .                                              (1.4)

Замечание. Здесь записано равенство между множествами и правильнее было бы

 

 

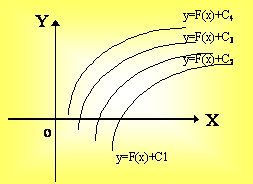
         Геометрически неопределенный интеграл

y = F(x) + C

  представляет собой семейство “параллельных” кривых.

 

 

 

 

Рис. 3.2

 

 

Пример.

                   а) ,

                   б) ,

то есть dx или dz указывают, по какой переменной следует искать первообразную.

 

1.1.3. Основные свойства неопределенного интеграла

        

Основываясь на формуле (2.2), выведем основные свойства.

 

         1. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции.

,

                                                                 .                                                        (1.5)

         2. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции  равен самой этой функции с точностью до постоянного слагаемого.

В самом деле, пусть

,

где j/(х) - непрерывна. Тогда j(х) очевидно является первообразной для j/(х). Поэтому

.

Замечание. В формулах (1.4) и (1.5) знаки  и d, следующие друг за другом в том или ином порядке, взаимно уничтожают друг друга, если не считать константы.

(то есть интегрирование и дифференцирование являются взаимно обратными математическими операциями).

 

         3. Отличный от нуля постоянный множитель можно выносить за знак неопределенного интеграла.

Ecли k = const, тогда

                                              .                                          (1.6)

Д о к а з а т е л ь с т в о:

 

         Пусть f(x) имеет первообразную F(x)+C.

Рассмотрим k×F(x)+k×C - первообразная, тогда [k×F(x)+k×C]/= k×F/(x)+0=k×f(x), так как F/(x)=f(x) с точностью до константы.

 

Замечание. При k=0 формула (1.6) неверна, так как левая часть в этом случае представляет собой производную постоянной, а правая тождественно равна нулю.

 

 

         4. (Аддитивность интеграла относительно функций). Неопределенный  интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме неопределенных интегралов от этих функций.

         Пусть

,, и, следовательно,

 , ,.

         Положим F=F1+F2-F3, тогда

, то есть F является первообразной для f1 + f2 - f3, поэтому

.

 

 

.

 

1.1.4. Таблица простейших неопределенных интегралов

        

Операция нахождения неопределенного интеграла есть обратная операция по отношению к операции дифференцирования. Поэтому нетрудно получить таблицу простейших интегралов. Обращая формулы дифференцирования, получим

 

 

1.

,

,(m¹-1);

2.

,

,(x¹0);

3.

,

;

4.

,

,(a>0,a¹1);

5.

,

;

6.

,

;

7.

,

;

8.

,

;

9.

,

 

10.

,

11.

,

 

12.

13.

 

;

13/.

 

;

14.

 

15.

 

16.

 

.

 

 

2. Методы интегрирования (основные)

2.1. Независимость вида неопределенного интеграла от выбора аргумента

        

Пусть х - независимая переменная, а f(х) - непрерывная функция на данном промежутке, F(x) - ее первообразная, то есть F/(x)=f(x). Имеем

                                    .                                                              (2.1)

         Положим теперь u = j(x), где опять предположим, что j/(х) - непрерывна, то есть j(х) - непрерывно-дифференцируемая функция.

Рассмотрим

                                    .                                                            (2.2)

         В таком случае сложная функция

F(u)=F(j(x)) является первообразной для подинтегральной функции интеграла (2.2)

                             

dF(u) = F/(u)du = f(u)du                           (2.3)

и, следовательно,

                                           .                                    (2.4)

Поэтому

,

где F/(u)=f(u).

         Таким образом, из справедливости (2.1) следует (2.4). На основании этого получаем обобщенную таблицу простейших интегралов.

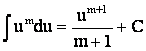 (m¹-1)

 и т.д., где u - любая непрерывная дифференцируемая функция.

И тогда мы можем значительно расширить таблицу простейших интегралов.

 

Пример: Пусть

.

         а) заменим х на Sinx, получим

, то есть

.

         б) заменим х на lnх

         или

.

         Теперь понятно, почему важно уметь проводить f(x)dx=g(u)du, где u есть некоторая функция от х и g - функция, более простая для интегрирования, чем f.

         Отметим несколько преобразований, полезных в дальнейшем:

                   1. dx = d(x + b) , b = const

                   2. , a- const ¹ 0

                   3. , a,b – const ¹ 0

                   4.

                   5.

                   6.

                   7. j/(x)dx = dj(x) (*)

Пример.

                   1. .

                   2. .

 

2.2. Понятие об основных методах интегрирования

        

а). Метод разложения.

        

Пусть f(x) = f1(x) + f2(x). Тогда на основании свойства 4

.

f1, f2 стараемся подобрать так, чтобы интегралы брались непосредственно.

 

Пример:

                   1. ?

Воспользуемся .

.

                   2.   =

=.

        

б). Метод подстановки (введение новой переменной)

 

         Так как неопределенный интеграл не зависит от выбора  аргумента и, учитывая, что 

dx = j/(t)dt,

получаем формулу замены переменной в неопределенном интеграле

                                    .                                                  (2.5)

         То есть интеграл, стоящий в правой части,  может оказаться проще интеграла в левой части.

Пример.

         1. .

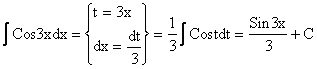         2. .

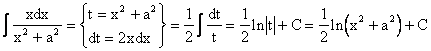         3. .

Практические занятия

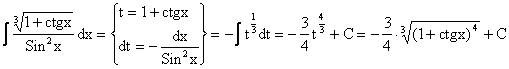в) Метод интегрирования по частям

 

         Пусть u и v - непрерывно дифференцируемые функции от х.

                   d(u×v) = udv + vdu.

Отсюда

udv=d(u×v)-vdu.

 

Интегрируя обе части этого уравнения, получим

 

или

                                             .                                     (2.6)

         Эта формула называется формулой интегрирования по частям.

 

Пример.

                   1..

                   2. .

 

2.3. Интегрирование рациональных дробей с квадратным знаменателем

 

         Нужно вычислить интеграл вида

,     где

Р(х) - целый многочлен; а,b,c - const, a ¹ 0.

Разделив Р(х) на знаменатель, получаем

.

Теперь все сводится к вычислению

                                                         .                                      (2.7)

Примеры.

         Выведем два основных интеграла

I.    (a¹0)

II.                (a¹0).

         Тогда имеем

  (а¹0).

III. .

        

Результаты записать в таблицу основных интегралов.

        

Основной прием вычисления интегралов (2.7) состоит в следующем :

квадратный трехчлен а×х2 + b×x + c дополняют до полного квадрата, если он не является таковым.

Если m = 0, то (2.7) сводится либо к I, либо к II.

Если m ¹ 0, то (2.7) сводится к I и III, либо к II и III.

Рассмотрим это на примерах:

1. .

2.

.

а). Понятие о методе неопределенных коэффициентов

        

Если квадратный трехчлен имеет действительные различные корни х1, х2, то для вычисления (2.7) можно воспользоваться разложением подынтегральной функции на простейшие дроби:

 º .

         Для определения коэффициентов А и В приведем правую часть тождества к общему знаменателю и, приравнивая числители, получим, что коэффициенты при одинаковых  степенях х должны быть равны.

m×x + n = A×(x - x2) + B×(x - x1)

тогда, отсюда следует

.

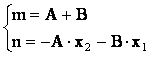Пример.

   ?

.

 

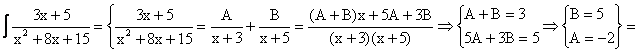
Для качественного усвоения темы необходимо практическое занятие. Интегрирование рациональных дробей.

2.4. Интегрирование простейших иррациональностей

 

         1. Если подынтегральная функция содержит лишь линейную иррациональность

 (а ¹ 0),

то полезна подстановка

.  (*)

         2. Интеграл от простейшей квадратной иррациональности

вычисляется с помощью дополнения квадратного трехчлена до полного квадрата и сводится к одному из двух интегралов типа

,

которые вычисляются подстановкой Эйлера:

I. (a¹0)

, где t- новая переменная.

То есть

х2 + a = t2 - 2×t×x + x2   или  a = t2 - 2×t×x.

 

Возьмем дифференциал от обеих частей, получим

da = 0 = 2tdt - 2xdt - 2tdx или

tdx = (t - x)dt, тогда

, то есть .

Таким образом,

.

                                               .(a¹0).                       (2.9)

II. .                                                             (2.10)

 

З а м е ч а н и е. Необходимо (2.9) и (2.10) дописать в таблицу интегралов.

 

2.5. Интегрирование тригонометрических функций

1. Универсальная замена

          Рассмотрим интеграл вида

                                                    .                                       (2.11)

 Подстановка 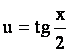 сводит интеграл  (3.1) к интегралу от рациональной дроби.

,

,

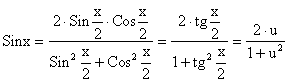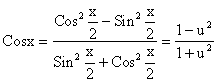то есть   х = 2×arctgu, ,

поэтому

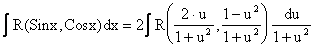                               .                         (2.11\)

Пример.

.

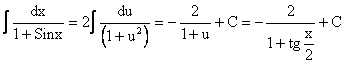З а м е ч а н и я.

        

1. С принципиальной точки зрения интегралы вида (3.1) всегда можно привести к интегралам от рациональной дроби указанным способом, но практическое применение иногда приводит к громоздким вычислениям.

         2. Иногда гораздо полезнее делать замены вида

u = Sinx,   u = Cosx,    u = tgx.

Рассмотрим эти методы на примерах.

1.

=.

2.

.

        

         3. Другие примеры с использованием

Sin2x + Cos2x = 1

        

                   .

Сравните 2 и 3.

 

 

2. Интеграл вида:

                                      .                                                  (2.12)

         Пусть m и n - рациональные числа. Тогда (2.12) с помощью подстановки (см. замечание 2) сводится к интегралу от дифференциального бинома.

         Пусть u = Sinx, тогда

du = Cosxdx, , и тогда

                                         .                            (2.13)

         а) В частном случае, когда m и n - целые (даже не обязательно положительные), то тогда целесообразно делать подстановки ( замечание 2). Например, если m = 2×n + 1 (соответственно n = 2×k+1), то есть нечетное число, то можно делать подстановку вида u = Cosx (u = Sinx):

(получаем рациональную дробь).

         Аналогично, если

.

         б) m>0, n>0, четные (или одно из них 0).

Тогда целесообразно применить

,   .

Пример.

.

 

 

 

         3. Интегралы вида

 

, ,.                    (2.14)

При вычислении интегралов (3.4) нужно вначале воспользоваться формулами

.

Пример.

                   .

 

2.6. Интегралы от некоторых трансцендентных функций

 

         К этому виду относятся, например, интегралы:

,   ,

,  ,

,      (n - целое).

         Все интегралы такого типа вычисляются, вообще говоря, с помощью интегрирования по частям (повторного интегрирования по частям).

 

Пример.

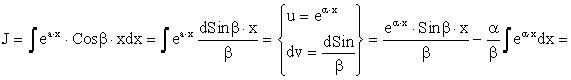
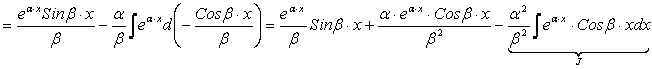  Þ

 

.

3. Замечания об интегралах, не выражающихся через элементарные функции

 

Теорема 3.1. (Коши). Всякая непрерывная функция имеет первообразную. То есть пусть f(x) - непрерывна, определена на (a,b) Þ $ F(x) : F/(x)=f(x) и тогда

.

Но, тем не менее, не решается вопрос о том, как найти первообразную с  помощью конечного числа известных операций над элементарными функциями. Более того, имеется ряд непрерывных элементарных функций, интегралы от которых не являются элементарными функциями. Такие интегралы называются “неберущимися”.

 

Примеры.

,   ,   ,  

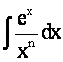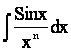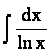
и ряд других.     

 

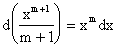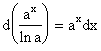   Назад  Далее