4. Определенный интеграл
4.1. Определение интеграла по Риману
Пусть f(x) - функция, непрерывная на данном отрезке [a,b], где a < b (a>b), и
F(x) - некоторая первообразная при хÎ[a,b].
Разобьем отрезок [a,b] на n частей
а = х0 < x1 < x2 < ... < xn = b. (4.1)
Обозначим длину отрезка [хi-1, хi] (i = 1¸k) через Dхi = хi - хi-1.
Тогда величина ![]() (4.2)
(4.2)
называется мелкостью разбиения.
Зафиксируем произвольным образом точки
xiÎ[xi-1,xi], i=1,2,...,k
и составим сумму
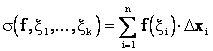 .
(4.3)
.
(4.3)
Суммы вида (4.3) называются интегральными суммами Римана.
Определение 4.1.
Функция f называется интегрируемой (по Риману) на отрезке [a,b],
если существует такое число А, что любой
последовательности разбиений отрезка [a,b],
у которой ![]() и для любого выбора
точки xiÎ
[хi-1,хi],
(i=1¸n)
выполняется равенство
и для любого выбора
точки xiÎ
[хi-1,хi],
(i=1¸n)
выполняется равенство
![]() , (4.4)
, (4.4)
где
![]() (i=1¸k,
n=1,2, ...).
(i=1¸k,
n=1,2, ...).
Если выполнены все условия определения 4.1, то число А назовем (Римановым) определенным интегралом функции f на отрезке [a,b] и будем обозначать
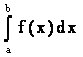 .
(4.5)
.
(4.5)
Таким образом,
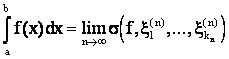 ,
,
где ![]() ,
,
или подробно
 . (4.6)
. (4.6)
Определение 4.2.
Число А называется определенным интегралом функции f на отрезке [a,b], если для
"
e>0
$
d=d(e)>0
: для любого разбиения ![]() [a,b], мелкость
которого меньше di
dt<d,
каковы бы ни были точки xiÎ[xi-1,xi],
то будет выполнено неравенство
[a,b], мелкость
которого меньше di
dt<d,
каковы бы ни были точки xiÎ[xi-1,xi],
то будет выполнено неравенство
![]() ,
,
где Dхi=хi-хi-1, i=1¸k.
Если F(x) - первообразная, то под определенным интегралом понимается соответствующее приращение первообразной на [a,b], то есть
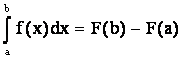 (4.7)
(4.7)
(формула
Ньютона-Лейбница).
Мы докажем эту формулу позже.
Запишем формулу Ньютона-Лейбница в следующем виде
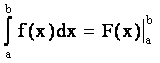 ,
,
где a и b назовем соответственно нижним и верхним пределом интегрирования.
4.2. Свойства определенного интеграла
1. 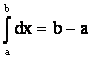 .
.
2. Если f интегрируемая на [a,b] тогда она интегрируемая на любом [a*,b*] Ì [a,b]. Кроме того, будем считать, что для всех f(х), имеющий смысл в точке a, тогда
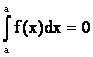 .
.
3. Пусть a<c<b. Если f(x) интегрируемая на [a,c] и [c,b] тогда она интегрируемая и на [a,b], причем
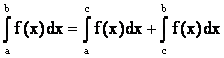 - (aддитивность). (4.8)
- (aддитивность). (4.8)
4. Если функции f и g интегрируемые на [a,b], а a,b - некоторые константы, то их сумма af + bg так же интегрируемая на [a,b]
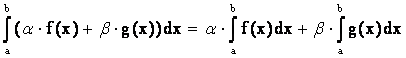 - (линейность).
(4.9)
- (линейность).
(4.9)
5. Определенный интеграл от непрерывной функции не зависит от выбора первообразной для подынтегральной функции.
Д о к а з а т е л ь с т в о:
Пусть F(х) и F1(х) - две различные первообразные непрерывной на [a,b] функции f(x) интеграла
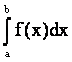 , тогда F1(x)=F(x)+C, но тогда
, тогда F1(x)=F(x)+C, но тогда
 .
.
Тогда мы получаем замечательное следствие
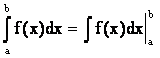 ,
(4.10)
,
(4.10)
где под ![]() понимается одна из
первообразных для f(x).
понимается одна из
первообразных для f(x).
Формула (4.10) устанавливает связь между неопределенным и определенным интегралами.
З а м е ч а н и е. Определенный интеграл - число, неопределенный интеграл - функция.
6. Если f интегрируемая на [a,b], a C - const следовательно c×f также интегрируемая на [a,b] и
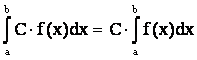 .
.
7. Если f(x), g(x) - интегрируемые на [a,b], их произведение f(x)×g(x) также интегрируемое на [a,b].
8. Если f(x) и g(x) интегрируемые на [a,b] и f(x)³g(x) " хÎ [a,b] Þ
а) 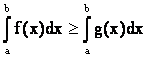 .
.
б) 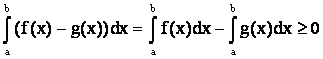 .
.
в) 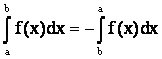 , (a < b).
, (a < b).
9. Если f(x) интегрируемая на [a,b] тогда и çf(x)ç также интегрируемая на [a,b]
 , (a < b).
, (a < b).
4.3. Определенный интеграл с
переменным верхним пределом
Пусть f(x) интегрируемая на [a,b]. Тогда по свойству (2) она интегрируемая на любом отрезке [а,х], где а< х< b, то есть " хÎ[a,b] имеет смысл интеграл
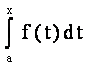 .
.
Пусть F(x) - первообразная f(x) (F/(x)=f(x)), тогда согласно формуле Ньютона- Лейбница имеем
 .
.
Отсюда
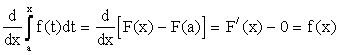 .
.
Следовательно, производная определенного интеграла с переменным верхним пределом по этому пределу равна значению подынтегральной функции для этого предела
 .
.
Таким образом
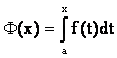
является первообразной для подынтегральной функции f(x).
Отметим, что F(х) - это та первообразная f(x), которая обращается в ноль, когда х = а.
Аналогично 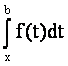 ,
, 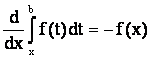 .
.
З а м е ч а н и е.
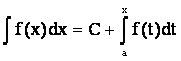 .
(4.11)
.
(4.11)
4.4. Формула Ньютона-Лейбница
Теорема. (Основная теорема интегрального исчисления). Пусть f(x) непрерывна на [a,b] и Ф(х) является какой-нибудь ее первообразной на этом отрезке . Тогда
 . (4.12)
. (4.12)
Д о к а з а т е л ь с т в о:
Положим 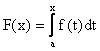 ,
,
но тогда F, Ф - две первообразные одной и той же функции f(x) , то есть
F(x) = Ф(х) + С, а £ х £ b,
то есть
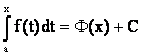 .
.
При х = а следует, что С = -Ф(a).
Таким образом
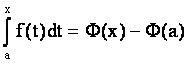 .
.
Полагая здесь х = b, получим (4.12).
Теорема доказана.
4.5. Геометрический смысл
определенного интеграла
Пусть f(x), заданная на [a,b], непрерывна и нужно определить площадь, ограниченную кривой y = f(x) и прямыми х = а, х = b, y = 0.
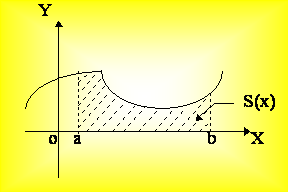
Рис. 4.1
|
Рис. 4.2 |
Si(x) = f(xi)×Dxi, где Dхi = хi - хi-1.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Устремим n ® ¥, Dxi ® 0. Возьмем
![]() .
.
![]() .
.
Но тогда
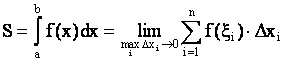 .
.
Таким образом, определенный интеграл от непрерывной неотрицательной функции при a £ b равен площади соответствующей криволинейной трапеции.
4.6. Теорема о среднем для определенного интеграла
Теорема 4.2. (о среднем). Если f(x) интегрируемая на [a,b] и
m £ f(x) £ M, xÎ[a,b] тогда
m×(b-a)
£ 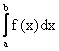 £
M×(b-a).
£
M×(b-a).
Д о к а з а т е л ь с т в о:
Воспользуемся свойствами определенного интеграла:
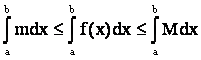 (4.13)
(4.13)
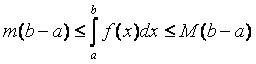 .
.
Следствие. Если f(x) непрерывна на [a,b], тогда существует точка xÎ[a,b] такая, что
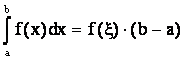 . (4.14)
. (4.14)
Д о к а з а т е л ь с т в о:
Так как f(x)
непрерывна на [a,b] тогда пусть
![]() ,
, ![]()
и, следовательно,
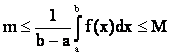 .
.
Таким образом, число

находится между наибольшим и наименьшим значением функции f(x). Но тогда по теореме Коши существует точка xÎ[a,b] такая, что
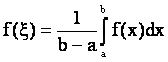 .
.
5. Методы вычисления
определенного интеграла
5.1. Замена переменного
Пусть необходимо вычислить
 ,
,
где f(x) непрерывна на [a,b]
и пусть х = j(t), a £ t £ b, когда а £ j(t) £ b непрерывно-дифференцируемая функция. Тогда
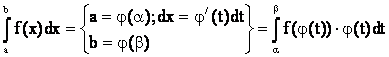 . (5.1)
. (5.1)
Для доказательства (5.1) рассмотрим сложную функцию F(j(t)), где F(x) - первообразная для f(x), то есть F/(x)=f(x). Применяя правило дифференцирования для сложной функции, получим
![]() .
.
На основании формулы Ньютона-Лейбница будем иметь
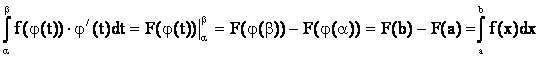 .
.
Пример.
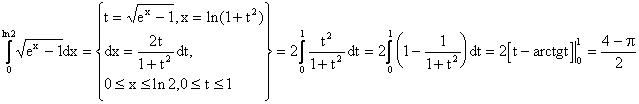
5.2. Интегрирование по частям
Теорема 5.1. (Формула интегрирования по частям для определенного интеграла). Если u = u(x) и v = v(x) непрерывны вместе со своими производными на [a,b], то
 . (5.2)
. (5.2)
Д о к а з а т е л ь с т в о:
Рассмотрим  тогда все интегралы
существуют,
тогда все интегралы
существуют,
так как функции непрерывны.
По формуле Ньютона-Лейбница
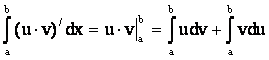 .
.
Отсюда следует (5.2).
Пример.
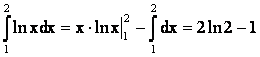 .
.
5.3. Приближенное вычисление определенного интеграла
а). Метод
трапеций
Пусть необходимо вычислить
 ,
,
который вычисляется точно далеко не всегда.
Воспользуемся геометрическим смыслом и получим приближенную формулу для вычисления интеграла.
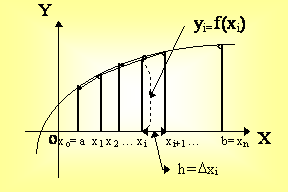
Рис. 4.3
Разобьем
отрезок [a,b]
на n равных частей длиной ![]() ( h - шаг разбиения).
( h - шаг разбиения).
Тогда точки разбиения хi = х0+i×h, a yi = f(xi), i = 0,1, ... , n дадут нам n трапеций с основаниями yi = f(xi) и высотой h.
Суммируя площади этих трапеций, будем иметь формулу трапеций для вычисления приближенного интеграла
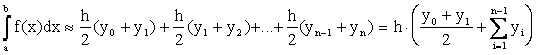 . (5.3)
. (5.3)
б) метод Симпсона
Иногда лучшее приближение дает другая формула, профиль криволинейной трапеции полоски (трапеции) считать параболическим.
Разделим [a,b] на n = 2×m частей.
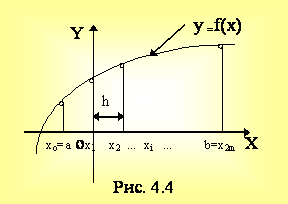
И на каждом участке аппроксимируем нашу кривую
y = f(x) параболой
y = A×x2 +B×x + C.
(См.Рис. 4.5.)
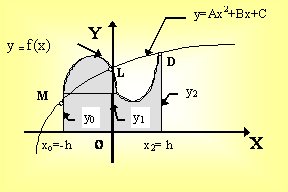
Например, если h мало, то кривую y = f(x)
Можно заменить параболой
y = A×x2+ B×x + C, проходящей через точки
М(х0,у0), L(x1,y1), D(x2,y2).
Но нам нужно определить коэффициенты А,В,С для параболы.
С одной стороны
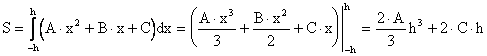 .
(5.4)
.
(5.4)
С другой стороны, если х0 = -h, тогда A×h2 - B×h + C = y0,
при x1 = 0 получаем C = y1,
и x2 = h - A×h2-B×h+C = y2
то есть y1 = C, a ![]() .
.
Тогда подставим полученные значения в (5.4), получим
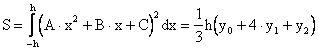 .
.
Но так мы можем аппроксимировать на любом промежутке [a,b] любого разбиения
 .
.
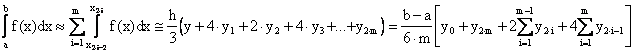
(Формула Симпсона).
5.4. Несобственные интегралы
При определении определенного интеграла всегда предполагалось, что промежуток интегрирования [a,b] - конечен, а f(x) - подынтегральная функция - определена и непрерывна на [a,b]. Такой определенный интеграл называется собственным.
Если хотя бы одно из условий нарушено, то интеграл называется несобственным определенным интегралом.
1. Пусть f(x) - непрерывная при хÎ[а,¥), тогда
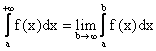 . (5.5)
. (5.5)
Если предел (5.5) существует, то говорят, что несобственный интеграл является сходящимся, в противоположном случае интеграл называется расходящимся.
Если F(х) - первообразная для f(x), тогда
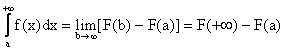 . (5.6)
. (5.6)
(5.6) - обобщенная формула Ньютона-Лейбница.
Пример.
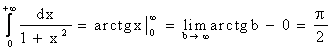 .
.
2. Пусть f(x) непрерывна , хÎ[a,b), а в точке b терпит разрыв, тогда
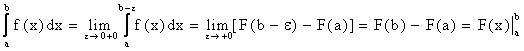 .
.
Пример.
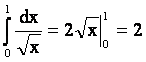 .
.
6. Приложения
определенного интеграла
6.1. Площадь плоских фигур
Рассмотрим приложения определенного интеграла для вычисления площадей некоторых плоских областей.
Пусть требуется определить S - площадь криволинейной трапеции, ограниченной графиком функции y = f(x), отрезком a £ x £ b и x = a, x = b на основании геометрического смысла определенного интеграла
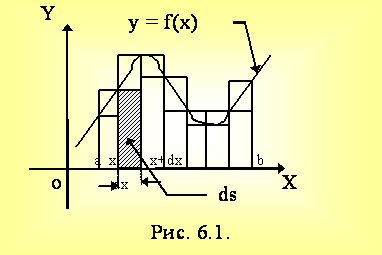
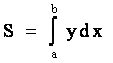 , (6.1)
, (6.1)
где y = f(х).
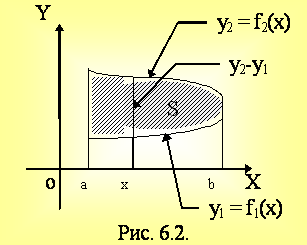
Пусть y1 = f1(x), y2 = f2(x) (y2 ³ y1), x = a, x = b. f1(x), f2(x) ³ 0
при xÎ[a,b].
Тогда 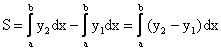 .
.
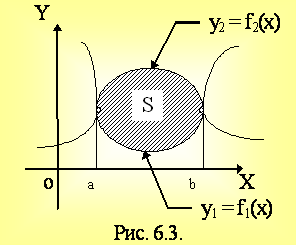
Если f1(x) = y1, f2(x) = y2
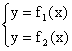 ;
; ![]() - решение системы. Тогда
так же имеем
- решение системы. Тогда
так же имеем
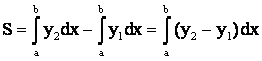 . (6.2)
. (6.2)
6.2. Объем тела вращения
Необходимо определить объем тела Vх, образованного вращением вокруг оси Ох криволинейной трапеции
y =
f(x) (f(x) ³ 0),
отрезок a £ x £ b.
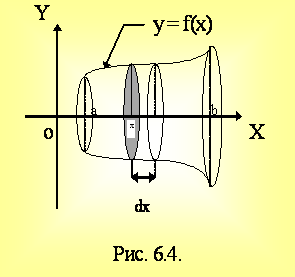
S(x) = p×y2, dVx = p×y2dx
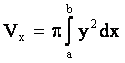 .
(6.3)
.
(6.3)
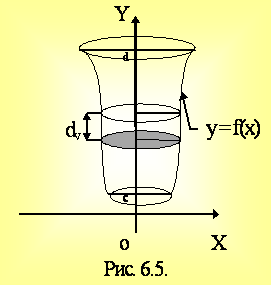
Пусть теперь необходимо определить объем тела Vу, образованного вращением вокруг оси Оу криволинейной трапеции
x = g(y) ³ 0, y = c, y = d
 .
(6.4)
.
(6.4)
6.3. Длина дуги
Определение 6.1. Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной возрастает неограниченно, а длина наибольшего ее звена стремится к нулю.
Если кривая непрерывна и в каждой точке имеет касательную, непрерывно меняющую свое положение от точки к точке, то будем называть такую кривую гладкой.
Пусть y = f(x) - гладкая кривая для xÎ[a,b] и f(x) - непрерывна вместе с f/(x) на [a,b].
Теорема 6.1. Каждая гладкая кривая y = f(x) на [a,b] имеет определенную конечную длину дуги.
Д о к а з а т е л ь с т в о:
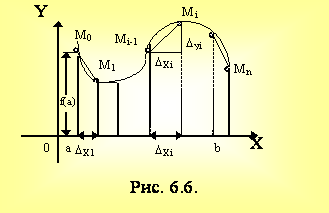 Если спроектировать звенья ломаной на
ось Ох , получим разбиение отрезка [a,b] на систему отрезков Dxi,
Dyi
- приращение данной функции
Если спроектировать звенья ломаной на
ось Ох , получим разбиение отрезка [a,b] на систему отрезков Dxi,
Dyi
- приращение данной функции
y = f(x) на отрезке Dxi, но тогда
![]() .
.
Применим теорему Лагранжа о конечном приращении функции
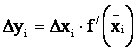 ,где
,где ![]() .
.
И тогда
 .
.
Длина всей ломаной равна
 . (6.5)
. (6.5)
Чтобы найти длину кривой, нужно в последнем уравнении (6.5) перейти к пределу при n ®
¥
и ![]() .
.
Таким образом
 ,
,
но это есть предел интегральной суммы для непрерывной функции
![]() .
.
Тогда
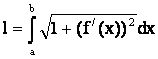 (6.6)
(6.6)
или
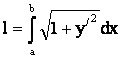 .
.
6.4. Дифференциал дуги
Пусть имеем точку А(a,h) и точку М(х,у).
Тогда длина дуги ÈАМ есть некоторая функция
от переменной х. Согласно (6.6) 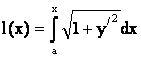
Найдем производную ![]() и, следовательно,
и, следовательно,
![]() . (6.7)
. (6.7)
Это есть формула дифференциала дуги в прямоугольных координатах.
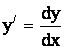 тогда
тогда ![]() .
.
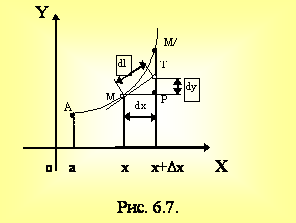
Рассмотрим DМРТ (см. рис. 6.7) по теореме Пифагора для бесконечно малой величины dl имеем
![]() .
.
