7. Понятие о кратных интегралах

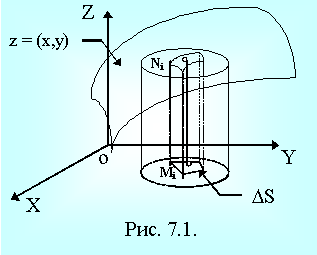
Пусть z = f(x,y) непрерывная функция; требуется определить объем тела, ограниченного некоторой непрерывной поверхностью ( f(x,y) ³ 0 ), а снизу конечной замкнутой площадью S плоскости О_xy.

Тело указанного вида для краткости назовем цилиндром.

V = S×H.

Для вычисления данного цилиндра разобьем основание на DS₁, DS₂, ... , DS_n криволинейных ячеек, высота для каждого DS_i вычисляется f(x_i,y_i) = M_iN_i - аппликата поверхности в выбранной точке.

Тогда DV_i = f(x_i,y_i)×DS_i

и . (7.1)

Эта сумма представляет собой объем ступенчатого тела, приближенно заменяющего данное криволинейное тело.

Формула (7.1) дает возможность найти V с любой степенью точности, если DS_i мало, а число ячеек велико.

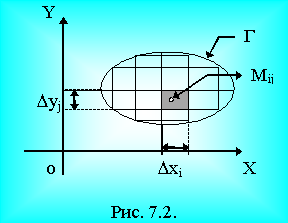
Весьма часто полагают, что DS_ij удобно выбирать прямоугольными со сторонами Dx_i, Dy_j за исключением , возможно, ячеек, примыкающих к Г (границе области S).

DS_ij = Dx_i×Dy_j.

Определение 7.1. Двойным интегралом от функции z=f(x,y), распространенным на данную область S, называется предел соответствующей двухмерной интегральной суммы при неограниченном возрастании элементарных ячеек DS_ij и стремлении их наибольшего диаметра к нулю при условии, что этот предел существует и не зависит от способа дробления области S на элементарные ячейки DS_ij и выбора точек в них.

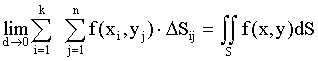. (7.2)

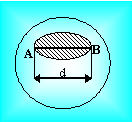
Под d будем понимать длину

наибольшей хорды AB.

Рис. 7.3.

Если dS = dxdy - двухмерный элемент площади в прямоугольных координатах, то имеем

.

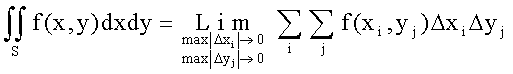7.1. Основные способы вычисления двойного интеграла

Предположим, что область интегрирования S: a£ x£ b, y₁(x) £ y £ y₂(x), где y = y₁(x) и y = y₂(x) - однозначные непрерывные функции хÎ[a,b]. Пусть z=f(x,y) - непрерывная функция в области S.

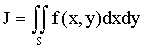. (7.3)

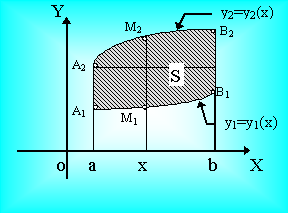
1) Предположим, что f(x,y) ³ 0 в области S. Тогда J - объем цилиндра, ограниченного снизу S, а сверху поверхностью z = f(x,y)

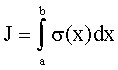. (7.4)

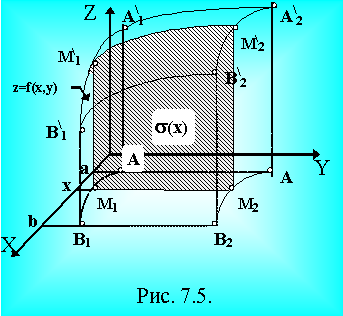
Здесь мы применим так называемый метод сечения.

s(х) представляет собой площадь криволинейной трапеции, ограниченной снизу отрезком у₁ £ у £ у₂ и сверху кривой

z = f(x,y), x = Const.

Поэтому

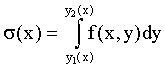(7.5)

и s(х) при наших условиях непрерывна, тогда, подставляя в (7.4) (7.5), получим

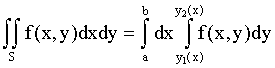. (7.6)

Таким образом, двойной интеграл равен соответствующему повторному интегралу, где при вычислении внутреннего интеграла

х = Const

.

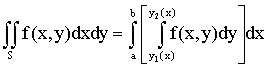Замечание. Если S определена неравенствами c £ y £ d, x₁(y) £ x £ x₂(y), то

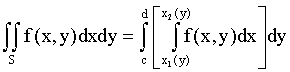. (7.7)

7.1.1. Вычисление площадей при помощи двойного интеграла

Примеры.

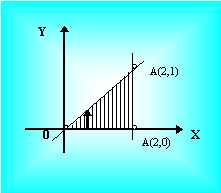
1) 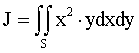, где область S ограничена у = 0, , х = 2 и является стандартной относительно осей О_х, О_у.

.

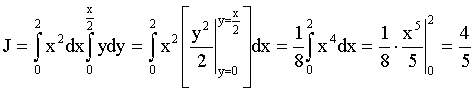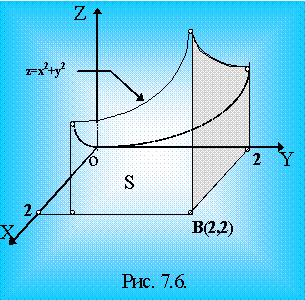
2) Необходимо вычислить объем цилиндра с квадратным нижним

основанием, который ограничен сверху параболоидом вращения

z = x² + y² .

,

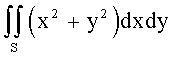где S - квадрат, 0 £ х £ 2, 0 £ у £ 2.

.

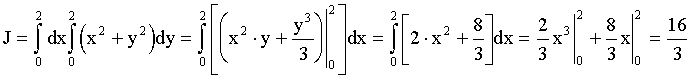3) Изменить порядок интегрирования (самостоятельно).

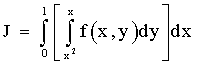
8. Понятие о тройном интеграле

По аналогии с двойным интегралом определяется так называемый тройной интеграл

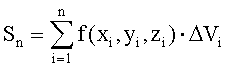, (8.1)

где DV_i - объем i-той ячейки, а S_i- трехмерная интегральная сумма.

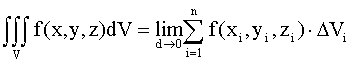. (8.2)

В простейшем случае вычисление сводится к трем квадратурам.

Если область V определена неравенствами a £ x £ b, y₁(x) £ y £ y₂(x), z₁(x,y) £ z £ z₂(x,y), то

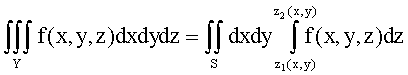. (8.3)

Если у₁(х), у₂(х) - однозначные и непрерывные функции, то

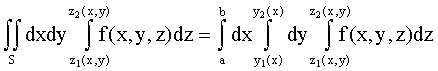. (8.4)

Назад Далее