Глава IV
Дифференциальные уравнения
1.
Понятие о дифференциальном уравнении
Обыкновенным дифференциальным
уравнением nго порядка называется уравнение вида:
F(x, y, y/ ,y//,..., y(n)) = 0.
(1.1)
Примеры.
![]() , y/// =
lnx, ...
, y/// =
lnx, ...
Если уравнение (1.1) имеет вид :
а0(х)×у(n)
+ а1(х)×у(n-1)
+ ... + аn(х)×у =
f(x), (1.2)
где
аi(х) (i=0,1,...,n ) называются коэффициентами
уравнения (линейного); они обычно определены и непрерывны на некотором
общем интервале, а f(x) - правая часть линейного уравнения или свободный член.
Если
f(x) º 0 уравнение (1.2) называется однородным, в противном случае - неоднородным.
Любая функция у = j(х), подставленная в (1.2), обращающая его в
тождество, называется решением этого
уравнения. График решения (то есть кривой у=j(х)) называется интегральной кривой.
Основная
задача - отыскание (поиск) функции у, производная которой равна данной
непрерывной функции f(x), - то есть
сведение к простейшему дифференциальному уравнению у/
= f(x).
Общее решение этого уравнения есть
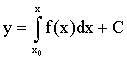 ,
(1.3)
,
(1.3)
где
С - произвольная константа, а 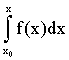 - одна из
первообразных.
- одна из
первообразных.
Выбрав надлежащим образом С, можно
получить любое решение этого простейшего дифференциального уравнения.
З а м е ч а н и е. При интегрировании
дифференциальных уравнений высших порядков появляется несколько произвольных
постоянных.
Пример.
у// = 0
(уравнение второго порядка).
Так как у/ = (у/)/
= 0 тогда у/ = С1,
но тогда ![]() - общее решение.
- общее решение.
Определение 1.1. Общим решением дифференциального уравнения (1.1) называется такое
его решение
y = j(x,C1,C2,...,Cn),
которое
содержит число констант, равное порядку этого уравнения.
Если общее решение записано в
неявном виде F(х,у,С1,...,Сn)
= 0, то его обычно называют интегралом.
Определение 1.2. Всякое решение
дифференциального уравнения , которое получается из общего при определенных
значениях независимых постоянных, называется частным решением этого уравнения.
Пример.
С1
= 2, С2 = -5 тогда у = 2×х - 5 - частное решение
уравнения у//=0.
1.2. Дифференциальные уравнения первого порядка
Уравнение вида
F(x, y, y/) = 0
(1.4)
называется
уравнением первого порядка.
В простейших случаях оно может быть
разрешено относительно
у/ = f(x,y). (
у = j(х,С),
(1.5)
где С - константа.
Геометрически общее решение представляет собой семейство
интегральных кривых.
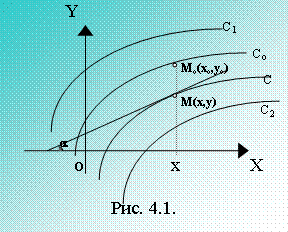 Интегральные кривые обладают
тем свойством, что все касательные в точке М(х,у) имеют наклон tga = f ’(x,y).
Интегральные кривые обладают
тем свойством, что все касательные в точке М(х,у) имеют наклон tga = f ’(x,y).
Если задать точку М0(х0,у0),
через которую должна проходить интегральная кривая, то это требование
называется начальным условием y = у0, х = х0 и тогда
у0 =
j(х0,С0).
Определяется
С - константа; в результате получаем частное интегральное решение у = j(х,С0).
В этом состоит
задача Коши.
Задача Коши. Найти решение у = j(х) дифференциального
уравнения (
З а м е ч а н и е. Нет общего метода интегрирования уравнения
первого порядка. Обычно рассматривают некоторые отдельные типы таких уравнений,
для каждого из которых дается свой способ.
1.3. Уравнения первого порядка с разделяющимися
переменными
Определение 1.3. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными,
если оно имеет вид
f1(x)×g1(y)dx + f2(x)×g2(y)dy = 0, (1.6)
где
f1,f2 - функции переменной х, а g1,g2-
функции переменной у.
Для решения (1.6) разделим его на g1(y)×f2(x),
предполагая, что оно не обращается в нуль.
![]() .
.
Проинтегрировав,
получим
![]() .
(1.7)
.
(1.7)
Тогда
(1.7) - это общий интеграл в неявной форме.
Пример.
у/×х -у = 0.
![]() или
или ![]() .
.
![]() Þ
Þ ![]() .
.
у = С1×х, (х ¹ 0, С1 ¹ 0).
1.4. Однородные дифференциальные уравнения первого порядка
Рассмотрим многочлен
![]() ,
,
он
называется однородным степени n, если
все его члены имеют один и тот же порядок n, то есть для каждого аij×хi×уj имеем i+j=n.
Определение 1.4. Функция Р(х,у) называется однородной степени n, если для любого k - числа - имеет место
тождество
Р(k×х,k×у) = kn×P(x,y).
Пусть
дано уравнение
Р(х,у)dx+Q(x,y)dy=0.
(1.8)
Если P(x,y),Q(x,y) - однородные
функции одной и той же степени n, тогда (1.8) является однородным уравнением первого порядка.
Для
решения таких уравнений пользуются подстановкой ![]() или
или ![]() , которая приводит к уравнению с разделяющимися переменными.
, которая приводит к уравнению с разделяющимися переменными.
Пример.
х2+у2-2×х×у×у/=0.
Предположим, что х×у ¹ 0. Тогда
![]() .
.
![]() следовательно, у = u×x , а отсюда dy = udx+xdu
следовательно, у = u×x , а отсюда dy = udx+xdu
![]()
После
приведения подобных и перегруппировки членов имеем
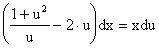
![]()
![]()
![]() Þ
Þ ![]()
![]() следовательно, x2-y2=C1×x - решение.
следовательно, x2-y2=C1×x - решение.
Сделаем
проверку
1.
Если х = 0 тогда C0 = 0 и, следовательно x2 = y2 .
2.
1-u2 = 0 .
Пусть теперь однородное дифференциальное уравнение
имеет вид
у/ = f(x,y) или ![]() .
.
Тогда
dy=f(x,y)dx, то есть при dy стоит коэффициент, равный единице, то есть имеем
однородную функцию нулевой степени: следовательно, f(x,y) должна быть
однородной функцией нулевой степени.
1.5. Линейные дифференциальные уравнения первого порядка
Линейное уравнение имеет вид:
а(х)×у/ + b(х)×y + c(x) = 0, (1.9)
где
а(х), b(x), c(x) - заданные функции.
Если
а(х) ¹ 0, то это уравнение можно
записать в приведенном виде:
у/ + Р(х)×у = f(x), (1.10)
где ![]() ,
, ![]() ,
,
тогда
f(x) - свободный член.
Пусть Р(х) и f(x) в (1.10)
непрерывны на (a,b).
Будем
искать решение в виде y = u×v, где u - ненулевое решение
соответствующего однородного уравнения
u/ + P(x)×u = 0,
(1.11)
a v
- неизвестная функция. Тогда
y/ = u/×v + v/×u.
(1.12)
Подставим
в (1.10) эти выражения. Получим
u/×v + v/×u + P(x)×u×v = f(x) (1.13)
v × (u/+P(x)× u) + u×v/ = f(x)
Учитывая,
что имеет место (1.11), получим
u×v/ = f(x). (1.14)
Следует
u подобрать так, чтобы коэффициент при v был равен нулю.
Из
(1.11) и (1.14) находим u и v, подставляем в y = u×v, причем u есть конкретное
решение, отличное от нуля.
Пример. Необходимо найти частное
решение
x×y/-y = x2.
Начальные
условия:
 .
.
Пусть у = 0 при х
= -1.
Искомое
решение запишем в виде y = u×v.
y/ = u/×v + v/×u.
Подставим в уравнение, имеем
x×u/×v + x×v/×u - u×v = x2.
После приведения подобных имеем
v×(x×u/ - u) + x×u×v/ = x2.
![]() Þ
Þ ![]() следовательно, lnu =
lnx + lnC0.
следовательно, lnu =
lnx + lnC0.
Если
С0 = 1 , значит, u = x.
Но
тогда
x2×v/ = x2 и v = x + C1.
y = x×( x + C1) = x2 + C1×x - общее
решение.
А
если у0 = 0 , то получим 1 + С1×(-1) откуда С1 = 1.
у = х2 + х
- частное решение.
Пример.
(х + у)×у/ = 1.
![]() ,
, 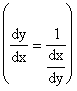 .
.
Пусть
x =
u×v, тогда ![]() и
и
v×u/ + u×v/ = x + y.
Учитывая,
что х = u×v, имеем
v×(u/-v) + u×v/ = y
![]() следовательно, lnu = y,
u = ey,
следовательно, lnu = y,
u = ey,
Так
как ![]() , то имеем
, то имеем![]() .
.
Далее
v = -y×e-y - e-y +
C.
x = u×v = -y-1 + C×ey - общее
решение.
y = -y-1 + C×ey
начальные
условия:
у0 =
0, х0 = 2.
2 = -1 +
С Þ С = 1
х + у + 1 = еу
- частное решение.
Примеры приложений к задачам экономики