2. Дифференциальные уравнения второго порядка

Рассмотрим дифференциальное уравнение второго порядка, разрешенное относительно старшей производной

y^// = f(x,y,y^/). (2.1)

Общее решение

y = j(x,C₁,C₂), (2.2)

где С₁,С₂ - независимые постоянные, и тогда (2.2) представляет собой бесконечную совокупность интегральных кривых. Вообще через каждую точку М₀(х₀,у₀) плоскости О_ху проходит пучок интегральных кривых. Поэтому нужно не только выбрать кривую, но еще и указать ее направление.

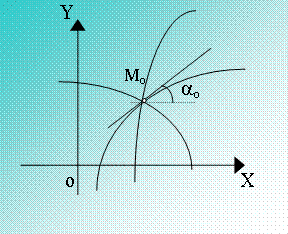
Тогда начальные условия:

у = у₀

y^/_{(х = х0)} = y^/₀

tg a₀ = y^/₀

На основании (2.2) имеем

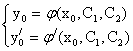(2.3)

Определив С₁ и С₂, подставив в (2.2), получим частное решение у = j(x).

Приходим к задаче Коши.

2.1. Простые случаи уравнений второго порядка

1). Пусть

у^// = f(x) (2.4)

.

2). Пусть

у^// = f(у) (2.5)

Положим у^/ = p. Отсюда, рассматривая р как функцию от у, будем иметь

.

Подставим в (2.5)

.

Разделив переменные, получим

или

. (*)

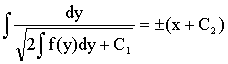Не стоит запоминать эту сложную формулу общего решения (*). Следует усвоить способ интегрирования.

3) Пусть

у^// = f(у^/). (2.6)

Положим у^/ = p следовательно, .

Тогда уравнение (2.6) примет следующий вид:

и ,

.

Определив и вторично интегрируя, можно будет найти у.

Пример.

2×у^/×у^// = 1,

начальные условия:

.

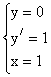Пусть у^/ = р, тогда , следовательно, 2рdp = dx или р₂ = х + С1.

Чтобы определить С₁, используем начальные условия.

p = y^/ , следовательно, 1 = 1 + С₁;

отсюда С₁ = 0 и тогда р₂ = х, следовательно, .

Разделив переменные, получим

.

Начальные условия: у = 0 при х = 1, следовательно, .

Окончательно .

2.2. Случаи понижения порядка

Дано уравнение второго порядка

у^// = f(x,y,y^/). (2.7)

1. Пусть левая часть не содержит х, то есть

у^// = f(y,y^/).

Тогда положим у^/ = р,

.

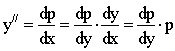Таким образом получим дифференциальное уравнение первого порядка

.

2. Пусть левая часть не содержит у, то есть

у^// = f(х,y^/).

Тогда положим у^/ = р, , и снова получим уравнение первого порядка

.

Пример.

x×y^// = 2×x-y^/.

Начальные условия:

.

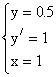Положим у^/ = р, .

.

(*) - это уравнение однородное.

, p = x×u и .

Подставим в (*):

,

, следовательно, .

ln(u -1) = -2lnx + lnC₁.

или .

.

С₁ можно определить из начальных условий:

р^/ = у^/ = 1 при х = 1, следовательно, С₁ = 0, следовательно, .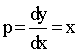

dy = xdx - отсюда .

Из начальных условий y = 0.5, следовательно, х = 1 и С₂ = 0.

Таким образом, .

Пример.

.

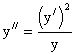- Первый случай

у^/ = р и . Подставим в уравнение, имеем

, следовательно, .

Отсюда

1) р = 0, то есть у=С

2) , следовательно, .

Далее

, то есть или .

Пример.

x×y^// = 2×x-y^/. (самостоятельно).

2.3. Линейные однородные уравнения второго порядка с постоянными коэффициентами

Пусть имеем линейное дифференциальное однородное уравнение

y^// + p×y^/ + q×y = 0. (2.8)

где p, q - постоянные коэффициенты.

Будем искать частное решение (2.8) в форме

у = е^kx, (2.9)

k = Const и ее нужно определить.

y^/ = k×e^kx и y^// = k×e^kx. Подставив эти выражения в (2.8), имеем

k²×e^kx + p×k×e^kx + q×e^kx º 0,

сокращая на еkx, имеем

k² + p×k + q = 0 (2.10)

- так называемое характеристическое уравнение.

З а м е ч а н и е. Для составления характеристического уравнения достаточно в уравнении (2.8) производные у^//, у^/ и саму функцию у заменить на соответствующие степени k.

Решив уравнение (2.10) получим

.

Имеем 3 случая:

1. , следовательно, имеем два действительных корня k₁ и k₂. Следовательно, (2.8) допускает два различных частных решения:

и ; если k₁¹k₂, то эти решения будут линейно независимы.

Определение. Два решения у₁ и у₂ называются линейно зависимыми, если можно подобрать постоянные числа а₁ и а₂, неравные одновременно нулю, такие, что линейная комбинация этих функций тождественно равна нулю, то есть

а₁×у₁ + а₂×у₂ º 0.

В противном случае (то есть если таких чисел подобрать нельзя) у₁ и у₂ называются линейно независимыми. Тогда общее решение данного уравнения есть линейная комбинация этих частных решений

.

2. , следовательно, .

В этом случае корень называется кратным, и частное решение будет одно:

.

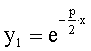Всякое другое частное решение у₁, линейно независимое с у₂, обязательно должно иметь вид

у₂ = у₂×z(x),

где z(x) - некоторая функция, не являющаяся константой.

.

.

.

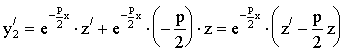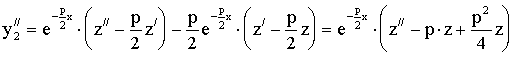Подставив эти выражения в (2.8), имеем

или

.

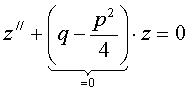Следовательно, z^// = 0.

Тогда z^/ = a и z = ax + b, где a и b - произвольные константы. И, следовательно,

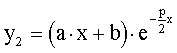. (2.11)

Если нам нужно только частное решение, то можно принять а=1,b=0 и тогда

То есть общее решение уравнения (2.8) во втором случае имеет вид

.

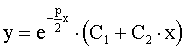3. , то будем иметь два сопряженных комплексных корня

k₁ = a + i×b и k₂ = a - i×b, где

и .

Таким образом, общее решение имеет вид

. (2.12)

Пример.

у^// - 6×у^/ + 9 = 0.

Характеристическое уравнение имеет вид

k² - 6×k + 9 = 0.

Решив его, имеем

, следовательно, .

Теорема 2.1. Пусть дано дифференциальное уравнение

у^//+ р×у^/+q×y = 0.

1. Если характеристическое уравнение имеет действительные корни k₁, k₂ такие, что k₁ ¹ k₂, то все решения имеют вид

2. Если характеристическое уравнение имеет равные действительные корни k=k1=k2, то решение имеет вид

3. Если характеристическое уравнение имеет мнимые корни k_1,2 = a ± i×b, (b ¹ 0), то

либо (2.12).

Эта теорема даст все решения уравнения (2.8).

Назад Далее