3

Понятие множества

Понятие множества является одним из основных в математике. Система, семейство, совокупность – эти термины можно считать синонимами слова «множество».

Множество – можно определить как совокупность объектов, объединенных по определенному признаку.

Например, множество зрителей в данном кинотеатре, множество студентов, совокупность коммерческих банков, имеющих уставный фонд не ниже 100 млн. грн. и т.д. Множество может содержать конечное или бесконечное число объектов.

Объекты, составляющие множество, называются его элементами, или точками множества.

Обычно множества обозначаются большими буквами, а входящие в них элементы – малыми буквами. Элемент из множества соответствует записи . Если же элемент не принадлежит множеству , то это соответствует записи .

Пусть и – два множества. Тогда между ними можно определить следующие соотношения.

1. Если оба множества состоят из одних и тех же элементов, то они совпадают, что соответствует записи .

2. Если все элементы множества содержатся в множестве , то говорят, что является подмножеством (или ).

3. Если ни один элемент множества не содержатся в множестве , то, значит, и само множество не содержится в (или ).

В математике используется понятие пустого множества, обозначаемого символом Æ. Это множество не содержит ни одного элемента и, поэтому, оно является подмножеством любого множества.

Введем понятие суммы множеств и их пересечения.

Суммой, или объединением, множеств и называется совокупность элементов, входящих как в множество , так и в множество . Обозначается объединение - .

Например, пусть - множество государственных предприятий с годовым оборотом не ниже денежных единиц, а - множество негосударственных предприятий с тем же нижним порогом годового оборота. Тогда будет множество всех предприятий с указанным нижним ограничением .

Пересечением множеств и (или их общей частью) называется совокупность одинаковых элементов, входящих как в множество , так и в множество . Обозначается пересечение - .

Отсутствие элементов со свойствами множеств и одновременно означает, что пересечение этих множеств - представляет собой пустое множество Æ.

Разностью множеств и называется множество , содержащее все элементы множества , не содержащиеся в ; эта разность обозначается - .

При записи математических выражений целесообразно употреблять математическую символику. Вместо выражения «любое из множества » употребляют запись , где перевернутая латинская буква " (квантор общности) взята от начала английского слова Any (любой). Аналогично, вместо выражения «существует элемент из множества » кратко записывают , где перевернутая латинская буква $ (квантор существования) является начальной буквой английского слова Existence – существование.

Даны множества и . Найти объединение, пересечение и разность множеств.

Очевидно, что объединение двух данных множеств , их пересечение -, а разность .

Множества, элементами которых являются действительные числа, называются числовыми множествами.

Из школьного курса алгебры известны множества - действительных чисел, - рациональных чисел, - иррациональных чисел, - целых чисел, - натуральных чисел.

Множество вещественных чисел является бесконечным. Оно состоит из рациональных и иррациональных чисел.

Рациональным называется число вида , где и - целые числа.

Всякое рациональное число является либо целым числом, либо представляет собой бесконечную десятичную периодическую дробь.

Иррациональное число представляет собой бесконечную десятичную непериодическую дробь.

Например, рациональное число можно представить в виде 0,1111111… , а иррациональное число .

Понятие функции.
Основные свойства функций

Постоянной величиной называется величина, сохраняющая одно и тоже значение.

Например, отношение длины окружности к ее диаметру есть постоянная величина, равная p.

Если величина сохраняет постоянное значение лишь в условиях данного процесса, то в этом случае она называется параметром.

Переменной называется величина, которая может принимать различные числовые значения.

Например, при равномерном движении S = vt, где путь S и время t – переменные величины, а v – параметр.

Если каждому элементу множества () ставится в соответствие вполне определенный элемент множества (), то говорят, что на множестве задана функция .

При этом называется независимой переменной (или аргументом), –зависимой переменной, а буква обозначает закон соответствия.

Множество называется областью определения (или существования) функции, а множество – областью значений функции.

Если множество специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной , т.е. множество таких значений , при которых функция вообще имеет смысл.

Например, область определения функции есть полуинтервал , так как ; если же переменная обозначает, предположим, время, то при естественном дополнительном условии областью определения функции будет отрезок .

Способы задания функций

Задать функцию – значит указать закон, по которому, согласно определению, каждому значению аргумента из области определения ставится в соответствие значение функции из области значений функций. Существует три основных способа задания функций: табличный, аналитический и графический.

Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента и соответствующие значения функции , например таблица логарифмов. Табличный способ имеет широкое применение в различных отраслях знаний и приложениях: ряды экспериментальных измерений, социологические опросы, таблицы бухгалтерской отчетности и банковской деятельности и т.п.

Аналитический способ состоит в задании связи между аргументом и функцией в виде формул. Этот способ наиболее часто встречается на практике. Так, функция , рассматриваемая выше, задана аналитически. Не следует смешивать функцию с ее аналитическим выражением. Так, например, одна функция

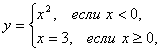
имеет два аналитических выражения, используемых при различных значениях аргумента.

Графический способ состоит в том, что соответствие между аргументом и функцией задается посредством графика. Этот способ обычно используется в экспериментальных измерениях и употреблением самопишущих приборов (осциллографы, сейсмографы и т.д.).

Основные свойства функции

1. Четность и нечетность. Функция называется четной, если для любых значений из области определения и нечетной, если . В противном случае функция называется функцией общего вида.

Например, функция является четной, а функция - нечетной. Функция является функцией общего вида, так как и и .

График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

2. Монотонность. Функция называется возрастающей (убывающей) на промежутке , если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

Пусть и . Тогда функция возрастает на промежутке X, если и убывает, если .