Модуль №3. Интегральное исчисление

Рекомендации

к самопроверке изученного материала

После изучения определенной темы по учебнику и решения достаточного количества соответствующих задач студенту рекомендуется воспроизвести по памяти определения, выводы формул, формулировки и доказательства теорем, проверяя себя каждый раз по учебнику.

В случае необходимости надо еще раз внимательно разобраться в материале учебника и решить задачи. Иногда недостаточность усвоения того или иного вопроса выясняется только при изучении дельнейшего материала. В этом случае надо вернуться назад и повторить плохо усвоенный раздел.

Важным критерием усвоения теории является умение решать задачи на пройденный материал. Однако здесь следует предостеречь студента от весьма распространенной ошибки, заключающейся в том, что благополучное решение задач воспринимается им как признак усвоения теории. Иногда правильное решение задачи получается в результате применения механически заученных формул без понимания сущности теоретических положений.

Темы:

3.1. Определение и свойства неопределенного интеграла

3.1.1. Первообразная и неопределенный интеграл

3.1.1.2. Неопределенный интеграл

3.1.1.3. Основные свойства неопределенного интеграла

3.1.1.4. Таблица простейших неопределенных интегралов

3.2. Методы интегрирования (основные)

3.2.1. Независимость вида неопределенного интеграла от выбора аргумента

3.2.2. Понятие об основных методах интегрирования

3.2.3. Интегрирование рациональных дробей с квадратным знаменателем

3.2.4. Интегрирование простейших иррациональностей

3.2.5. Интегрирование тригонометрических функций

3.2.6. Интегралы от некоторых трансцендентных функций

Вопросы для самопроверки:

· Сформулируйте определение первообразной функции. Докажите, что любые две первообразные одной и той же функции отличаются на постоянное слагаемое.

· Что называется неопределенным интегралом? Каков его геометрический смысл и основные свойства?

· Постройте кривые семейства y =∫xdx, проходящие через точки М₁(2; 1), М₂(2; 2), М₃(2; 3).

· Каковы основные методы интегрирования функций?

Практическое занятие №1

· Выведите формулу интегрирования по частям.

· Укажите целесообразные подстановки для отыскания интегралов:

Практическое занятие №2

3.3. Замечания об интегралах (не выражающихся через элементарные функции)

Повторим теорию

3.4. Определенный интеграл

3.4.1. Определение интеграла по Риману

3.4.2. Свойства определенного интеграла

3.4.3. Определенный интеграл с переменным верхним пределом

3.4.4. Формула Ньютона-Лейбница

3.4.5. Геометрический смысл определенного интеграла

3.4.6. Теорема о среднем для определенного интеграла

3.5. Методы вычисления определенного интеграла

3.5.1. Замена переменного

3.5.2. Интегрирование по частям

3.5.3. Приближенное вычисление определенного интеграла

3.5.4. Несобственные интегралы

3.6. Приложения определенного интеграла

3.6.1. Площадь плоских фигур

3.6.2. Объем тела вращения

3.6.3. Длина дуги

3.6.4. Дифференциал дуги

3.7. Понятие о кратных интегралах

3.7.1. Основные способы вычисления двойного интеграла

3.7.1.1. Вычисление площадей при помощи двойного интеграла

3.8. Понятие о тройном интеграле

Вопросы для самопроверки:

· Что называется интегральной суммой данной функции f(x) на данном отрезке [а; b]?

· Что называется определенным интегралом данной функции f(x) на данном отрезке [а; d]? Каковы его основные свойства и геометрический смысл?

· Напишите формулу Ньютона — Лейбница.

· В чем состоит способ подстановки и интегрирования по частям для вычисления определенного интеграла?

· Какие геометрические величины можно вычислять с помощью определенного интеграла? Напишите основные формулы и приведите примеры.

· Что называется несобственным интегралом с бесконечным пределом интегрирования?

· Какие из приведенных интегралов являются несобственными:

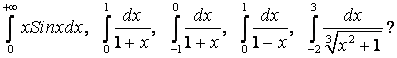
Какие из этих несобственных интегралов сходятся?

· Каков геометрический смысл несобственного интеграла?

· Может ли при вращении бесконечно протяженной кривой вокруг какой-либо прямой образоваться тело конечного объема? Рассмотрите пример кривой у = е^-х (0 < х < +∞), вращающейся вокруг оси Ох.

Повторим теорию

Внимание ! Правильно выбери свой вариант, например, если Ваш № зачетной книжки заканчивается цифрами ….51, то Ваш вариат 21.

Индивидуальные задания