Даны вершины треугольника А(-5; 1), В(2; 5), С(-3; -2).

                  Сделать чертеж и найти:

1)     периметр треугольника;

2)     уравнение высоты, проведенной через вершину С;

3)     уравнение прямой ЕС, проходящей через точку С и параллельной прямой АВ;

4)     уравнение медианы СМ, проведенной через вершину С;

5)     угол, который медиана ВМ₁, проведенная через вершину В, образует со стороной ВС;

6)     координаты точки К - пересечения медиан треугольника;

7)     площадь треугольника АВС;

Задание 2.

Составить уравнение геометрического места точек одинаково удаленных от точек А(0; 2) и от прямой х = 4. Построить кривую второго порядка.

М2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

Индивидуальные задания к модулю №2

Задание 3.  Найти пределы функций не используя правило Лопиталя:

Задание 4. Найти производные заданных функций:

у = ln(e-2x + xe-2x)

Задание 5. Найти пределы функций, используя правило Лопиталя:

Задание 6.  Вычислить приближенное значение , заменив в в точке х = х₀ приращение функции дифференциалом, если n = 7, a = 142,  х₀ = 128.

Задание 7. Исследовать средствами дифференциального исчисления функцию y = f(x) и построить ее график.

.

Задание 8. Найти экстремум функции двух переменных z = f(x,y):

z = x²- 4xy + y³ + 4x.

Задание 9. Выполнить лабораторную работу №1.

Цель работы: Нахождение параметров приближенной зависимости между величинами методом наименьших квадратов.

Xi	22	19	13	10	8	4	4	7	9	14
Yi	9,5	6,5	3,5	4	6	9	10	7	5,5	3

М3. Интегральное исчисление

Индивидуальные задания к модулю №3

Задание 10. Найти неопределенные интегралы. Результаты проверить дифференцированием.

a)

 

b).  Проинтегрировать по частям:

Задание 11. Вычислить по формуле Ньютона-Лейбница определенный интеграл:

Задание 12. Найти площадь фигуры, ограниченной кривой y = ax² + px + q и прямой y = kx + b:

Задание 13. Выполнить лабораторную работу №2.

Цель работы: Освоение методов численного интегрирования.

З а д а н и е:

1. Вычислить 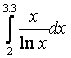приближенно, используя методы 2,3,4 по обобщенным

    формулам (5), (7), (9) с абсолютной точностью çR(f)ç £ 0,01.

2. Полученные результаты сравнить и сделать выводы.

    Используйте ЭВМ (например, Excel).

3. Постройте графики подынтегральных функций y = f(x).

М4. Дифференциальные уравнения

Индивидуальные задания к модулю №4

Задание 14. Найти общее решение дифференциального уравнения a(x)y' + b(x)y = f(x) и частное решение, удовлетворяющее начальному условию y = y₀ при x = x₀.

	y0 = 2	x0 = 0

Задание 15. Найти общее решение дифференциального уравнения ay" + by' + qy = f(x)  и частное решение, удовлетворяющее начальному условию y = y_0, y' = y'₀ при x = x₀.

3.

М5. Ряды  и  понятие о сходимости рядов

Индивидуальные задания к модулю №5

Задание 16. Выполнить лабораторную работу №3.

Цель работы: Исследование рядов на сходимость. Вычисления суммы ряда.

a). Исследовать на сходимость ряды:

• Вычислите чистую современную стоимость следующих потоков дохода:

а) =1000 гр. ежегодно и бессрочно (пожизненная рента) при ставке 5% годовых;

б) =1000 гр. ежегодно и бессрочно при ставке 12% годовых;

в) =1000000 гр. ежегодно и бессрочно при ставке 10% годовых;

г) =1000000 гр. ежегодно и бессрочно, но начиная с пятого года  (=5) при ставке 15% годовых.

 

b). Найти область сходимости степенного ряда и исследовать сходимость на концах интервала:

.

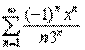Задание 17.

a). Разложить по степеням x в ряд y = f(x). Указать интервал сходимости.

b). Разложить в ряд Маклорена или Тейлора функцию y = f(x) в окрестности х₀:

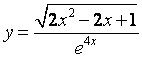  х₀ = 1.

М6. Линейная алгебра

Индивидуальные задания к модулю №6

Задание 18. Выполнить лабораторную работу №4.

Цель работы: Использование теории матриц и определителей для решения задач линейной алгебры.

З а д а н и е.    1. Решить систему линейных уравнений методом Крамера:

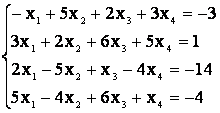
2. Проверить, что векторы

 образуют базис в R³, найти координаты вектора b в этом базисе. (Систему

 решать матричным методом или методом Гаусса).

М7. Элементы векторной алгебры

Индивидуальные задания к модулю №7

Задание 19. Даны точки A, B, C, D. Положим а = , b =.

Найти:

1) векторы 2а+b и а-2b;
2) модули векторов |2а+b| и |а-2b|;
3) скалярное произведение (2а+b)×(a-2b);
4) векторное произведение [(2а+b),(a-2b)];
5) угол между векторами (2а+b)×и (a-2b).

М8. ГЕОМЕТРИЧЕСКИЕ пространства

Индивидуальные задания к модулю №8

Задание 20. Даны четыре точки A, B, C и D:

1). Составить уравнение плоскости, проходящей

• через точку A и имеющей нормальный вектор ;

• через точки A, B, C.

2). Вычислить расстояние от точки D до плоскости, проходящей через точки A, B, C.

3). Составить канонические и параметрические уравнения прямых, проходящих через точки A и C, а также B и D.

4). Будут ли эти прямые перпендикулярны? Параллельны?